- •Д. Н. Цивинский Приложение метода возмущений к исследованию структуры потоков в аппаратах подготовки и транспорта нефти и газа
- •Д. Н. Цивинский Приложение метода возмущений к исследованию структуры потоков в аппаратах подготовки и транспорта нефти и газа
- •Метод возмущений
- •Обобщение методов возмущения
- •1. Физическая сущность применения трассеров при исследовании динамическиx xарактеристик потоков в каналах произвольной формы
- •2. Метод моментов
- •2.2. Распределение вероятностей случайной величины
- •2.3. Распределение частиц потока по времени пребывания в аппарате
- •2.4. Основные характеристики распределений
- •3. Анализ структуры потоков
- •3.1. Импульсное возмущение
- •3.1.1. Вычисление начальных моментов
- •3.1.2. Приведение переменных
- •3.1.3. Приведение начальных моментов
- •3.1.4. Вычисление центральных моментов
- •3.1.5. Приведение центральных моментов
- •3.2. Ступенчатое возмущение
- •4.1. Модель идеального смешения
- •4.2. Модель идеального вытеснения
- •4.3. Ячеечная модель
- •4.4. Диффузионные модели
- •4.5. Комбинированные модели
- •5. Примеры расчётов
- •5.1 Анализ структуры потоков по результатам испытания импульсным возмущением
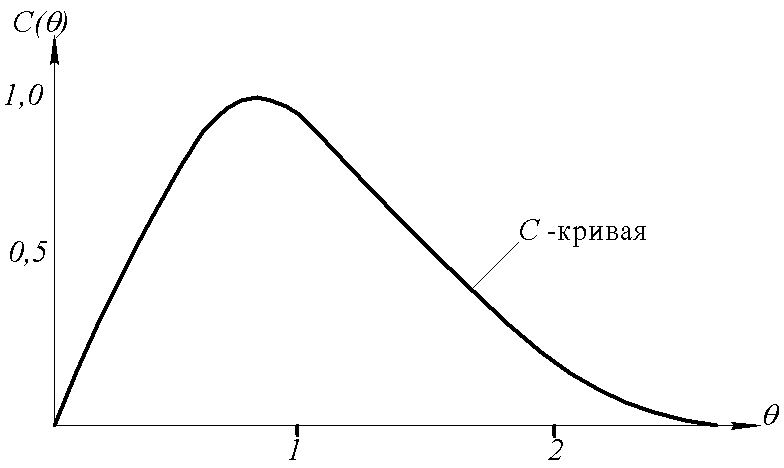
- •Построение c-кривой
- •Зависимость концентрации трассера от времени при импульсном возмущении и результаты расчётов
- •Расчёт характеристик структуры потоков в аппарате
- •Определение числа ячеек ячеечной модели
- •Определение коэффициента продольного перемешивания
- •5.2. Анализ структуры потоков по результатам испытания ступенчатым возмущением
- •Построение f-кривой
- •Зависимость концентрации трассера от времени
- •6. Определения некоторых терминов
Зависимость концентрации трассера от времени при импульсном возмущении и результаты расчётов
i |
01 |
02 |
03 |
04 |
05 |
06 |
07 |
08 |
|
|
0 |
300 |
600 |
900 |
1200 |
1500 |
1800 |
2100 |
|
|
0 |
849 |
1415 |
1415 |
1132 |
566 |
283 |
0 |
|
|
425 |
1132 |
1415 |
1274 |
849 |
425 |
142 |
0 |
5660 |
|
127 |
1019 |
2123 |
2674 |
2292 |
1401 |
552 |
- |
10188 |
|
3.82 |
71.3 |
242 |
424 |
466 |
348 |
162 |
- |
1717 |
|
1274 |
3396 |
4245 |
3821 |
2547 |
1274 |
425 |
- |
16980 |
|
3.44 |
138 |
745 |
1805 |
2538 |
2307 |
1267 |
- |
8802 |
|
1.03 |
85.3 |
726 |
2417 |
4435 |
4798 |
3105 |
- |
15466 |
|
0 |
0.5 |
0.83 |
0.83 |
0.67 |
0.33 |
0.17 |
|
|
|
0 |
0.45 |
0.75 |
0.75 |
0.60 |
0.3 |
0.15 |
|
|
|
0 |
1/3 |
2/3 |
1.0 |
4/3 |
5/3 |
2.0 |
7/3 |
|
Вычисляем безразмерную концентрацию по формуле

результаты вычислений заносим в табл.2.
Вычисляем параметрическую концентрацию по формуле (3.12) и параметрическое время по формуле:
![]()
Результаты вычислений заносим в табл.2 и строим график зависимости (рис.29).
Расчёт характеристик структуры потоков в аппарате
Осуществим приведение начальных моментов в параметрические координаты по формуле (3.16):
|
Рис.29. Кривая отклика проточного аппарата на импульсное
возмущение в параметрических координатах
|
![]()
![]()
![]()
Вычисляем
дисперсию
![]() по формуле (3.20):
по формуле (3.20):
![]()
Стандартное отклонение переменной равно
![]()
Вычисляем дисперсию по формуле (3.26):
![]()
Вычисляем третий центральный момент, характеризующий скошенность или асимметрию распределения по формулам (3.22) и (2.26):
![]()

Очевидно,
что коэффициент асимметрии, будучи
безразмерной характеристикой, не зависит
от того, приведены ли моменты
![]() и
и
![]() в параметрические координаты
в параметрические координаты
![]()

Вычисляем четвёртый центральный момент и эксцесс по формулам (3.23) и (2.28):
![]() ;
;

![]()
![]()