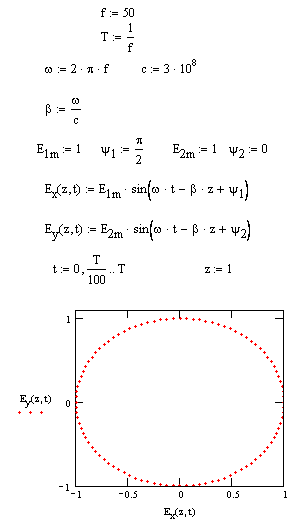- •В. И. Маненков, м. А. Польский
- •200900 «Сети связи и системы коммутации»,
- •201200 «Средства связи с подвижными объектами»
- •Практическая работа №1 Исследование движения заряженных частиц в электрических и магнитных полях
- •3. Движение заряженных частиц в электрическом и магнитном полях
- •Задания:
- •Практическая работа №2 Исследование электростатического поля при заданном распределении зарядов
- •Задания:
- •Практическая работа №3 Фурье анализ. Сложение колебаний и волн.
- •Задания:
- •Практическая работа №4 Исследование поляризационной структуры электромагнитного поля
- •Задания:
- •Практическая работа №5 Исследование волновых явлений на границе раздела двух диэлектриков
- •Задания:
- •Практическая работа №6 Распространение электромагнитных волн в прямоугольном волноводе
- •Задания:
- •Практическая работа №7 Распространение электромагнитных волн в цилиндрическом волноводе
Задания:
Для области размером 20×20:
Рассмотреть поле точечного заряда
 Кл.
Получить эквипотенциальные поверхности
и линии напряженности обычным способом
и с помощью уравнения Пуассона.
Кл.
Получить эквипотенциальные поверхности
и линии напряженности обычным способом
и с помощью уравнения Пуассона.Рассмотреть поле двух точечных зарядов
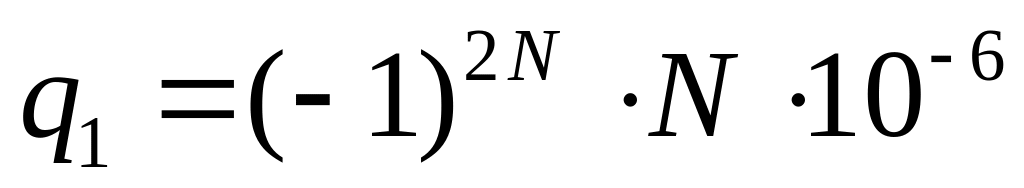 Кл и
Кл и
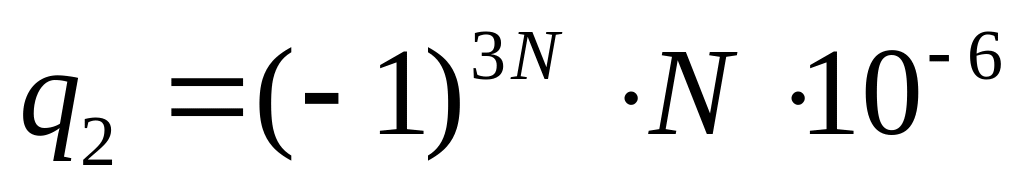 Кл. Получить
эквипотенциальные линии и линии
напряженности.
Кл. Получить
эквипотенциальные линии и линии
напряженности.Рассмотреть поле трёх точечных зарядов
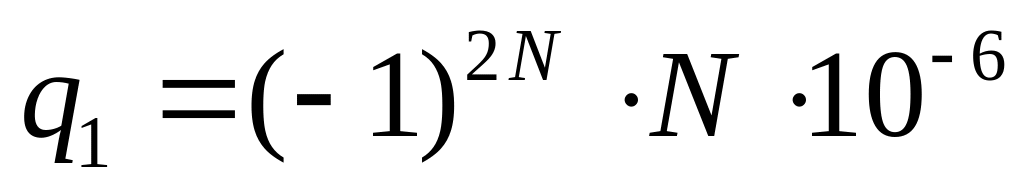 Кл,
Кл и
Кл,
Кл и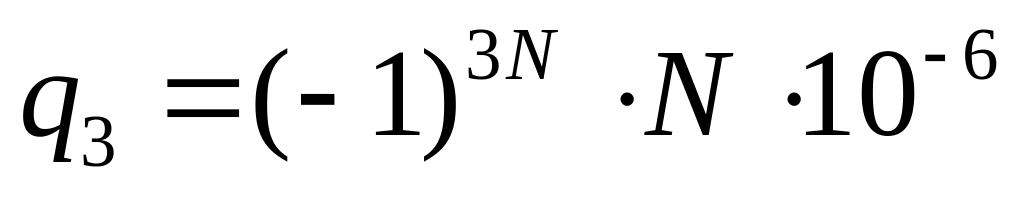 Кл. Получить
эквипотенциальные линии и линии
напряженности.
Кл. Получить
эквипотенциальные линии и линии
напряженности.
Для области размером 50×50:
Рассмотреть поле заряженной пластины
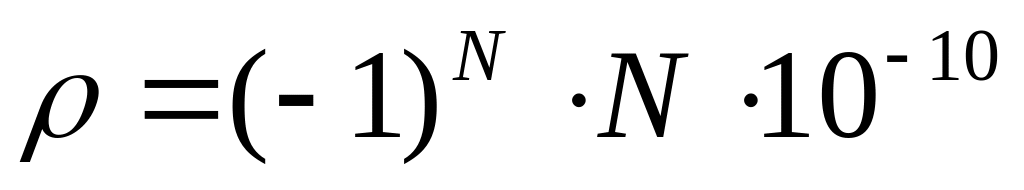 .
Получить эквипотенциальные линии и
линии напряженности.
.
Получить эквипотенциальные линии и
линии напряженности.Рассмотреть поле двух параллельных заряженных пластин
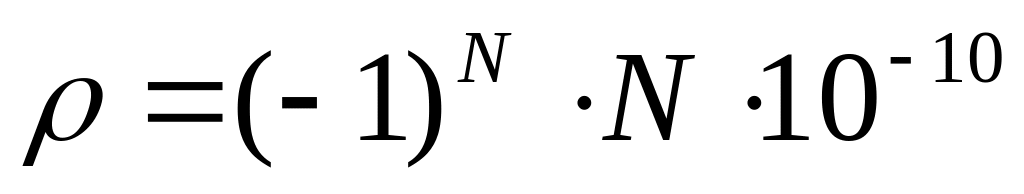 и
и
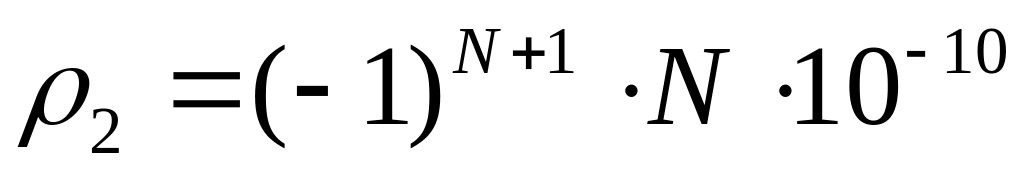 .
Получить эквипотенциальные линии и
линии напряженности.
.
Получить эквипотенциальные линии и
линии напряженности.
Здесь N – номер варианта
Практическая работа №3 Фурье анализ. Сложение колебаний и волн.
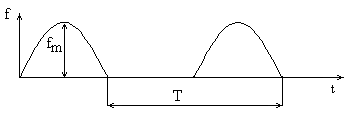
Рассмотрим сигнал, изменяющийся во времени по произвольному закону (рис.3.1). Если мгновенные значения сигнала повторяются через равные промежутки времени, сигнал называется периодическим.
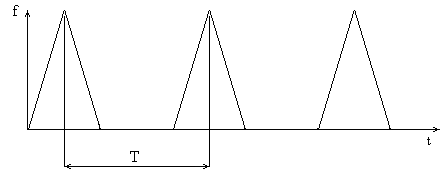
Рисунок 3.1 Пилообразный сигнал
Любую периодическую функцию f(t), удовлетворяющую условиям Дирихле, можно разложить в гармонический ряд Фурье:
![]() ,
(3.1)
,
(3.1)
где
![]() – частота
основной (первой) гармоники сигнала;
– частота
основной (первой) гармоники сигнала;
![]() –
частоты второй, третьей и гармоник более
высокого порядка (n
= 2, 3, 4 …);
–
частоты второй, третьей и гармоник более
высокого порядка (n
= 2, 3, 4 …);
![]() –
постоянная составляющая сигнала;
–
постоянная составляющая сигнала;
![]() –
амплитуды косинусоидальной и синусоидальной
составляющих сигнала.
–
амплитуды косинусоидальной и синусоидальной
составляющих сигнала.
Коэффициенты разложения определяются соотношениями:
![]() ;
;
![]() ;
;
![]() .
.
Выражение (3.1) можно записать в виде:
![]() ,
(3.2)
,
(3.2)
где
![]() ;
;
![]() .
.
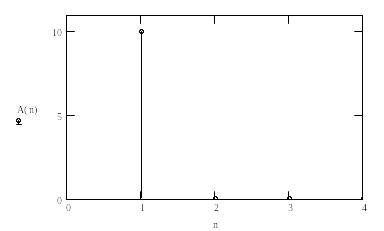
Правую часть (3.2) на оси частот можно показать в виде линий амплитудного спектра f(t) и фазового спектра f(t) (рис. 3.2)
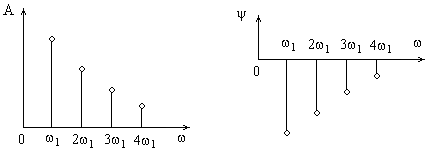
Рис. 3.2 Амплитудный и фазовый спектр f(t)
Пример 3.1. Определим амплитудный спектр косинусоидального сигнала с помощью пакета MathCAD
![]()
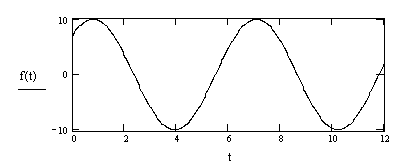
![]()
![]()
![]()
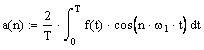
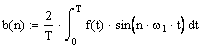
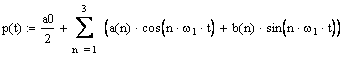
![]()
![]()
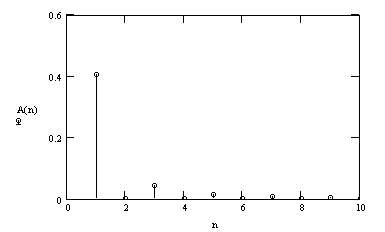
Пример 3.2. Разложим в ряд Фурье пилообразный сигнал и определим его амплитудный спектр:

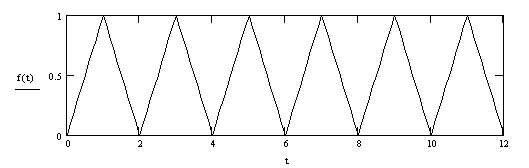
![]()
![]()
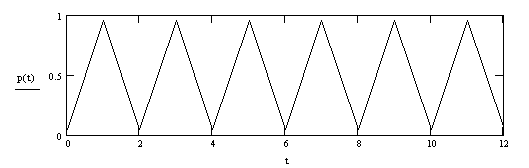
Пример 3.3. Разложим в ряд Фурье и определим амплитудный спектр сигнала последовательности прямоугольных импульсов:
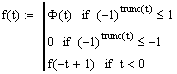
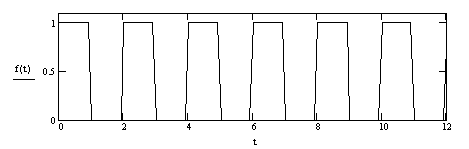
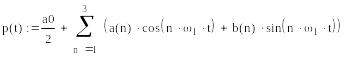
![]()
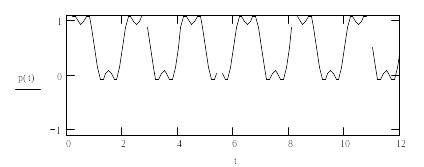
![]()
![]()
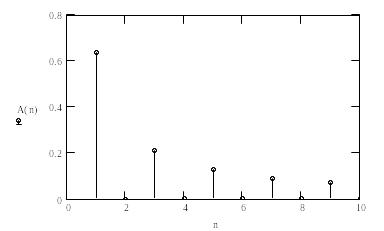
Задания:
Разложить в ряд Фурье и определить амплитудный спектр следующие сигналы:
1.

2.

3.
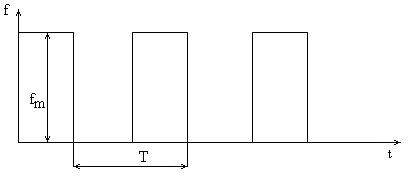
4.
fm = N; T = N, где N – номер варианта
Практическая работа №4 Исследование поляризационной структуры электромагнитного поля
Поляризация характеризует ориентацию вектора Е электромагнитной волны. Поляризацией плоской волны называют изменение значения и направления вектора Е в точке наблюдения за время Т.
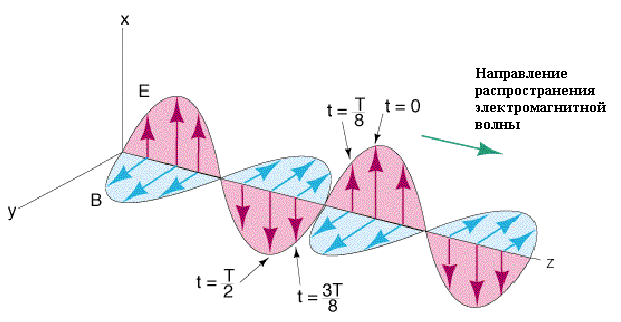
Рисунок 4.1
Виды поляризации:
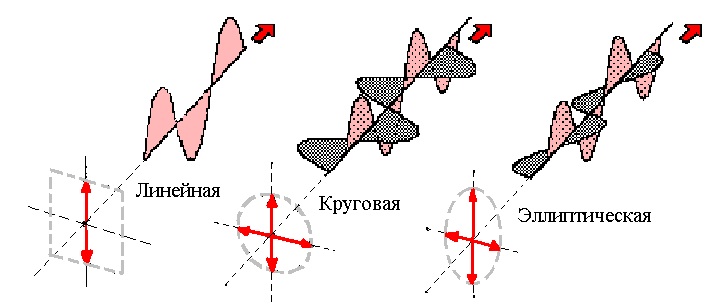
Рисунок 4.2
Линейная поляризация
В
случае произвольной ориентации вектора
![]() в
плоскости ХОY,
его можно разложить на 2 составляющие
Ex
и Ey:
в
плоскости ХОY,
его можно разложить на 2 составляющие
Ex
и Ey:
![]()
где
![]()
Подставив в уравнение плоской волны, получим:
![]() .
.
Длина
(модуль) вектора:
![]() .
Угол φ
– из выражения
.
Угол φ
– из выражения
![]() .
.
Наложение 2-х гармонических линейно поляризованных волн, векторы Е которых взаимно перпендикулярны, а фазы совпадают, дает линейно поляризованную волну.
Круговая поляризация
Рассмотрим 2 гармонические линейно поляризованные волны, электрические векторы которых взаимно перпендикулярны (ортогональны), а амплитуды и начальные фазы неодинаковые.
Решим совместно уравнения:
![]()
Получим уравнение эллипса:
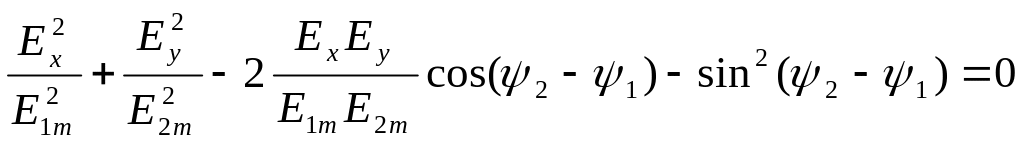
Пример 4.1 Круговая поляризация