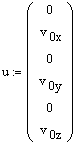АСТРАХАНСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

КАФЕДРА ЭЛЕКТРОТЕХНИКИ

В. И. Маненков, м. А. Польский

Методические указания к практическим занятиям по курсу

«Электромагнитные поля и волны»

для студентов очной и заочной

форм обучения специальностей:

200900 «Сети связи и системы коммутации»,

201200 «Средства связи с подвижными объектами»

Астрахань 2012 г.

Содержание	Стр.
Движение заряженных частиц в электрических и магнитных полях Электростатические поля при различном распределении зарядов Фурье анализ. Сложение колебаний и волн Поляризационная структура электромагнитного поля Волновые явления на границе раздела двух диэлектриков Электромагнитное поле в прямоугольном волноводе Электромагнитное поле в круглом волноводе. Рекомендуемая литература	3 10 15 20 22 24 29 34

Практическая работа №1 Исследование движения заряженных частиц в электрических и магнитных полях

1. Движение заряженных частиц в электрическом поле.

Предположим, что заряженные частицы, двигавшиеся параллельно оси X со скоростью попадают в однородное электрическое поле напряженностью E плоского конденсатора – рис 1.1. Направляя ось Y параллельно полю, имеем: E_X = E_Z = 0, E_Y = E.

Движение частиц в этом случае происходит под действием постоянной силы

, где q – заряд частицы.

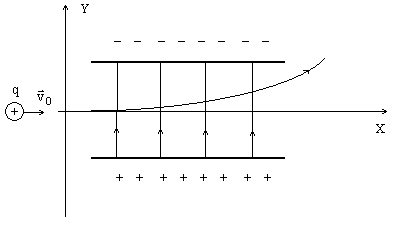
Рисунок 1.1

Уравнение движения , где , можно записать в виде системы уравнений

(1.1)

Систему дифференциальных уравнений (1.1) можно решать численным методом Рунге-Кутта. Метод Рунге-Кутта это численный метод, когда искомая функция получается в виде таблицы.

Пример 1.1. Определим траекторию движения электрона в однородном электрическом поле с помощью пакета MathCAD. Дано: напряженность электрического поля E = 10 В/м; заряд электрона q = 1,6·10^–19 Кл; масса m₀ = 1,7·10^–27 кг; скорость v₀ = 100 м/с.

В среде MathCAD эти данные имеют вид:

Решение системы дифференциальных уравнений (1.1) методом Рунге-Кутта четвёртого порядка, посредством функции rkfixed:

Сформируем вектор начальных условий:

Сформируем вектор первых и вторых производных:

Граничные точки интервала, на котором ищется решение

Количество точек, в которых ищется решение

Встроенная функция пакета MathCad для решения дифференциальных уравнений

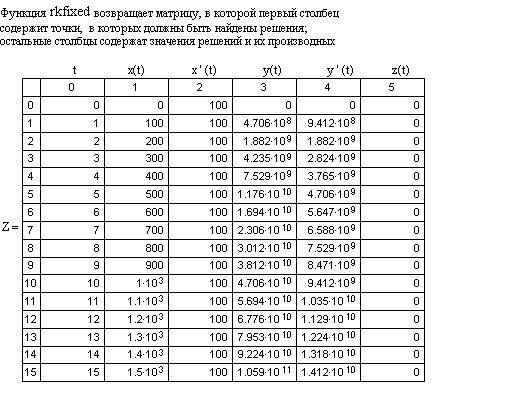
Функция

возвращает матрицу, в которой первый столбец содержит точки, в которых должны быть найдены решения; остальные столбцы содержат решения и их производные

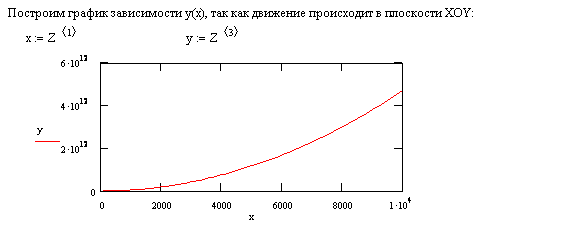
Траектория движения y(x) частицы в плоскости XOY

2. Движение заряженных частиц в магнитном поле

В постоянном магнитном поле на заряженную частицу действует сила

.

Эта сила перпендикулярна к скорости , а поэтому работы не производит, изменяя лишь траекторию движения частицы.

Рассмотрим случай однородного магнитного поля. Если скорость частицы направлена вдоль поля , то сила обратится в нуль, и частица будет двигаться равномерно и прямолинейно.

Если же частица движется перпендикулярно к магнит6ному полю, то её скорость оставаясь постоянной по величине, меняется по направлению. Сила также постоянна по величине и нормальна к траектории частицы. Следовательно, траектория частицы – окружность, плоскость которой перпендикулярна магнитному полю (рис.1.2). Направление вращения частицы зависит от знака заряда (магнитное поле направлено к читателю).

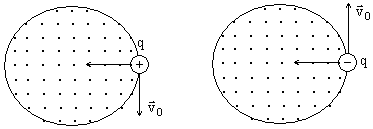
Рисунок 1.2.

Предположим, что заряженные частицы, двигавшиеся параллельно оси X со скоростью и попадают в однородное магнитное поле напряженностью B катушки с током.

Направляя ось Y параллельно полю, имеем:

В_X = В_Z = 0, В_Y = В.

Запишем уравнение движения

Т ак как , где то в проекциях на оси:

=> (1.2)

Пример 1.2 Определим траекторию движения заряда в однородном магнитном поле с помощью пакета MathCAD.

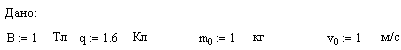
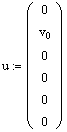
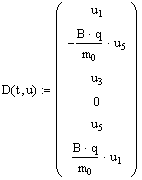
Граничные точки интервала, на котором ищется решение

Количество точек, в которых ищется решение

Встроенная функция пакета MathCad для решения дифференциальных уравнений

Траектория движения z(x) частицы в плоскости XOY

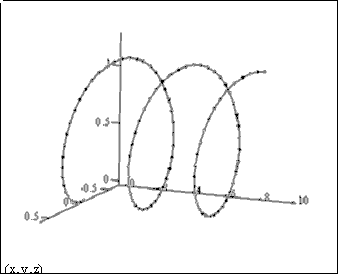
Пример 1.3 Рассмотрим движение заряженной частицы в однородном магнитном поле со скоростью, направленной под углом к вектору магнитной индукции.

Дано:

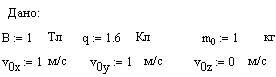
Векторы начальных условий и производных:

Граничные точки интервала, на котором ищется решение

Количество точек, в которых ищется решение

Встроенная функция пакета MathCad для решения дифференциальных уравнений

Траектория движения z(x) частицы в пространстве XYZ