5.3.2. Решение интегрального уравнения распространения световой волны в свободном пространстве

Покажем здесь, что интегральное уравнение распространения волн (5.10)

как и интегральное уравнение (преобразование) Фурье, обладает свойством обратимости, т.е. зная распределение поля E(x, y, z) в плоскости z = const > 0, можно найти спектр исходного распределения (в плоскости z = 0), а, следовательно, и само исходное распределение E(x, y, 0). Введем оптический фильтр с передаточной функцией

(9.23)

являющейся комплексно сопряженной передаточной функции слоя свободного пространства. Пусть распределение E(x, y, z) преобразуется указанным фильтром. Действие фильтра выразится в том, что функция спектральной плотности E(u, v) умножится на частотную характеристику фильтра и тогда вместо спектральной функции E(u, v) получаем спектральную функцию

E(u, v) = E(u, v) .

Подставляя это в уравнение (5.8)

,

получим

E(x, y, z) = =

= = E(x, y, 0).

Следовательно, действие фильтра, имеющего частотную характеристику вида (9.23), переводит выход во вход. Этого и следовало ожидать, так как комплексно сопряженной передаточной функции (9.23) соответствует комплексно сопряженная амплитуда плоской волны, которая описывает распространение волны в обратном направлении. Полученный результат и позволяет решить интегральное уравнение распространения волн вида (5.10).

Комплексно сопряженной передаточной функции соответствует, очевидно, и комплексно сопряженная импульсная характеристика. Для ее получения в любой формуле, определяющей импульсную характеристику слоя свободного пространства, следует заменить параметр z на – z (что соответствует замене i на – i). Тогда импульсная характеристика рассматриваемого фильтра будет иметь вид

h (x, y) =

(9.24)

– в общем случае или

h (x, y) = 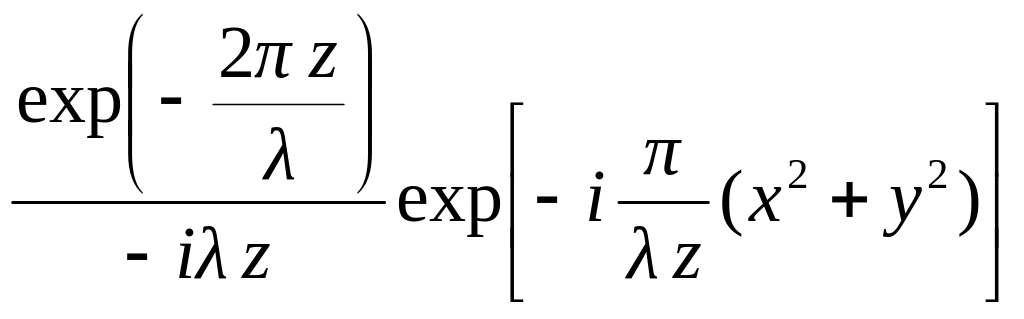(9.25)

– в приближении Френеля. Принимая распределение E(x, y, z) за входной сигнал, а распределение E(x, y, 0) за выходной, на основании интеграла суперпозиции получим

E(x, y, 0) = .

Подставляя сюда выражение (9.15), найдем E(x, y, 0):

E(x, y, 0) =

(9.26)

В приближении Френеля

E(x, y, 0) =

.

(9.27)

Соотношения (9.26) и (9.27) и решают задачу обратимости интегрального уравнения в представлении Рэлея: (9.26) – в общем случае, а (9.27) – в приближении Френеля.

5.4. Линейность оптической системы при различных видах освещения

Пусть в оптической системе, освещаемой когерентным светом, входным комплексным амплитудам и соответствуют выходные комплексные амплитуды и . Если система линейна, то комплексной амплитуде E₁(x, y) + + E₂ на входе должна соответствовать комплексная амплитуда на выходе. Выходная интенсивность будет при этом иметь вид многочлена:

(9.28)

где – выходная интенсивность при действии на входе только сигнала E₁, а – выходная интенсивность при действии только сигнала E₂. При когерентном освещении все четыре члена в (9.28), вообще говоря, не равны нулю. Следовательно, в этом случае система не линейна по интенсивности. Однако при некогерентном освещении выходная интенсивность складывается только из выходных интенсивностей: , т.е. системы, освещаемые некогерентным светом, линейны по интенсивности.

Различие между этими случаями является фундаментальным и составляет основу обсуждения процесса образования изображения, рассматриваемого в главах 11 и 12.

Рис. 9.3

Рассмотрим теперь оптическую систему (рис. 9.3), состоящую из протяженного источника света S, транспаранта T, расположенного в плоскости XY, оптической системы формирования изображения (на рисунке показана в виде прямоугольного параллелепипеда с входным и выходным отверстиями) и выходной плоскости (плоскости изображения) XY. Разобьем мысленно источник света на элементарные излучатели площадью d. Пусть – комплексная амплитуда поля в плоскости непосредственно перед транспарантом, обусловленного элементарными источниками света. Если функция пропускания транспаранта по амплитуде , то комплексное световое поле в плоскости непосредственно за транспарантом будет E(x, y) = E₀(x, y)t(x, y). Предположим, что оптическая система линейна, пространственно-инвариантна и имеет пространственную импульсную характеристику Тогда комплексное световое поле в выходной плоскости XY, обусловленное элементарным источником, можно описать уравнением свертки

E (x, y ) = E(x, y)h(x, y; x, y) = E₀(x, y)t(x, y)

h(x, y; x, y ). (9.29)

Интенсивность в выходной плоскости от элементарного источника света

dI′ (9.30)

а полная интенсивность в выходной плоскости, создаваемая всем источником света, будет

I′ = , (9.31)

где интегрирование проводится по всей площади  источника света S. Выражение (9.31) можно записать в виде интеграла свертки

, (9.32)

где

Г(x, y; x₁, y₁) =

представляет собой функцию взаимной пространственной когерентности. Эта функция характеризует статистическую связь полей в плоскости предмета. В параксиальном приближении функция определяется соотношением (4.25).

Г(x, y) ,

где I_S ( ) – интенсивность источника света, приходящаяся на единицу площади его поверхности на единичном расстоянии от него,   – координаты в плоскости источника света.

Рассмотрим два предельных случая.

1. Источник света пренебрежимо мал, т.е. I_S( ) =  ( ). В этом случае

Г(x y) = C₁, (9.33)

где C₁ – положительная постоянная. Функция взаимной пространственной когерентности Г отлична от нуля для любой пары точек в плоскости предмета. Этот случай соответствует полностью пространственно когерентному освещению (или, как говорят, полностью когерентной оптической системе), так как в этом случае имеет место статистическая связь между полями в плоскости предмета. Такое освещение можно получить от точечного источника света, расположенного в фокусе собирающей линзы без аберраций, поставленной перед транспарантом. С этой целью можно использовать и пучок лазерного излучения, который, как известно, обладает хорошей пространственной когерентностью даже при искусственном расширении пучка. В этом случае транспарант освещается коллимированным пучком света, т.е. плоской волной. Распределение поля в плоскости непосредственно за транспарантом будет пропорционально его функции пропускания по амплитуде t(x, y). При полностью когерентном освещении

I′

=

= E (x, y )E^(x, y ). (9.34)

Отсюда получаем

E (x, y ) = , (9.35)

где E(x, y) пропорционально t(x, y) – распределение комплексной амплитуды в предметной плоскости. Следовательно, в случае полностью когерентного освещения оптическая система линейна по комплексной амплитуде. При этом комплексная амплитуда на выходе определяется сверткой комплексной амплитуды на входе с импульсной характеристикой системы.

2. Источник света бесконечно большой, а его излучение однородно, т.е. I_S( ) = const. В этом случае функция взаимной пространственной когерентности

Г(x, y) = C₂ (x, y), (9.36)

где C₂ – комплексная постоянная. Это означает отсутствие статистической связи между полями точечных источников в плоскости предмета. Значение функции Г(x, y) отлично от нуля лишь в точках (x, y), поэтому выражение (9.36) соответствует полностью некогерентному освещению (описывает полностью некогерентную оптическую систему формирования изображения). Такое освещение можно получить от протяженного источника с помощью подходящего коллиматорного устройства. Следовательно, в случае полностью некогерентного освещения распределение интенсивности в выходной плоскости записывается в виде

I′

или

I′ . (9.37)

Стоящая в подынтегральном выражении (9.37) функция называется функцией пропускания транспаранта по интенсивности. Она будет пропорциональна распределению интенсивности поля в предметной плоскости I(x, y). С учетом этого интеграл (9.37) можно переписать в виде

или

I′ . (9.38)

Здесь . Функцию называют импульсной характеристикой оптической системы по интенсивности, некогерентной переходной функцией оптической системы, а также функцией рассеяния точки (сокращенно ФРТ). Эта функция описывает распределение интенсивности в изображении светящейся точки. Поскольку представляет интерес лишь относительное распределение интенсивности I, оказывается удобным нормировать ФРТ на единицу, т.е. положить

. (9.39)

Таким образом, в случае полностью некогерентного освещения интенсивность поля в выходной плоскости представляет собой свертку интенсивности входного сигнала с импульсной характеристикой системы по интенсивности. В случае полностью некогерентного освещения оптическая система является линейной относительно интенсивности.

В отличие от когерентного сигнала некогерентный сигнал описывается не комплексной, а действительной функцией. Эта функция несет информацию, заложенную в интенсивности световой волны. Следовательно, некогерентный сигнал несет только амплитудную информацию; фазовая информация утрачивается.

Таким образом, полностью когерентная оптическая система является линейной по амплитуде, а полностью некогерентная – по интенсивности. Общее выражение (9.32) соответствует частично-когерентному освещению.

Используя коммутативное свойство свертки, получим другое, более удобное, выражение для интенсивности поля в выходной плоскости:

. (9.40)