
- •Глава 10
- •3.2. Существование электромагнитных волн
- •9.2. Волновое уравнение электромагнитных волн
- •9.3. Плоская гармоническая электромагнитная волна
- •9.3.1. Формула плоской электромагнитной волны
- •9.3.2. Поляризация плоской электромагнитной волны
- •9.4. Сферические световые волны
- •9.4. Динамические характеристики электромагнитной волны
- •9.4.1. Энергия световой волны. Вектор Умова – Пойнтинга
- •9.4.2. Импульс электромагнитной воны
- •9.4.3. Момент импульса электромагнитной волны
- •9.5. Излучение электромагнитных волн
- •9.6. Шкала электромагнитных волн
Глава 10
ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ
3.2. Существование электромагнитных волн
Из и уравнений Максвелла вытекает, что переменное электрическое поле порождает магнитное поле, а переменное магнитное поле порождает поле электрическое. Поэтому если в какой-либо точке пространства возбудить с помощью колеблющихся электрических зарядов переменное электрическое поле, то это поле породит в соседних точках магнитное поле, которое тоже окажется переменным. Переменное магнитное поле в свою очередь породит в соседних точках переменное электрическое поле и т.д. Возникнет последовательность взаимных превращений электрического и магнитного полей, распространяющихся от одной точки пространства к другой. Такой процесс оказывается периодическим во времени и в пространстве, т.е. имеет волновой характер. Процесс распространения колебаний электрического и магнитного полей в пространстве называется электромагнитной волной.
Чтобы убедиться в том, что существование электромагнитных волн вытекает из уравнений Максвелла, покажем, что эти уравнения носят волновой характер. Для этого рассмотрим однородную электронейтральную (𝜌 = 0), непроводящую (j = 0) среду, характеризующуюся постоянными значениями электрической 𝜀 и магнитной μ проницаемостями. Для такой среды система уравнений Максвелла (8.21) – (8.24) примет вид
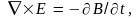 (9.1)
(9.1)
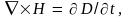 (9.2)
(9.2)
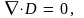
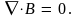 (9.3)
(9.3)
Выберем
декартову систему координат XYZ
и будем предполагать для простоты, что
векторы E
и B
поля зависят только от одной координаты
z.
При этом будем считать, что вектор E
колеблется вдоль оси X,
а вектор B
вдоль оси Y.,
т.е. что
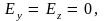 а
а
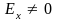 и
и
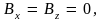 а
а
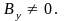 В этом случае система уравнений Максвелла
упрощается. Остаются только два уравнения.
Из уравнения (9.1) получаем
В этом случае система уравнений Максвелла
упрощается. Остаются только два уравнения.
Из уравнения (9.1) получаем
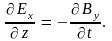 (9.4)
(9.4)
Аналогично из уравнения (9.2) получаем
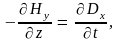
или
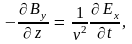 (9.5)
(9.5)
где
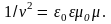
Уравнения (9.4) и (9.5) связывают друг с другом пространственные и временные производные полей и показывают, что изменение во времени одного поля приводит к изменению в пространстве другого поля и наоборот. Во времени и пространстве разыгрывается процесс взаимопревращения электрического и магнитного полей.
Легко убедиться, что если положить
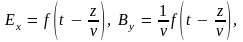
где
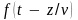 – произвольная функция аргумента
– произвольная функция аргумента
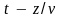 ,
то равенства (9.4)
и (9.5) обращаются в тождества. Следовательно,
система уравнений (9.4) и (9.5) имеет волновое
решение – описывает волну, распространяющуюся
вдоль оси Z
со скоростью
,
то равенства (9.4)
и (9.5) обращаются в тождества. Следовательно,
система уравнений (9.4) и (9.5) имеет волновое
решение – описывает волну, распространяющуюся
вдоль оси Z
со скоростью
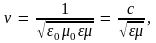 (9.6)
(9.6)
где
учтено, что
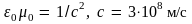 – скорость света в вакууме. Мы видим,
что электромагнитное поле может
существовать само по себе без зарядов
и токов. Такое поле не является статическим,
а представляет собой электромагнитную
волну. Взаимные превращения полей и
приводят к их сохранению.
– скорость света в вакууме. Мы видим,
что электромагнитное поле может
существовать само по себе без зарядов
и токов. Такое поле не является статическим,
а представляет собой электромагнитную
волну. Взаимные превращения полей и
приводят к их сохранению.
Таким образом, из уравнений Максвелла вытекает, что меняющийся во времени электромагнитный процесс, возникающий в одном месте, вызывает его изменение в другом месте с некоторым запаздыванием. Тем самым устанавливается конечность скорости распространения электромагнитных возмущений, а следовательно, и существование электромагнитных волн, распространяющихся в пространстве с конечной скоростью v.
Для
вакуума
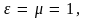 следовательно, скорость электромагнитных
волн в вакууме равна скорости света в
вакууме: v
= c.
На основании этого факта Максвелл пришел
к выводу, что свет (макроскопически)
представляет собой электромагнитную
волну.
следовательно, скорость электромагнитных
волн в вакууме равна скорости света в
вакууме: v
= c.
На основании этого факта Максвелл пришел
к выводу, что свет (макроскопически)
представляет собой электромагнитную
волну.
Тот
факт, что компоненты полей
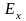 и
и
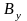 оказываются отличными от нуля при
нулевых значениях других компонент
свидетельствует от ом, что электромагнитная
волна является поперечной. Это означает,
что в электромагнитной волне векторы
электрического E
и магнитного B
полей колеблются перпендикулярно друг
другу и перпендикулярно направлению
распространения волны, причем вектоы
E,
B
и вектор скорости v
образуют правую тройку векторов.
оказываются отличными от нуля при
нулевых значениях других компонент
свидетельствует от ом, что электромагнитная
волна является поперечной. Это означает,
что в электромагнитной волне векторы
электрического E
и магнитного B
полей колеблются перпендикулярно друг
другу и перпендикулярно направлению
распространения волны, причем вектоы
E,
B
и вектор скорости v
образуют правую тройку векторов.
Из соотношений (9.4) и (9.5) вытекает связь между модулями электрического и магнитного векторов:
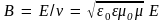 (9.7)
(9.7)
Это соотношение показывает, что в электромагнитной волне взаимно перпендикулярные векторы колеблются в одинаковой фазе (синфазно), они одновременно обращаются в нуль и одновременно достигают максимальных значений. Соотношение (9.4) справедливо как для текущих, так и амплитудных значений E и B.
