5.9. Зонная теория примесных полупроводников

Обсудим сначала изложенный в п. 4.2 процесс образования примесных полупроводников в терминах зонной теории. Кристалл, содержащий примеси, хаотически распределенные по его кристаллической решетке, уже не является идеальным, а представляет собой неупорядоченную систему. При малых концентрациях примесей в таких полупроводниках возникают кроме запрещенных и разрешенных энергетических зон так называемые локальные примесные энергетические уровни. Они образованы атомами примеси, а электроны (или дырки), находящиеся на этих уровнях, локализованы в пространстве каждый около «своего» атома примеси. И в отличие от свободных электронов (дырок) в разрешенных энергетических зонах, они не могут перемещаться по кристаллу и переносить электрический заряд, т.е. не дают вклад в проводимость, не перейдя в разрешенную зону. Такая локализация электронных (дырочных) состояний на примесных уровнях обусловлена, главным образом, тем, что атомы примеси хаотически распределены по решетке кристалла и при малых концентрациях они расположены весьма далеко друг от друга. Эти обстоятельства делают практически невозможным туннелирование электронов (дырок) между примесными атомами, приводя к локализации этих электронов (дырок) в окрестности примесных атомов. При достаточно большой концентрации примесей могут возникать новые разрешенные зоны, называемые примесными.

В случае полупроводников n-типа локальные примесные уровни называются донорными. Они расположены вблизи дна зоны проводимости, будучи отделены от нее небольшим энергетическим зазор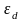ом (рис. 5.а). В случае полупроводников p-типа примесные уровни называются акцепторными. Они расположены вблизи потолка валентной зоны (рис. 5, б), будучи отделены от нее небольшим зазором 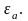Величина 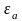обычно много меньше ширины запрещенной зоны

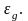
Отметим, что уровень Ферми в примесном электронном полупроводнике лежит (при не слишком высокой температуре) между нижним краем зоны проводимости и донорным уровнем (рис. 5., б). При некоторой достаточно высокой температуре уровень Ферми переходит к середине запрещенной зоны, и примесный полупроводник превращается в собственный.

При абсолютном нуле температуры (Т = 0) в полупроводнике n-типа валентная зона и донорные уровни полностью заполнены электронами, а зона проводимости пуста (рис. 5.). В полупроводнике p-типа при Т = 0 валентная зона полностью заполнена электронами, акцепторные уровни и зона проводимости пусты (рис. 5.).

Рассмотрим теперь механизм электропроводности примесных полупроводников на языке зонной теории.

При T > 0 в полупроводниках n-типа идут, вызванные тепловым движением, переходы электронов с донорных уровней в зону проводимости – тепловая генерация «примесь-зона», а также переходы электронов из валентной зоны в зону проводимости – генерация «зона-зона» (стрелки 1 и 2 на рис. 5.). Однако вероятности этих двух процессов тепловой генерации электронов в зону проводимости существенно различны. Для того, чтобы перебросить электрон с локального донорного уровня в зону проводимости, нужно сообщить ему дополнительную энергию, равную ширине энергетического промежутка 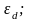для того, чтобы перебросить электрон с верхних уровней валентной зоны в зону проводимости, электрону необходимо сообщить гораздо большую энергию, равную ширине запрещенной зоны А поскольку вероятность таких переходов пропорциональна больцмановскому множителю 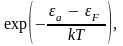где ε_а – энергия, требуемая для соответствующего перехода, то существенно различны будут и вероятности таких переходов:

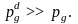(5.)

Идут и обратные переходы – процессы рекомбинации электронов проводимости с локализованными на донорных уровнях дырками и дырками, находящимися в валентной зоне. В состоянии теплового равновесия средние скорости прямых процессов – генерации и обратных процессов – рекомбинации равны друг другу. В результате чего и устанавливается некоторое стационарное распределение электронов по энергиям.

При комнатных температурах ситуация в полупроводнике n-типа такова. В зоне проводимости имеются свободные электроны, подавляющая часть которых в силу неравенства (5.) заброшена туда с донорных уровней и лишь незначительная их часть из валентной зоны. На донорных уровнях и в валентной зоне имеются дырки, суммарное количество которых равно количеству свободных электронов в зоне проводимости (так как электроны в зоне проводимости и дырки возникают и исчезают парами):

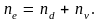(5.а)

Здесь n_e – концентрация электронов проводимости, n_d – концентрация дырок на донорных уровнях (равная концентрации ионизованных доноров), n_v – концентрация дырок валентной зоны. При этом подавляющая часть дырок, в силу того же неравенства (5.), находится на донорных уровнях, т.е.

n_d >> n_v. (5.б)

Однако дырки на донорных уровнях локализованы, и, следовательно, не могут переносить электрический заряд в пространстве, а значит, и участвовать в создании электрического тока. Дырки же валентной зоны являются свободными носителями электрического заряда и участвуют в создании электрического тока. Но, как следует из (5.а) и (5.б), концентрация n_e свободных электронов зоны проводимости много больше концентрации n_v свободных дырок валентной зоны:

n_e >> n_v (5.в)

и наличие свободных дырок практически можно не учитывать. Следовательно, электропроводность полупроводника с донорными примесями в рассматриваемой области температур (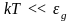 ) определяется лишь электронами проводимости (проводимость n-типа). При этом, как видно из (5.а) и(5.б), концентрация свободных электронов зоны проводимости практически равна при Т = 300 К концентрации дырок n_d, локализованных на донорных уровнях:

n_e = n_d.

В области же высоких температур, таких, что kT > ε_d равновесная концентрация свободных электронов зоны проводимости, как и при комнатных температурах, устанавливается в результате конкуренции процессов термической генерации электронов проводимости с донорных уровней и из валентной зоны и обратных ему процессов рекомбинации. Однако в области высоких температур происходит «истощение» донорных уровней, заключающееся в том, что все донорные примеси уже ионизованы и не могут при увеличении температуры дополнительно поставлять электроны в зону проводимости. При этом основным механизмом поставки электронов в зону проводимости становится их генерация из валентной зоны, так как концентрация донорных примесей много меньше концентрации основных атомов, хотя вероятность генерации с донорных уровней p_d больше вероятности генерации из валентной зоны p_g. Таким образом, и в этом случае выполняется равенство (5.а). Но теперь n_v >> n_d, а значит, n_e = n_v, т.е. концентрация свободных электронов зоны проводимости практически равна концентрации свободных дырок валентной зоны. И мы имеем практически такую же ситуацию, как и в собственном полупроводнике.

Итак, в примесном полупроводнике n-типа концентрация свободных электронов зоны проводимости определяется двумя отмеченными выше типами переходов: с донорных уровней и из валентной зоны. Поэтому его удельная электропроводность может быть представлена в виде суммы двух слагаемых, каждое из которых имеет активационный характер с энергией активации 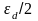и

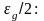
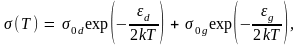(5.)

где коэффициенты 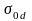и слабо зависят от температуры. В области комнатных температур определяющим в этом равенстве является первое слагаемое, а в области более высоких температур, когда наступает примесное истощение, – второе. Поэтому в координатах 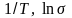график температурной зависимости удельной электропроводности примесного полупроводника будет иметь вид ломаной линии, в соответствии с преимущественным вкладом первого или второго слагаемого в данной области температур (рис. 5.).

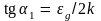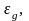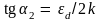В области высоких температур угловой коэффициент прямолинейного участка 1 определяется шириной запрещенной зоны как и в собственном полупроводнике, и поэтому эта область называется областью собственной проводимости. В области достаточно низких температур ( участок 2 на рис. 5) угловой коэффициент определяется шириной энергетического промежутка между донорными уровнями и зоной проводимости, и эта область называется областью примесной проводимости.

Для примесных полупроводников р-типа все рассуждения проводятся аналогично, если вместо электронов рассматривать дырки. Естественно, что и результаты, полученные таким способом, будут аналогичны тем, которые получены для полупроводников n-типа.