5.4. Квантовая теория электропроводности металлов

В классической электронной теории проводимости металлов была получена формула для удельной электропроводности (формула Друде (4.4)). Удельную электропроводность можно выразить и через среднюю длину свободного пробега 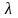электрона, если учесть, что 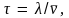где 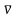– средняя арифметическая скорость теплового движения электрона. Тогда получим

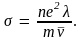(4.17)

Удельное сопротивление

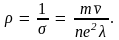(4.18)

При этом классическая электронная теория исходила из следующих предположений. Поведение электронов проводимости в металле аналогично поведению молекул идеального газа (т.е. пренебрегалось взаимодействием электронов друг с другом). Их распределение по скоростям и энергиям определялось статистикой Максвелла – Больцмана. Электроны совершают беспорядочное тепловое движение, причем их средняя тепловая скорость определяется так же, как и для молекул идеального газа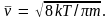 При создании в металле электрического поля возникает упорядоченное движение (дрейф) электронов, т.е. электрический ток. Существование средней длины свободного пробега связано со столкновением электронов с узлами кристаллической решетки.

Как и классическая, квантовая теория электропроводности исходит из того, что электропроводность металлов обусловлена внешними валентными электронами атомов. Эти электроны обладают подвижностью в металлическом кристалле. В модели сильной связи подвижность валентных электронов связывается с перекрыванием атомных волновых функций. Вследствие плотной упаковки атомов в металле перекрывание волновых функций значительно, поэтому электроны получают возможность переходить от атома к атому. Вероятность перехода определяется степенью перекрывания волновых функций, и чем она больше, тем больше и вероятность перехода. Вследствие этого в идеальном кристалле при T = 0 K электроны могут свободно перемещаться по кристаллу, не испытывая столкновения с ионами в узлах решетки. Их длина свободного пробега определялась бы лишь размерами образца.К такому же выводу можно придти и исходя из приближения почти свободных электронов. Согласно этому приближению стационарное состояние электрона в периодическом поле ионной решетки весьма похоже на состояние свободного электрона. Если состояние свободного электрона характеризуется значением импульса 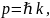состояние электрона в периодической решетке характеризуется значением квазиимпульса . Таким образом, инвариантность пустого пространства при бесконечно малом сдвиге (трансляции) обусловливает существование сохраняющейся векторной величины – импульса частицы. (Именно поэтому стационарное состояние электрона в пустом пространстве можно задавать значением импульса p.) Инвариантность кристалла при сдвиге на произвольный его период, приводит к появлению сохраняющегося вектора 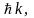очень похожего на импульс и называемого квазиимпульсом.

Исходя из квантовых представлений о волновых свойствах микрочастиц, электрон в металле должен рассматриваться как волна, и именно волновые свойства определяют его поведение в кристалле. В соответствии со сказанным о квазиимпульсе движение электрона в кристалле, подобно движению свободного электрона, можно рассматривать как распространение по кристаллу плоской волны с волновым вектором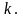 Эта плоская волна охватывает области кристаллической решетки, значительно превосходящие межатомные расстояния. Следовательно, электрон в своем движении в каждый момент времени не находится в окрестности какого-либо атома решетки, и существует некоторая вероятность его обнаружения в пространстве, окружающем другие атомы. Любой атом в таких условиях не является существенной преградой на пути направленного движения электрона. При движении электрона через строго периодический кристалл квазиимпульс сохраняется так же, как сохраняется импульс при свободном движении.Поэтому электрон в решетке со строго периодической потенциальной энергией (в идеальной решетке) движется не рассеиваясь на атомах, находящихся в узлах решетки. Влияние решетки кристалла на электрон сводится к изменению его массы. Это означает, что движение электрона в идеальном кристалле (без дефектов) можно считать полностью свободным, если вместо обычной массы электрона ввести так называемую эффективную массу 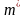. Эффективная масса может быть как больше, так и меньше массы 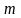свободного электрона. Для большинства металлов эффективная масса

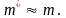
Плоская волна, описывающая движение электрона, распространялась бы по идеальному кристаллу без рассеяния, отражения и поглощения, кристалл был бы прозрачным для электрона. Этим объясняется факт беспрепятственного движения электрона через кристалл. Длина свободного пробега электрона в идеальном кристалле была бы бесконечной, а удельное сопротивление,равным нулю.

Причиной появления конечного значения длины свободного пробега электрона, а значит, и конечного электрического сопротивления являются всевозможные нарушения идеальности решетки, нарушения периодичности в расположении атомов, вызывающие искажения периодичности ее потенциала, на которых происходит рассеяние электронных волн и ослабление направленного потока электронов. К таким нарушениям относятся точечные дефекты (вакансии и атомы в междоузлиях), примеси инородных атомов, дислокации, границы зерен и просто тепловые колебания ионов в узлах. Они и обусловливают рассеяние электронных волн в реальном кристалле. При этом роль того или иного процесса рассеяния электронов на величину сопротивления зависит от области температур. При температурах, близких к абсолютному нулю, когда точечные дефекты практически отсутствуют, а тепловые колебания решетки несущественны, основное значение имеет рассеяние электронов на ионизированных атомах примеси. Рассеяние состоит в том, что ионы примеси отклоняют электроны, проходящие вблизи них, и тем самым уменьшают скорость их движения в первоначальном направлении. С этим рассеянием, а также с рассеянием на оставшихся дефектах и на так называемых нулевых колебаниях атомов кристалла и связано остаточное удельное сопротивление металла 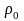приТ = 0 К. В области высоких температур основное значение имеет рассеяние электронов на тепловых колебаниях решетки – фононах. Фононы – это кванты энергии, отвечающие элементарным упругим волнам, распространяющихся в кристалле при тепловом возбуждении.

Каждый атом решетки совершает беспорядочные колебания около своего положения равновесия, оставаясь в пределах сферы с радиусом, равным амплитуде колебаний 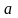. Площадь поперечного сечения этой сферы, равную 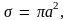можно принять за сечение рассеяния 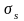колеблющегося атома: электрон, проходя через проводник и попадая в один из таких дисков, будет испытывать рассеяние. Средняя длина свободного пробега электрона , связанная с рассеянием на тепловых колебаниях будет ~ 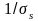~ 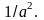Энергия гармонически колеблющегося атома пропорциональна квадрату амплитуды колебаний ~ 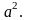С другой стороны, в соответствии с теоремой о равнораспределении энергии по степеням свободы средняя энергия атомов, совершающих тепловые колебания в твердом теле при 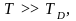где 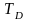– температура Дебая, пропорциональна температуреТ: ~ Т. Поэтому в области высоких температур средняя длина свободного пробега электронов, обусловленная рассеянием на тепловых колебаниях решетки, должна быть обратно пропорциональна температуре тела: ~ ~

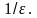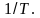
На рис. 2. в пространстве скоростей изображены две сферы Ферми – до и после включения электрического поля. Резкие границы сфер характерны для низких температур. Сфера Ферми до включения поля симметрична относительно начала координат. Это указывает на то, что количество электронов в проводнике, движущихся в противоположных направлениях, всегда одинаково, а их средняя скорость в любом направлении равна нулю. Этим и объясняется тот факт, что в проводнике, содержащем сколь угодно большое количество свободных электронов, электрический ток не возникает. Влияние внешнего поля на распределение электронов по состояниям сводится к смещению всего распределения (всей сферы Ферми) на величину, равную скорости дрейфа 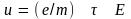в направлении, противоположном полю E. Вследствие этого распределение электронов по состояниям перестает быть симметричной относительно начала координат, и средняя скорость в направлении, противоположном полю E, уже не будет равна нулю, как в отсутствие поля. Сфера Ферми под действием поля смещается (сносится полем – дрейфует) как целое в направлении, противоположном внешнему полю E. Из рис. 2 видно, что квантовые состояния, расположенные левее энергии Ферми заняты электронами. В пространстве скоростей все эти состояния лежат внутри сферы Ферми радиуса 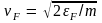. Поэтому внешнее поле может воздействовать только лишь на электроны, расположенные вблизи уровня Ферми, переводя их на более высокие свободные уровни путем переброски их из левой области распределения в правую. Это означает, что в формировании электропроводности в металлах могут участвовать не все свободные электроны, а лишь те из них, которые расположены непосредственно у уровня (границы) Ферми. Поэтому вместо средней скорости теплового движения в формулах (2.пр) и (2.сопр) следует взять скорость Ферми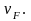 Во всех остальных отношениях механизм электропроводности и вид формул для 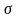и 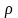не отличается от классического. Таким образом,

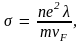
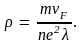
Основываясь на предположении о том, что электроны проводимости – вырожденный газ, подчиняющийся статистике Ферми– Дирака, Зоммерфельд получил следующую формулу для удельной электропроводности металлов

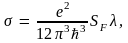
где S_F = 4𝜋k_F² – площадь поверхности сферы Фермисвободных электронов в k-пространстве с радиусом 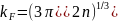. Формула Зоммерфельда получается из формулы Друде (4.4), если заменить в формуле (4.4) среднюю скорость vна скорость электрона на уровне Ферми v_F и учесть, что 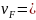ℏ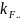 Если под S_F понимать площадь поверхности не сферы, а истинной ферми-поверхности, которая может существенно отличаться от сферы, то эта формула вполне годиться для расчета и анализа удельной проводимости металлов.

С помощью этого результата можно дать следующую физическую интерпретацию явления проводимости. Если выбрать разумное значение 𝜆, равное по крайней мере одному межатомному расстоянию, можно видеть, что проводимость пропорциональна площади поверхности Ферми. Следовательно, металлы с с большой площадью поверхности Ферми обладают высокой электропроводностью, в то время в изоляторах с нулевой площадью Ферми она равняется нулю. В такой трактовке позволяет объяснить явление проводимости как указанное выше смещение поверхности Ферми. Это происходит следующим образом. Так как для свободных электронов скорость 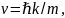уравнение движения электрона, находящегося на поверхности Ферми, под действием электрического поля Eимеет вид

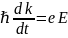
откуда следует, что в отсутствие столкновений сфера Ферми,не изменяя своей формы, будет смещаться в k-пространстве с постоянной скоростью. Интегрируя уравнение движения, получим

.

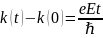Таким образом, если к заполненной сфере Ферми с центром в начале координат k-пространства приложить в момент времени t = 0электрическое поле, то попрошествии характерного времени 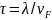центр сферы сместиться на величину

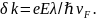
Вследствие столкновений электрона с примесями, дефектами решетки или вследствие тепловых колебаний решетки (что можно трактовать как столкновение с фононами – квантами колебаний решетки) сфера Ферми может стационарно сохранять свое смещенное положение при заданном электрическом поле. Если среднее время между столкновениями равно 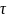, то стационарное в данном поле смещение сферы Ферми 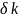определяется вышеприведенным выражением. Для приращения скорости 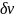имеем 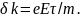С учетом этого плотность электрического тока, вызванного полем Eбудет равна

.

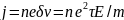Эта формула имеет форму закона Ома. Тем самым мы снова приходим к закону Ома и формуле Друде (4.4).

Длина свободного пробега𝜆, входящая в выражения для удельной электропроводности, есть мера эффективности столкновений электронов с препятствиями, мера рассеяния – длина, на которой, столкновения с вероятностью, близкой к единице, приводят к существенному изменению направления движения электронов. Ее часто называют транспортной длиной свободного пробега, подчеркивая тот факт, что эта величина входит в кинетические характеристики, описывающие явления переноса (транспортные явления). Когда имеется несколько независимых механизмов рассеяния, полная обратная длина свободного пробега определяется как сумма обратных длин пробега.

При рассеянии на примесях, вакансиях и междоузлиях длина свободного пробега от температуры не зависят. При рассеянии же на тепловых колебаниях решетки (фононах) ~ 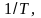и тогда, учитывая, что скорость 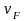не зависит от температуры, для удельного сопротивления при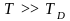 получим ~ T, что и наблюдается на опыте для указанной области температур. График зависимости 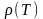показан на рис. 2. Видим, что в области высоких температур графиком функции является прямая, в области низких некоторая кривая (парабола пятой степени), вблизи абсолютного нуля – прямая , параллельная оси температур. 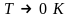Как видим, для нормальных металлов при удельное сопротивление принимает некоторое конечное значение 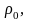неравное нулю.