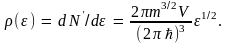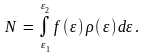- •Глава 5
- •5.1. Модель свободных электронов в металле
- •5.2. Зонный характер спектра электронов в твердых
- •5.4. Квантовая теория электропроводности металлов
- •5.5. Теплоемкость электронного газа
- •5.7. Термоэлектронная эмиссия
- •5.8. Зонная теория собственных полупроводников
- •5.9. Зонная теория примесных полупроводников
- •5.10. Контактные явления
Глава 5
ЭЛЕКТРОННЫЕ СОСТОЯНИЯ В ТВЕРДЫХ ТЕЛАХ
5.1. Модель свободных электронов в металле
В основе представлений о металлах лежит знание того факта, что при объединении в кристалл атомов металлов их валентные электроны отрываются от ядер и коллективизируются кристаллом, образуя электронный газ. Именно эти валентные электроны обеспечивают электропроводность металла и поэтому их называют электронами проводимости. Таким образом, металл – это ионная решетка, погруженная в электронный газ. Частицы (электроны) этого электронного газа необычно легки, а число их в единице объема – огромно. Эти два обстоятельства – малая масса m и большая плотность n – приводят к тому, что электронный газ является вырожденным (не подчиняется статистике Максвелла – Больцмана), проявляет квантовые статистические свойства. Электроны как частицы с полуцелым спином являются фермионами. Они подчиняются принципу Паули и описываются статистикой Ферми – Дирака.
Существует два приближенных метода расчета электронных состояний в кристаллах – приближения слабой и сильной связи. В приближении слабой связи (или приближении почти свободных электронов) в качестве нулевого приближения берутся волновые функции свободного электрона, а периодическое поле кристалла рассматривается как малое возмущение. В приближении сильной связи в качестве нулевого приближения выбираются волновые функции электрона в изолированном атоме, а взаимодействие между атомами, позволяющее электрону переходить от атома к атому, учитывается по теории возмущений. Приближение слабой связи хорошо описывает электроны проводимости в металлах.
В качестве нулевого (и тем не менее достаточно хорошего) приближения при описании электронного газа в металле принимается, что электроны не взаимодействуют между собой посредством кулоновских сил, т.е. считается, что они образуют идеальный ферми-газ (газ не взаимодействующих тождественных частиц, подчиняющихся статистике Ферми – Дирака). Энергетический спектр электронов в кристалле, как будет показано ниже, является дискретным. В случае дискретного энергетического спектра распределение Ферми – Дирака, как было показано в разделе «Статистическая физика и термодинамика», имеет вид
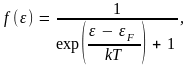 (5.5)
(5.5)
где
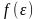 – вероятность того, что фермион находится
в состоянии с энергией
– вероятность того, что фермион находится
в состоянии с энергией
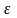 ,
,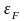 – константа (на самом деле имеет слабую
зависимость от температуры), называемая
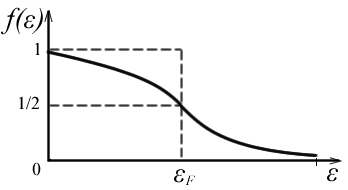
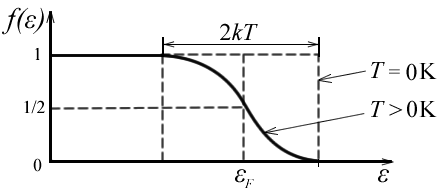
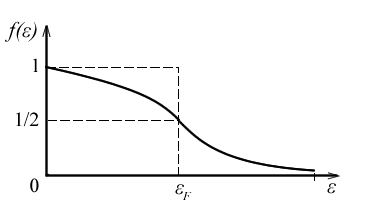
энергией (или уровнем) Ферми. График
этой функции показан на рис 4. При
– константа (на самом деле имеет слабую
зависимость от температуры), называемая
энергией (или уровнем) Ферми. График
этой функции показан на рис 4. При
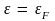 вероятность
вероятность
Рис. 4. |
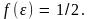 Следовательно,
уровень Ферми – это такой энергетический
уровень, вероятность заполнения которого
при любой температуре равна
Следовательно,
уровень Ферми – это такой энергетический
уровень, вероятность заполнения которого
при любой температуре равна
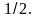
При T = 0 К функция (4.5) принимает вид
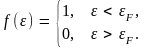
Видим, что при абсолютном нуле температуры все энергетические уровни вплоть до уровня Ферми заполнены электронами, а все уровни, расположенные выше уровня Ферми – пусты. Следовательно, уровень Ферми – это последний заполненный энергетический уровень при абсолютном нуле температуры. График этого распределения показан на рис. 4. пунктиром График имеет вид ступеньки (называемой фермиевской ступенькой) высотой, равной 1, и обрывающейся при .
При
низких температурах, т.е. когда
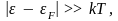 функцию (4.5) можно представить как
функцию (4.5) можно представить как
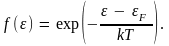 (5.6)
(5.6)
Энергетический спектр электронов в металле в приближении свободных электронов
Получим теперь в приближении свободных электронов спектр энергии электронов в металле. Рассмотрим макроскопический образец металла, который для простоты будем считать имеющим форму куба со стороной l. Для каждого отдельного электрона этот куб является трехмерной потенциальной ямой с бесконечно высокими стенками, поэтому уравнение Шредингера для свободного электрона внутри куба будет иметь вид
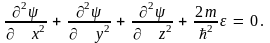 (4.7)
(4.7)
Решение этого уравнения будем искать в форме бегущей плоской волны
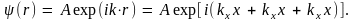 (4.8)
(4.8)
Постоянная A находится из условия нормировки
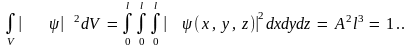
Откуда
получаем
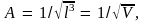 где
где
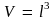 – объем образца. Следовательно,
– объем образца. Следовательно,
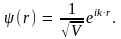
Подставляя
(4.4) в (4.3), находим связь между энергией
и волновым вектором k
(или импульсом
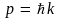 )
свободного электрона:
)
свободного электрона:
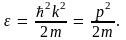 (4.9)
(4.9)
При выборе решения уравнения Шредингера в форме бегущих волн (4.4) удобно ввести так называемые периодические граничные условия, состоящие в том, что волновая функция должна быть периодической функцией по координатам x, y и z с периодом l, т.е.
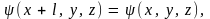 (4.10)
(4.10)
и аналогичные условия по координатам y и z. Условие (4.6) дает
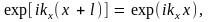 откуда
откуда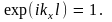 Это
равенство будет выполняться, если
Это
равенство будет выполняться, если
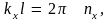 где
где
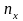 – целое число, и аналогично для других
компонент. Аналогично и для других
компонент. Следовательно, компоненты
волнового вектора k
будут определяться равенствами
– целое число, и аналогично для других
компонент. Аналогично и для других
компонент. Следовательно, компоненты
волнового вектора k
будут определяться равенствами
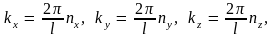 (.4.11)
(.4.11)
где
все целые числа
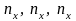 независимо друг от друга принимают
значения, равные
независимо друг от друга принимают
значения, равные
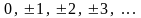
Таким образом, компоненты волнового вектора квантуются; при этом числа являются квантовыми числами. Тогда в соответствии с (4.5) квантоваться будет и энергия электрона. Подставляя в (4.5) соотношения (4.7), получаем собственные значения энергии состояний с волновым вектором k:
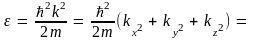
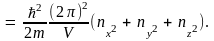 (4.12)
(4.12)
Квантовые
состояния электрона в этом приближении
определяются четырьмя квантовыми
числами (
и ms),
где ms
– квантовое число, определяющее проекцию
на какое-либо направление спина электрона
и принимающее значения
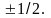 Компоненты
k
также можно рассматривать как квантовые
числа рассматриваемой задачи.
Компоненты
k
также можно рассматривать как квантовые
числа рассматриваемой задачи.
Как
видно из формулы (4.7), энергия электрона
зависит от суммы
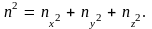 Данному значению суммы удовлетворяет
определенное число значений чисел
Данному значению суммы удовлетворяет
определенное число значений чисел
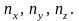 Другими словами, каждому значению суммы
n2
соответствует определенное значение
состояний электрона. Минимальному
значению энергии электрона (основному
уровню энергии) соответствуют значения
Другими словами, каждому значению суммы
n2
соответствует определенное значение
состояний электрона. Минимальному
значению энергии электрона (основному
уровню энергии) соответствуют значения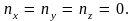 На этом уровне может находиться два
электрона с противоположными направлениями
спина
На этом уровне может находиться два
электрона с противоположными направлениями
спина
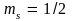 и
и
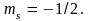 Этот уровень оказывается полностью
занятым электронами, поэтому третий
электрон системы должен занять уже
следующий – более высокий энергетический
уровень, так как в соответствии с
принципом Паули он не может находиться
на уже двукратно занятом основном
уровне. Энергетическому уровню, следующему
за основным (первому возбужденному
уровню), соответствует значение
Этот уровень оказывается полностью
занятым электронами, поэтому третий
электрон системы должен занять уже
следующий – более высокий энергетический
уровень, так как в соответствии с
принципом Паули он не может находиться
на уже двукратно занятом основном
уровне. Энергетическому уровню, следующему
за основным (первому возбужденному
уровню), соответствует значение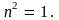 В этом случае числа
могут принимать значения 0
и
В этом случае числа
могут принимать значения 0
и
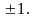 Такому значению суммы соответствует 6
комбинаций чисел
.
Поэтому с учетом двух значений квантового
числа
Такому значению суммы соответствует 6
комбинаций чисел
.
Поэтому с учетом двух значений квантового
числа
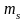 этот уровень имеет число состояний
(кратность вырождения)
этот уровень имеет число состояний
(кратность вырождения)
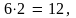 а
значит, на этом уровне может разместиться
12 электронов
с прямо противоположными направлениями
спинов. Второму возбужденному уроню,
соответствует значение
а
значит, на этом уровне может разместиться
12 электронов
с прямо противоположными направлениями
спинов. Второму возбужденному уроню,
соответствует значение
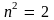 и, как
нетрудно убедиться, 12
комбинаций чисел
и 24 состояния.
Поэтому на этом уровне может разместиться
24 электрона и
т.д.
и, как
нетрудно убедиться, 12
комбинаций чисел
и 24 состояния.
Поэтому на этом уровне может разместиться
24 электрона и
т.д.
В соответствии с принципом минимума энергии электроны электронного газа при абсолютном нуле температуры будут последовательно заполнять все уровни с наиболее низкими значениями энергии, начиная с основного, пока не будут исчерпаны все электроны. При этом будут заполнены все уровни вплоть до некоторого уровня . Этот последний заполненный энергетический уровень при абсолютном нуле температуры представляет собой уровень (или энергию) Ферми .
Расчет энергии Ферми
Для
определения энергии Ферми введем в
рассмотрение пространство волнового
вектора (так называемое k-пространство),
по трем координатным осям которого
будем откладывать проекции
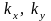 и
и
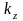 вектора k. В
этом пространстве каждому квантовому
состоянию электрона соответствует
точка. Поверхность равных значений
энергии (изоэнергетическая поверхность)
в этом пространстве описывается
уравнением
вектора k. В
этом пространстве каждому квантовому
состоянию электрона соответствует
точка. Поверхность равных значений
энергии (изоэнергетическая поверхность)
в этом пространстве описывается
уравнением
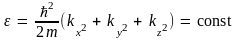
и имеет форму сферы, уравнение которой
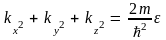 ,
,
а
радиус
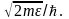
Квантовым
состояниям, энергия
которых не превышает значения энергии
Ферми
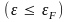 соответствует
объем шара ра-
соответствует
объем шара ра-
Рис. 4. |
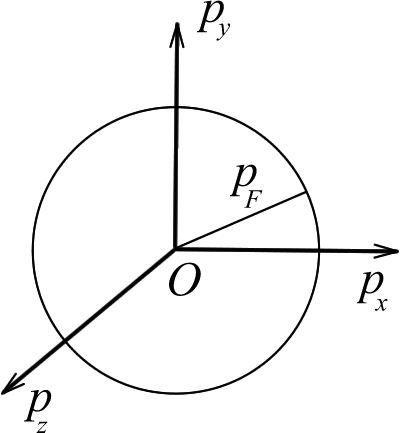
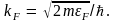 Сферическая поверхность указанного
радиуса называется сферой Ферми. В
импульсном пространстве сфера Ферми
Сферическая поверхность указанного
радиуса называется сферой Ферми. В
импульсном пространстве сфера Ферми
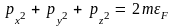 имеет
радиус
имеет
радиус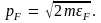 Эта сфера изображена на рис. 4.
Эта сфера изображена на рис. 4.
В
соответствии с определением абсолютного
нуля при Т = 0
К вся система электронов должна иметь
минимально возможную энергию. Поэтому
если бы электроны не подчинялись принципу
Паули, то все они должны были бы
расположиться в одном состоянии с
минимально возможной энергией, равной
нулю и с проекциями импульса т.е. в начале координат импульсного
пространства. Но в действительности
справедлив принцип Паули, не допускающий
одновременного нахождения в одном
состоянии более одного электрона с
определенным направлением спина. Поэтому
чтобы при Т = 0
К вся система электронов имела минимальную
энергию, в пространстве импульсов
электроны должны разместиться в
состояниях, расположенных максимально
близко к началу координат. Эти состояния
и заполняют объем шара конечного радиуса
(так как конечно число размещаемых
электронов), равного
т.е. в начале координат импульсного
пространства. Но в действительности
справедлив принцип Паули, не допускающий
одновременного нахождения в одном
состоянии более одного электрона с
определенным направлением спина. Поэтому
чтобы при Т = 0
К вся система электронов имела минимальную
энергию, в пространстве импульсов
электроны должны разместиться в
состояниях, расположенных максимально
близко к началу координат. Эти состояния
и заполняют объем шара конечного радиуса
(так как конечно число размещаемых
электронов), равного
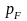 с
центром в начале координат.
с
центром в начале координат.
Поскольку
значения
и
квантованы в соответствии с (4.7), два
последовательных состояния будут
отличаться друг от друга значением
квантовых чисел
на 1: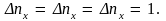 Поэтому
минимальные промежутки
Поэтому
минимальные промежутки
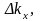
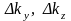 между последовательными значениями
волновых чисел (последовательными
состояниями) одинаковы и равны
между последовательными значениями
волновых чисел (последовательными
состояниями) одинаковы и равны
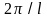 .
Это означает, что каждому квантовому
состоянию в этом k-пространстве
будет соответствовать не одна точка, а
целая ячейка в виде кубика со стороной
и объемом
.
Это означает, что каждому квантовому
состоянию в этом k-пространстве
будет соответствовать не одна точка, а
целая ячейка в виде кубика со стороной
и объемом
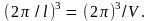 Все k-пространство,
таким образом, разделяется на кубические
ячейки указанных размеров, каждая из
которых соответствует одному состоянию.
Разделив объем шара, соответствующего
энергии состояний, не превышающей
значения энергии
,
Все k-пространство,
таким образом, разделяется на кубические
ячейки указанных размеров, каждая из
которых соответствует одному состоянию.
Разделив объем шара, соответствующего
энергии состояний, не превышающей
значения энергии
,
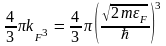
на
объем
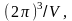 приходящийся
на одно состояние, найдем число состояний
с указанным значением энергии. Из-за
двух значений квантового числа
это число состояний следует увеличить
в два раза (следовательно, в каждой
ячейке может находиться два электрона
с противоположно направленными спинами).
Чтобы все состояния с энергией, не
превышающей энергию Ферми, были заполнены
электронами, число их должно быть равно
числу N электронов
в системе. Следовательно,
приходящийся
на одно состояние, найдем число состояний
с указанным значением энергии. Из-за
двух значений квантового числа
это число состояний следует увеличить
в два раза (следовательно, в каждой
ячейке может находиться два электрона
с противоположно направленными спинами).
Чтобы все состояния с энергией, не
превышающей энергию Ферми, были заполнены
электронами, число их должно быть равно
числу N электронов
в системе. Следовательно,
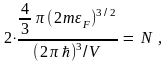
откуда
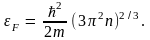 (4.13)
(4.13)
Здесь
n
– концентрация электронов. При характерных
для металлов концентрациях электронов,
n ~
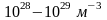 ,
получаем, что энергия Ферми
примерно равна нескольким электрон-вольтам.
Для натрия, например, где концентрация
электронного газа
,
получаем, что энергия Ферми
примерно равна нескольким электрон-вольтам.
Для натрия, например, где концентрация
электронного газа
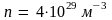 ,
энергия Ферми
,
энергия Ферми
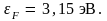 Энергия Ферми – это максимальное
значение энергии, которое могут иметь
электроны в металле при абсолютном нуле
температуры. Максимальная скорость
электронов при этом
Энергия Ферми – это максимальное
значение энергии, которое могут иметь
электроны в металле при абсолютном нуле
температуры. Максимальная скорость
электронов при этом
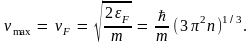
Эта
максимальная скорость электронов
оказывается очень большой, порядка
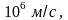 т.е. только на два порядка меньшей
скорости света.
т.е. только на два порядка меньшей
скорости света.
Как видим, движение электронов в металлах не прекращается и при абсолютном нуле температуры. Но движение это не является тепловым, это чисто квантовый эффект, обусловленный принципом Паули.
Если
повышать температуру, то часть электронов
за счет теплового движения будет
переходить из состояний с
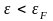 в состояния с
в состояния с
 При этом число электронов, перешедших
на более высокие уровни, равно количеству
образовавшихся свободных состояний в
области
.
Тепловая энергия
будет сообщаться вначале
При этом число электронов, перешедших
на более высокие уровни, равно количеству
образовавшихся свободных состояний в
области
.
Тепловая энергия
будет сообщаться вначале
только
электронам, имеющим энергию, непосредственно
примыкающую к уровню Ферми. Поэтому на
более высокие уровни энергии смогут
перейти только такие электроны, энергия
которых меньше энергии Ферми на величину
порядка
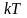
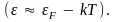 Электроны же, расположенные на более
глубоких уровнях, не изменяют своих
состояний. С повышением температуры
происходит размытие «фермиевской
ступеньки» в окрестности уровня Ферми,
и эта область размытия порядка 2
.
«Фермиевская ступенька» расплывается
и приобретает вид кривой, изображенный
на рис. 4. сплошной линией. При температуре
Электроны же, расположенные на более
глубоких уровнях, не изменяют своих
состояний. С повышением температуры
происходит размытие «фермиевской
ступеньки» в окрестности уровня Ферми,
и эта область размытия порядка 2
.
«Фермиевская ступенька» расплывается
и приобретает вид кривой, изображенный
на рис. 4. сплошной линией. При температуре
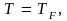 при которой
при которой
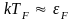 ,
она исчезает совсем. Определенная
равенством
,
она исчезает совсем. Определенная
равенством
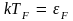 температура
температура
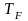 называется температурой Ферми.
называется температурой Ферми.
Таким
образом, при любых температурах все
энергетические
уровни, расположенные ниже уровня Ферми
заняты электронами, а все более высокие
– свободны. Между ними находится узкая
область шириной порядка 2
частично занятых состояний. Электроны,
заполняющие эту область, – и только они
– перераспределяются при различных
физических процессах. Отсюда ясно, что
в физике металлов важнейшую роль играют
электроны, энергия которых близка к
энергии Ферми. В k-пространстве
эти электроны располагаются вблизи
поверхности Ферми – поверхности
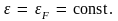
Плотность электронных состояний
Функция распределения Ферми – Дирака дает возможность определить вероятность заполнения тог или иного уровня энергии. Однако она не позволяет определить заселенность электронами данного интервала энергетических уровней. Для характеристики заселенности интервалов энергии вводится физическая величина, называемая плотностью электронных состояний ρ(ε). Она определяется как число состояний, приходящихся на единичный интервал энергий, т.е. ρ(ε) = dN′/dε, где N′ – полное число состояний, обладающих энергией ε. Состояния с квазиимпульсами от нуля до p в импульсном пространстве заполняют сферу радиуса p, поэтому это число равно
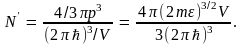
Продифференцировав это выражение по энергии , получим плотность состояний
|
(4.14) |
Видим, что эта функция имеет вид параболы, изображенной на рис. 4. Для металлов кривые распределения электронов при T = 0 К и T > > 0 К показаны на рис 4.
Зная функцию распределения f(ε) и плотность состояний ρ(ε), можно найти и число электронов, имеющих энергию в интервале от ε1 до ε2. Так как f(ε) – вероятность заполнения электроном одного состояния с энергией ε, то полное число электронов с энергией в интервале dε равно произведению функции f(ε) на число состояний ρ(ε)dε в данном интервале dε, а полное число электронов с энергией от ε1 до ε2, следовательно, будет
|
(4.15) |