11.6. Получение эллиптически поляризованного света

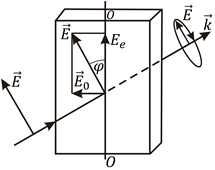
Двояко преломляющие кристаллы позволяют получить свет с круговой и эллиптической поляризацией. Рассмотрим случай, когда линейно поляризованный луч света падает нормально на поверхность двояко преломляющей пластинки, вырезанной параллельно оптической оси (рис. 11.9); направление колебаний вектора E луча составляет с оптической осью угол j. Пластинка разлагает луч на обыкновенный и необыкновенный. Амплитуды этих лучей зависят от ориентации вектора E относительно оптической

Рис. 11.9

оси, т.е. от угла j :

E_o = Esinφ, E_e = Ecosφ.

Оба луча пройдут через пластинку по одному и тому же направлению, но с различной скоростью и вследствие чего на выходе из пластинки между ними возникнет оптическая разность хода

и соответственно разность фаз

где l₀ – длина волны света в вакууме, – показатели пре-

ломления обыкновенного и необыкновенного лучей, d – толщина

Рис. 11.

пластинки. При выходе из пластинки колебания вектора E обеих волн складываются, и в зависимости от величин d и j будет наблюдаться тот или иной вид поляризации

Если толщина пластинки такова, что

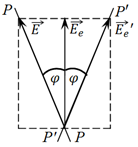
где m – целое число, то разность фаз на выходе между обыкновенным о и необыкновенным е лучами составит p. Поляризация останется линейной, но плоскость поляризации повернется на угол 2j относительно первоначальной ориентации. Действительно, при разности фаз между о- и е-лучами, равной p, на выходе из пластинки фазовое соотношение между указанными лучами будет соответствовать взаимному расположению векторов E_e и E_o¢, показанному на рис. 11.9. Поэтому свет, вышедший из пластинки, будет поляризован в плоскости Р¢Р¢, расположенной под углом 2j к плоскости РР. Пластинку такой толщины называют пластинкой в полволны. Минимальная толщина пластинки в полволны

При толщине пластинки, удовлетворяющей условию то и на выходе в зависи

мости от угла j получаем либо круговую (при когда амплитуды обыкновенного и необыкновенного лучей ), либо эллиптическую (при j, отличном от p / 4) поляризацию. Пластинку такой толщины называют пластинкой в четверть волны. Минимальная толщина такой пластинки

Эллиптическая поляризация получается и при толщине пластинки, отличной от указанных значений. Ориентация осей эллипса относительно оси ОО будет определяться разностью фаз и отношением амплитуд о- и е-лучей: т.е. углом j. Пропуская линейно поляризованный свет через две пластинки в четверть волны, снова получаем линейно поляризованный свет, но направление поляризации повернется на прямой угол.

11.7. Искусственная анизотропия. Эффект Керра

Рассмотренное выше двойное лучепреломление называется естественным, так как оно вызывается естественной анизотропией кристаллов. Но оптическая анизотропия материала может быть создана и искусственно с помощью различных внешних воздействий. Например, обычное стекло аморфно и изотропно. Но если подвергнуть кусок стекла одностороннему сжатию или растяжению, то он становится анизотропным и приобретает свойства двояко преломляющего кристалла.

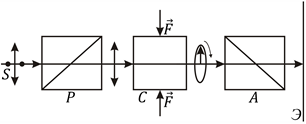
Рис. 11.11

Расположим стеклянную пластинку C между двумя скрещенными поляризаторами P и A (рис. 11.11); на поляризатор P направим луч естественного света от источника S. Так как стекло в нормальном (ненапряженном) состоянии не изменяет направления поляризации, то при скрещенных поляризаторах экран Э, расположенный за поляризатором А, не будет освещен. При сжатии (растяжении) стекла силой F возникает анизотропия; свет, выходящий из образца, оказывается эллиптически поляризованным и частично проходит через анализатор A – экран становится освещенным. Если деформация распределена по толще образца неравномерно, то неравномерной будет и освещенность, а при использовании белого света на экране появляется цветная, интерференционная картина, позволяющая судить о распределении деформаций (а, следовательно, и механических напряжений) в образце.

В качестве меры, возникающей анизотропии принимают разность показателей преломления обыкновенного и необыкновенного лучей: Опыт показывает, что эта величина пропорциональна механическому напряжению .

Рассмотренный эффект имеет практическое значение; он лежит в основе оптического метода исследования напряжений на прозрачных моделях. Модель конструкции изготовляют из прозрачного изотопного материала и подвергают нагрузке, пропорциональной той, которую будет испытывать реальная конструкция. Просвечивая модель поляризованным светом по схеме, показанной на рис. 11.11, можно определить внутренние напряжения в модели, а затем пересчитать их на проектируемую конструкцию.

Двойное лучепреломление в прозрачных диэлектриках можно получить и при воздействии электрического поля. Это явление но-

Рис. 11.12

сит название эффекта Керра. Его можно наблюдать, заменив в схеме на рис. 11.11 стеклянную пластинку С так называемой ячейкой Керра. Эта ячейка представляет собой герметический сосуд с жидкостью (обычно с нитробензолом), в который погружен конденсатор (рис. 11.12). При подаче на пластины напряжения нитробензол становится двояко преломляющим с оптической осью, ориентированной вдоль электрического поля E конденсатора, вследствие чего свет доходит до экрана Э. Возникающая в электрическом поле разность показателей преломления оказывается пропорциональной квадрату напряженности электрического поля E:

где k – коэффициент пропорциональности. Разность фаз приобретаемая обыкновенным и необыкновенным лучами на длине l конденсатора, будет равна

где – величина, называемая постоянная Керра.

Явление Керра объяснил Ланжевен. В сильном электрическом поле молекулярные диполи ориентируются преимущественно вдоль электрического поля, вследствие чего среда становится оптически анизотропной: световым волнам с поляризациями вдоль внешнего поля и перпендикулярно ему соответствуют различные значения показателей преломления.

Время, в течение которого устанавливается (при включении электрического поля) или исчезает (при выключении поля) преимущественная ориентация дипольных моментов молекул нитробензола, составляет примерно с. Поэтому ячейка Керра широко используется в качестве практически безынерционного затвора для световых лучей при сверхскоростных фотосъемках. С помощью ячейки Керра, питаемой напряжением высокой частоты, могут быть осуществлены прерыватели светового пучка (световые модуляторы) с частотой прерывания во много раз большей, чем у механических прерывателей с движущимися частями. Такие модуляторы применяются для управления режимом работы лазеров с целью получения сверхкоротких импульсов большой мощности.