11.4. Поляризация света при отражении и рассеянии

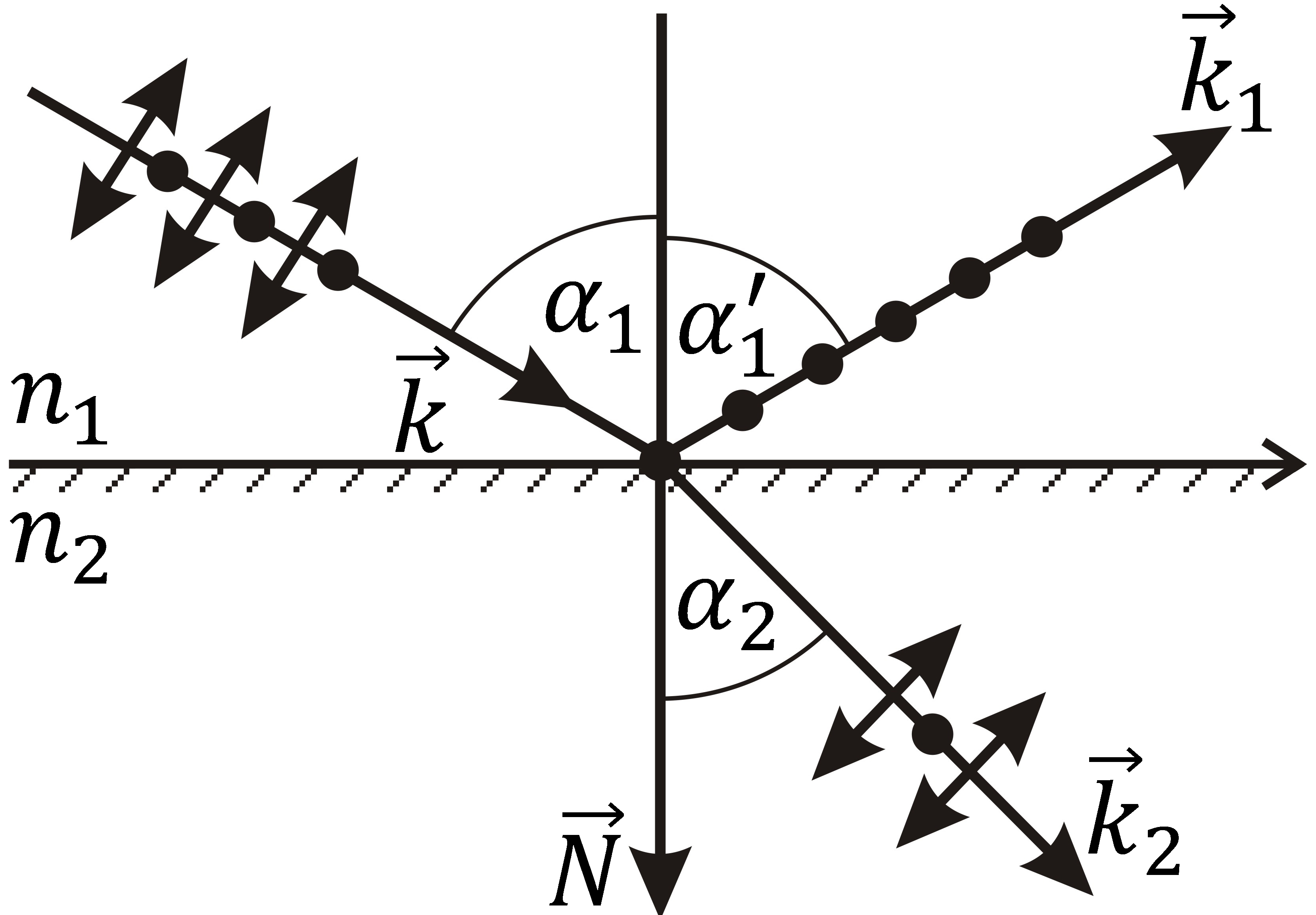
Линейно поляризованный свет можно получить при отражении от диэлектрика. Световой луч, отраженный от поверхности диэлектрика, оказывается полностью поляризованным перпендикулярно плоскости падения, если он перпендикулярен преломленному лучу (рис. 11.3, а). Действительно, если отраженный и преломленный лучи взаимно перпендикулярны, то

(11.5)

и тогда из первой формулы (14.12) следует, что амплитуда (E¢₁₀)_||, а значит, и интенсивность I¢_|| отраженной волны, поляризованной в плоскости падения, обращаются в нуль. Амплитуда же и интенсивность волны, поляризованной, перпендикулярно плоскости па-

Рис. 11.5

дения, как следует из первой формулы (14.13), при условии (15.5) в нуль не обращаются. Но падающую неполяризованную волну можно представить в виде двух не когерентных плоских волн: поляризованной в плоскости падения (параллельная составляющая) и в перпендикулярной ей плоскости (перпендикулярная составляющая). При выполнении условия (15.5) от поверхности раздела отразится только перпендикулярная составляющая, поэтому отраженный свет будет линейно поляризован перпендикулярно плоскости падения.

При условии (15.5) а так как то полная поляризация отраженной от диэлектрика волны будет иметь место при где

(11.6)

Так как при и то угол представляет собой уже упоминавшийся в п. 14. угол Брюстера. Для границы раздела воздух-стекло ( ) угол Брюстера Соотношение (15.6) называют законом Брюстера, а само явление полной поляризации отраженной волны при угле падения, равном углу Брюстера – явлением Брюстера.

Явление Брюстера можно объяснить исходя из молекулярной теории оптических явлений. Отражение света, как уже говорилось, есть результат интерференции вторичных волн, излучаемых молекулярными диполями диэлектрика, колеблющимися под действием электрического поля распространяющейся в диэлектрике преломленной световой волны. Так как колеблющийся диполь вдоль направления колебаний электромагнитных волн не излучает, то, ясно, что если электрическое поле преломленной волны колеблется параллельно отраженному лучу (что имеет место при ), то вызываемые ими колебания диполей не дают вторичных волн в направлении отраженной волны. Отраженная волна формируется вторичными волнами, возникающими вследствие колебаний диполей, а значит, и электрического поля преломленной волны, происходящих перпендикулярно плоскости падения. А поскольку поляризация волны, порождаемой колеблющимся диполем, совпадает с направлением его колебаний, то отраженная волна при угле падения, равном углу Брюстера ( ), оказывается поляризованной перпендикулярно плоскости падения. Преломленная волна при этом оказывается частично поляризованной с преимущественной поляризацией в плоскости падения. При угле падения, отличном от угла Брюстера ( ), отраженная и преломленная волны будут частично поляризованными.

Степень поляризации P можно определить с помощью формулы (15.2), положив в ней I_max = I_^, I_min = I_||. Для естественного света I_^ = I_|| и P = 0. Свет, отраженный под углом Брюстера, имеет I_|| = 0, и для него степень поляризации P = 0. Для преломленного света в случае естественного падающего света (когда [(E₀₁)_^] ² = = [(E₀₁) _||] ²) из формул Френеля (14.12) и (14.13) находим

I_^ / I_|| = [(E₀₂)_^] ² / [(E₀₂) _||] ² =

В этом случае I_|| ³ I_^, а - степень поляризации величина неположительная. Физически это и означает, что преломленный луч имеет преимущественную поляризацию в плоскости падения. Например, при падении естественного света под углом Брюстера на стеклянную пластинку преломленный луч имеет степень поляризации P = – 0,08. При прохождении через пластинку степень поляризации еще увеличится на 0,08. Расположив последовательно несколько пластинок (стопа Столетова), можно получить высокую степень поляризации света.

При отражении линейно поляризованного света от металла получается эллиптически поляризованный свет, если колебания электрического вектора E падающего луча направлены под углом к плоскости падения. Эллиптически поляризованный свет получается и при полном отражении.

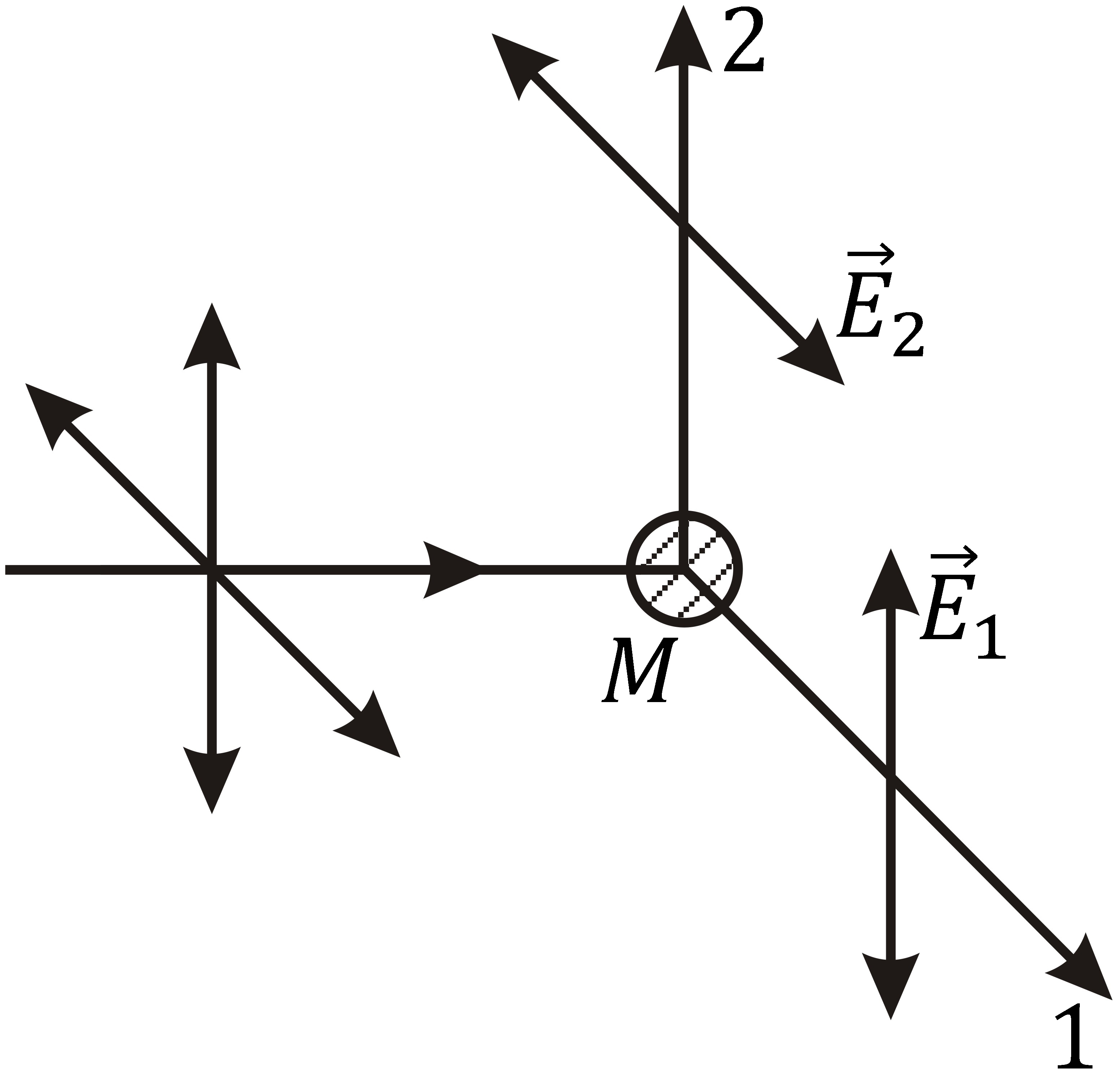
Рассмотрим теперь возникновение линейной поляризации света при рассеянии. На рис. 11.6 показана рассеивающая частица М,

Рис. 11.6

на которую падает неполяризованная световая волна. Под действием электрического поля этой волны дипольный момент частицы приходит в колебательное движение и создает вторичную (рассеянную) волну. Представим падающий естественный луч как некогерентную смесь двух волн одинаковой интенсивности, линейно поляризованных во взаимно перпендикулярных направлениях, например, в плоскости падения (плоскости рисунка) и перпендикулярно ей. Дипольный момент рассеивающей частицы также будет совершать колебания в этих направлениях. Колебания дипольного момента, происходящие в плоскости падения, создают рассеянный луч 1, который будет перпендикулярен плоскости падения и полностью поляризован в этой плоскости (поле E₁ на рис. 11.6). Колебания, происходящие перпендикулярно плоскости падения, создают луч 2, который также будет перпендикулярен падающему лучу, но будет лежать в плоскости падения. Этот луч будет полностью поляризован перпендикулярно плоскости падения (поле E₂). Таким образом, свет, рассеянный в направлениях, перпендикулярных первичному лучу, полностью поляризован. В других направлениях рассеянный свет будет частично поляризован.

При наблюдении под углом отличном от (в обе стороны) к направлению распространения падающего пучка к поляризованному вдоль какой-либо оси, например, вдоль оси X рассеянному свету неизменной интенсивности примешивается не когерентный с ним свет, поляризованный в плоскости XY, интенсивность которого изменяется как В результате степень поляризации рассеянного света постоянно уменьшается, обращаясь в нуль при и а его интенсивность изменяется как Поэтому при определении интенсивности рассеянного неполяризованного света в формуле (3.2) следует заменить на Этим объясняется появление указанного множителя в уравнении индикатрисы рассеяния естественного света (13.).