Глава 11

ПОЛЯРИЗАЦИЯ СВЕТА

11.1. Поляризованный и естественный свет

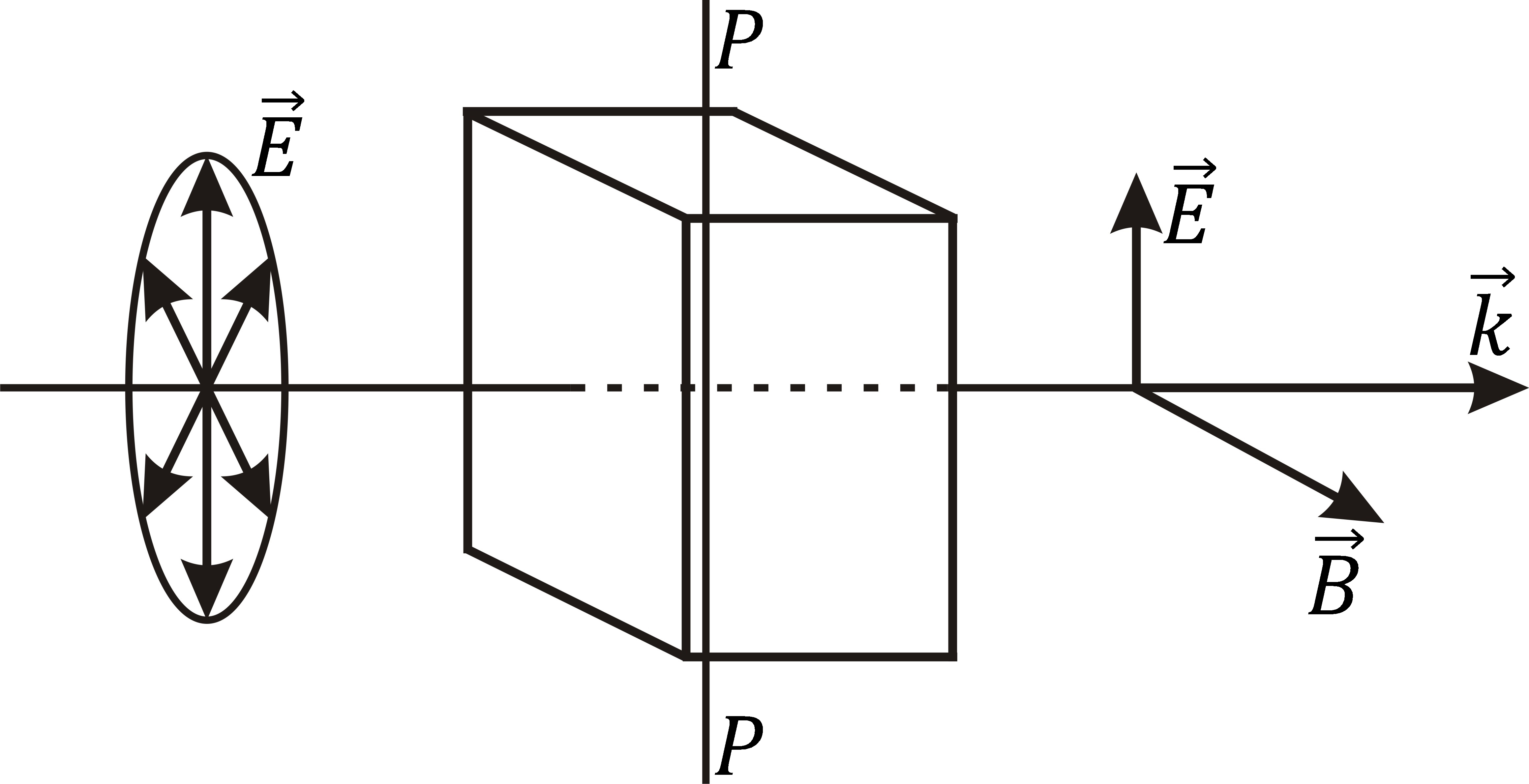
Свет, в котором направления колебаний электрического E (и связанного с ним магнитного B) вектора каким-либо образом упорядочены, называется поляризованным. Все возможные виды поляризации световой волны были рассмотрены в п. 1.2.4 и показаны на рис. 10.1. Наличие определенной поляризации не есть необходимое свойство световой волны.

а) б) в)

Рис. 11.1

Свет от реальных источников обычно не обнаруживает признаков поляризации. Световая волна, излучаемая одним атомом, обладает строго определенной поляризацией. Но если взять обычный (естественный) источник света, то он дает неполяризованный свет. Это связано с тем, что естественный источник содержит огромное число излучающих атомов. Излучаемые ими цуги волн имеют самые различные ориентации плоскостей поляризации. При наложении они дают свет, в котором вектор E в каждой точке непрерывно и беспорядочно (хаотически) меняет свою величину и направление в плоскости, перпендикулярной лучу. Такой свет называют естественным светом. Все направления в плоскости в среднем оказываются равноправными, поэтому естественный свет обладает (статистически) осевой симметрией относительно направления его распространения. Разлагая вектор E естественного, как и поляризованного, света на две взаимно перпендикулярные составляющие E_x и E_y, мы тем самым можем представить естественный свет как наложение двух плоско поляризованных волн с взаимно перпендикулярными плоскостями поляризации. Однако в отличие от поляризованной световой волны фазы этих волн и их амплитуды непрерывно и хаотически меняются во времени и никак не скоррелированы друг с другом. Это приводит к тому, что различные эллипсы поляризации беспорядочно сменяют друг друга, что, в конечном счете, и приводит к осевой симметрии волны.

Покажем, что амплитуда световой волны будет случайной величиной даже в том случае, если идентичные атомы излучают плоские монохроматические волны с одинаковой частотой w и волновым вектором k. Запишем поле излучения j-го атома в виде

E_j = E_{0 j} exp{– i [w (t – t_j) – k×r]},

где t_j – начало отсчета времени j-го атома (время начала излучения). Поле E_j будем считать эллиптически поляризованным. Результирующее поле E = E₀ exp[– i(w t – k×r)], создаваемое всеми атомами определится как сумма полей, создаваемых каждым атомом. С учетом этого будем иметь

E₀ =

Входящие в эту сумму величины t_j являются случайными, случайными являются также и углы между осями эллипсов поляризации. Поэтому случайной величиной является и амплитуда E₀.

Кроме поляризованного и естественного света возможен также свет частично поляризованный. В частично поляризованном свете колебаний электрического поля E (и магнитного поля B) одного направления преобладают над колебаниями других направлений, т.е. имеется предпочтительное, наиболее вероятное направление колебаний электрического поля E (и магнитного поля B). Такой свет можно рассматривать как смесь линейно поляризованного сета с естественным. Пучок частично поляризованного света можно считать суперпозицией двух пучков, один из которых является поляризованным, а другой – неполяризованным.

Выделение поляризованного света из естественного называют поляризацией света. Линейно поляризованный свет можно полу-

Рис. 11.2

чить из естественного с помощью специальных устрой- ств, называемых поляризаторами. Поляризаторы свободно пропускают свет с электрическим вектором E, параллельным некоторой плоскости, которую называют плоскостью поляризатора и задерживают (поглощают) свет с электрическим вектором, перпендикулярным этой плоскости. Пропустив через

Рис. 11.3

поляризатор естественный луч, мы получим линейно поляризованный свет с колебаниями электрического вектора E, совершающимися в плоскости поляризатора (рис. 10.2). Свет с круговой и эллиптической поляризацией получают наложением двух ортогонально поляризованных волн с определенной разностью фаз.

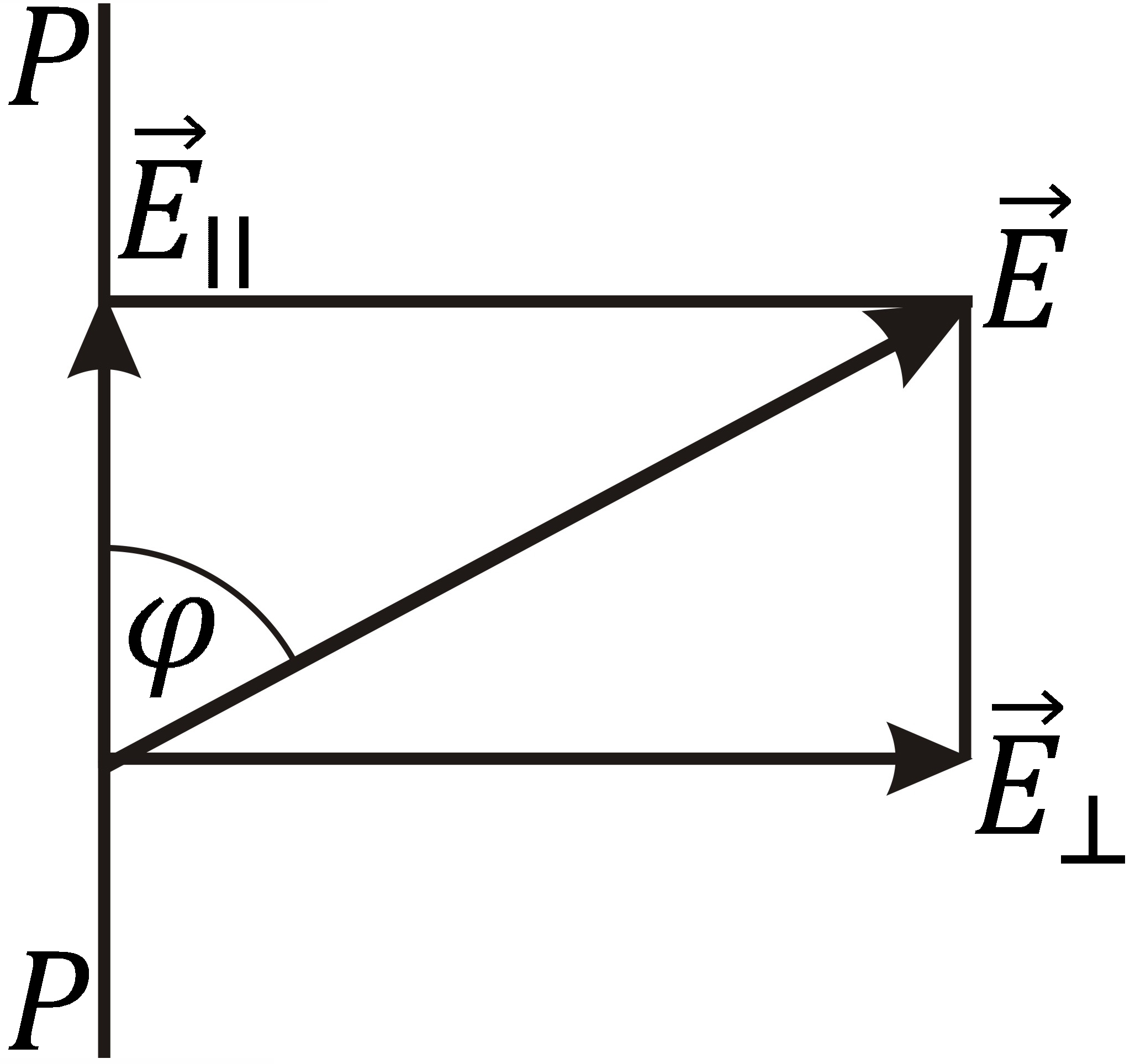
Найдем интенсивность прошедшей через поляризатор света. Представим естественный свет в виде двух плоско поляризованных волн: с вектором E, расположенном в плоскости поляризатора РР и с вектором E, перпендикулярным этой плоскости (рис. 10.3). Через поляризатор пройдет только составляющая E_|| = E cosj. Интенсивность прошедшего света

I =

Так как свет неполяризованный, то угол между вектором E и плоскостью РР поляризатора хаотически изменяется со временем, поэтому Тогда учитывая, что интенсивность естественного света, падающего на анализатор, I = получим для интенсивности прошедшего через поляризатор света Как видим, она в два раза меньше интенсивности, падающего на поляризатор света.

Чтобы убедиться, что полученный свет поляризован, и определить направление поляризации, поставим на пути луча, прошед-

Рис. 11.4

шего через поляризатор, второй такой же поляризатор, называемый в этом случае анализатором. Если плоскости пропускания поляризатора РР и анализатора АА параллельны друг другу, то плоско поляризованный свет пройдет через анализатор, не снижая своей интенсивности. Если же плоскости РР и АА перпендикулярны друг другу, то плоско поляризованный свет полностью задержится (поглотится) анализатором. В этом случае говорят, что поляризатор и анализатор скрещены. В промежуточных случаях интенсивность света, прошедшего через анализатор, будет зависеть от угла α между плоскостями РР и АА. Разложим луч, прошедший через поляризатор и, следовательно, поляризованный в плоскости РР, на два луча, один из которых поляризован в плоскости АА (E_||), а другой – в перпендикулярной ей плоскости (E_^, рис. 11.4). Через анализатор пройдет составляющая E_|| = E cosα, а E_^ поглотиться в нем. Так как a не зависит от времени, то интенсивность прошедшего через анализатор света

I =

откуда

(11.1)

где I = – интенсивность падающего на анализатор поляризованного света. Соотношение (15.1) называют законом Малюса. Вращая анализатор вокруг направления луча, мы будем наблюдать изменение интенсивности в пределах от значения до значения

Свет, прошедший через поляризатор, обычно оказывается не полностью, а частично поляризованным. Степень линейной поляризации света можно характеризовать величиной

(11.2)

У полностью поляризованного света степень поляризации , так как этом случае свет через анализатор не проходит, а значит, У естественного света , поскольку в нем волны разных направлений поляризации смешаны в равной степени и все направления эквивалентны, так что У частично поляризованного света 0 < , в этом случае свет частично проходит через анализатор, и