- •Глава 5
- •5.1. Интерференция световых монохроматических волн
- •5.2. Расчет интерференционнойткартины от двух
- •5.3. Методы получения когерентных световых пучков
- •5.4. Интерференция по методу деления волнового фронта. Опыт Юнга
- •5.5. Интерференция по методу деления амплитуды
- •5.5.1. Интерференция в тонких пленках
- •5.5.3. Интерферометр Майкельсона
- •5.6. Частичная когерентность. Корреляция
- •5.7. Времена́я и пространственная когерентность
- •5.8. Интерференция света и фотоны
5.7. Времена́я и пространственная когерентность
Контрастность и стационарность интерференционной картины зависит от разности хода волн . При = 0 контрастность и стационарность максимальные. С увеличением контрастность уменьшается и при некотором значении = l исчезает совсем. Это объясняется следующим образом. При = 0 обе части каждого цуга, испускаемого источником и раздвоенного в точке деления, приходят в точку встречи Р одновременно и полностью накладываются друг на друга. Интерференционная картина при этом имеет наивысшую контрастность. С увеличением разности хода часть цуга, идущая по более длинному пути, будет отставать от части цуга, идущей по более короткому пути, вследствие чего в точке Р будет происходить их частичное наложение. Это приведет к ухудшению контрастности полос. Если разность хода превысит длину цуга l, то часть цуга, идущая по короткому пути, минует точку встречи раньше, чем другая часть цуга достигнет ее. Произойдет наложение частей цугов, порожденных цугами, испущенными разными атомами либо одним и тем же атомом, но в разные моменты времени, а эти цуги не когерентны. Поэтому, когда разность хода станет не меньше длины цуга l, т.е. когда ∆ l, интерференционная картина не возникает – интерференция не наблюдается.
Способность световых волн к интерференции после разделения пучка света на два пучка и последующего их наложения с некоторой разностью хода называется временно̀й когерентностью, а максимальная разность хода ∆max, при которой интерференционная картина еще наблюдается, – длиной когерентности lког. Очевидно, что длина когерентности равна протяженности цуга l.
Длина цуга l связана с его длительностью , l = c, а значит, и с шириной его спектрального интервала (с учетом соотношения неопределенностей 2 / ) соотношением l = = c = 2 c / . Перейдя от круговой частоты к линейной частоте , это соотношение можно записать в виде l c / . Следовательно, длина когерентности
lког = c = c / .
Под шириной спектрального интервала следует понимать ширину спектрального интервала излучения источника квазимонохроматичекого света, так как спектральная ширина излучения реального квазимонохроматического источника определяется значением спектральной ширины отдельного цуга, испускаемого источником. Величину
tког = lког/c = 1 /
называют временем когерентности. Оно определяет ту максимальную временну́ю задержку одной части цуга по отношению к другому, при которой еще наблюдается интерференция.
На практике, однако, обычно имеют дело не со временем, а с длиной когерентности.
Длину когерентности удобно выразить через ширину интервала длин волн излучения источника . Так как
= (с / ) = (с / 2 )
(знак минус опущен, так как он только показывает, что с ростом длины волны частота убывает), то получим
lког
=
 ,
(2.43)
,
(2.43)
где – среднее значение длины волны из спектрального интервала . Длине когерентности соответствует максимальное число интерференционных полос
mmax = lког / = / .
Подставив в эту формулу lког = c tког = c, = cT0, где T0 =
= 2 / 0 – период колебания поля, получим
mmax = / T0.
Следовательно, максимальный порядок интерференции равен числу периодов колебаний, содержащихся в цуге излучения. При этом поскольку >> T0, то когерентность сохраняется на протяжении большого числа периодов колебаний поля.
Формула (2.43) показывает, что немонохроматичность световых волн приводит к ограничению разности их хода для наблюдения интерференции. Чем больше ширина спектрального интервала , тем меньше эта разность хода и тем, следовательно, труднее наблюдать интерференцию. С другой стороны, если бы световая волна была строго монохроматической ( = 0), то длина когерентности lког = , и интерференция наблюдалась бы при любой разности хода. Для обычных (не лазерных) источников света относительная ширина спектрального интервала / 10 - 3 – 10 – 5, так что длина когерентности имеет порядок 0,1 мм – 1 см. Для белого света средняя длина волны 0,55 мкм, а = 0,76 – – 0,38 = 0,38 мкм, поэтому длина когерентности lког 1 мкм, а mmax 1. Вот почему интерференцию белого света получить очень трудно. Для лазерного излучения относительная ширина спектрального интервала / может быть 10 – 11 и более, чему соответствует длина когерентности lког 10 5 и более. Поэтому интерференция света от лазерного источника наблюдается практически при любой разности хода. Более того, в экспериментах с лазерами для получения двухлучевой интерференции можно использовать не один источник, а два отдельных лазерных источника.
Мы видим, что временна̀я когерентность связана с немонохроматичностью света. Интерференция раздвоенного, а затем сведенного в одну точку пучка, возможна, если разность хода не будет превышать длину когерентности:
lког.
Это неравенство выражает собой, так называемое условие временно́й когерентности.
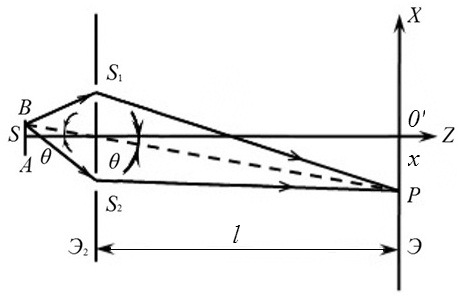
Рис. 5.
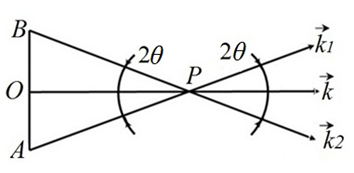
Наряду с временно́й когерентностью, существует и так называемая пространственная когерентность. Она связана с неточечностью источников света. Для ее рассмотрения обратимся снова к интерференционной схеме Юнга, заменив в ней точечный источник S на протяженный источник АВ (рис. 2.12). Возьмем какую-либо точку протяженного источника АВ. Свет, исходящий из этой точки, освещает отверстия S1 и S2 и на экране Э в окрестности точки O′ возникают интерференционные полосы. В зависимости от расстояния этой точки до оптической оси Z схемы существует определенная разность хода , величина которой и определяет положение максимумов и минимумов интенсивности полос на экране Э. Если бы источник состоял из одной только этой точки (как в идеализированном опыте Юнга), то наблюдались бы полосы с максимальной видностью. Однако реальный источник имеет конечный размер, и полосы, созданные излучением из других точек, будут смещены относительно полос, созданных излучением из S, и вследствие не когерентности этих элементарных излучений просто накладываются друг на друга. В результате такого наложения интерференционные полосы либо вовсе исчезают (если максимумы одной картины наложатся на минимумы другой), либо оказываются более или менее размытыми: видность интерференционных полос будет уменьшаться. Так как световые волны испускаются различными точками протяженного источника, то имеет место возникновение колебаний, возбуждаемых волнами с целым набором различных значений волнового вектора k. На рис. 6 показан источник света АВ, имеющий форму диска, видимый под углом 2θ из точки, расположенной посередине между отверстиями S1 и S2. Ввиду малости расстояния между отверстиями под тем же углом 2θ виден источник света и из самих отверстий S1 и S2. Из этого рисунка видно, что угол 2θ характеризует также интервал, в котором заключены векторы k. Будем считать этот угол малым.
Излучение источника будем предполагать монохроматическим, т.е. имеющим неограниченную длину когерентности. точечные
Рис. 5. |
отверстия S1 и S2 в плоском экране Э2 будем рассматривать в качестве произвольных точек S1 и S2 на псевдоволновой поверхности1. Будем рассматривать также случай, когда разность хода волн 0. Точка наблюдения Р в этом случае находится на одинаковом расстоянии от отверстий S1 и S2., т.е. на оптической оси интерференционной схемы. При этих предположениях результат интерференции в точке Р будет зависеть только от разности фаз колебаний в точках S1 и S2.
Центральный
(нулевой) максимум О′,
созданный излучением из крайней точки
В
источника смещен относительно центрального
максимума О,
создаваемого светом из центральной
точки S,
как видно из рис. 6 ввиду малости угла α
на ∆x
= lθ.
Если это смещение много меньше ширины
интерференционной полосы
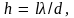 то максимумы от разных точек источника
практически наложаться друг на друга
и картина будет такой, как от точечного
источника. При
то максимумы от разных точек источника
практически наложаться друг на друга
и картина будет такой, как от точечного
источника. При
 максимумы от одних точек придутся на
минимумы от других, и интенрференционная
картина наблюдаться не будет. Таким
образом, интерференционная уартина
будет различимой при условии, что
максимумы от одних точек придутся на
минимумы от других, и интенрференционная
картина наблюдаться не будет. Таким
образом, интерференционная уартина
будет различимой при условии, что
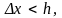 т.е.
т.е.
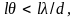 или
или
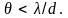 (6.)
(6.)
Формула (6.) определяет угловые размеры источника, при которых наблюдается интерференция. Из этой формулы можно определить также наибольшее расстояние d между отверстиями S1 и S2 (точками на псевдоволновой поверхности), при котором можно еще наблюдать интерференционную картину от источника с угловым размером 2θ:

Отсутствие
интерференционной картины означает,
что колебания возбуждаемые волной от
протяженного источника в местах
расположения отверстий S1
и S2
некогерентны.
Следовательно, и колебания в точах,
находящихся на псевдоволновой поверхности
на расстоянии d
друг от друга, являются некогерентными.
Способность к интерференции световых
волн, исходящих из двух пространственно
разделенных точек, взятых в поперечном
сечении светового пучка (на псевдоволновой
поверхности) называют пространственной
когерентностью, а масимальное расстояние
между указанными точками, при котором
колебания в них еще когерентны – радиусом
когерентности, обозначается ρког.
Принимают, что радиус когерентности
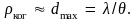
Угловой размер Солнца при наблюдении с Земли 10 – 2 рад, средняя длина волны солнечного света 0,5 мкм, следовательно, ког = / 0,05 мм. В п. 3.6 будет показано, что радиус когерентности круглого источника ког = 1,22 / , а поскольку Солнце при наблюдении с Земли представляется круглым светящимся диском, то более точное значение радиуса когерентности для солнечных лучей ког = 0,06 мм. Такое же расстояние d должно быть и между отверстиями S1 и S2 в схеме Юнга. Поэтому для уменьшения углового размера источника света и соответствующего увеличения d в опыте Юнга и ставится экран Э1 с узким отверстием. В лазерных источниках света, в отличие от обычных тепловых или газоразрядных источников, пространственная когерентность сохраняется поперек всего пучка. Причем его ширина для практических задач (например, при голографировании) может быть увеличена без потерь когерентности с помощью линз – расширителя пучка. Таким образом, свет лазера обладает не только временной, но и пространственной когерентностью. Очень похожим на свет лазера с точки зрения временной и пространственной когерентности являются радиоволны.
Следует обратить внимание на следующее обстоятельство. Рабочей характеристикой для определения возможностей получения интерференционной картины методом деления амплитуды является время или длина когерентности, зависящие от величины спектрального интервала излучения. В опытах, осуществляемых по методу деления волнового фронта, аналогичной величиной служит радиус когерентности, зависящий от угловых размеров источника излучения.