5.6. Частичная когерентность. Корреляция

В предыдущей главе речь шла об интерференционных явлениях, возникающих при наложении двух монохроматических волн, и способах получения когерентных световых пучков. Рассмотрим теперь возникновение интерференции в некоторой точке Р в случае, когда складываемые в ней волны от точечных источников S₁ и S₂ не являются строго монохроматическими. Будем считать, что источники S₁ и S₂ излучают квазимонохроматические волны с одинаковой центральной частотой  ₀:

E₁(t) = E₀₁(t)exp{-i[ ₀ t +  ₁(t)]},

E₂(t) = E₀₂(t)exp{-i[ ₀ t +  ₂(t)]}.

Учитывая что колебания светового поля, возбуждаемые источниками S₁ и S₂ в точке Р, запаздывают по сравнению с колебаниями самих источников, будем обозначать эти колебания как E₁(t - ₁) и E₂(t - ₂), где ₁ = r₁ / с и ₂ = r₂ / с - времена распространения первой и второй волн от источников S₁ и S₂ соответственно до точки наблюдения Р, r₁ и r₂ – расстояния от источников S₁ и S₂ до точки наблюдения Р. Введение времен ₁ и ₂ означает, что колебания в точке Р момент времени t такие же, как в точках S₁ и S₂ в моменты времени t - ₁ и t - ₂. Результирующее поле в точке Р, согласно принципу суперпозиции,

E(P) = E₁(t - ₁) + E₂(t - ₂),

а интенсивность в этой точке

I(P) = = + +

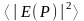+ 2Re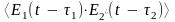 (2.32)

Смещение начального момента усреднения обычно не влияет на величину среднего (оптические поля, удовлетворяющие этому условию, называют стационарными), поэтому первые два слагаемых в (2.32) равны интенсивностям интерферирующих световых волн, так что

= = I.

Сместим начальный момент усреднения t в точку t = t – ₁, т.е. заменим t на t. Тогда, опустив штрих в символе t, третье слагаемое в (2.32) можно записать в виде 2Re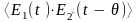 . Здесь  = ₂ – ₁ – относительное запаздывание колебаний E₂(t) и E₁(t) в точке наблюдения Р. Если разность хода волн от этих источников до точки наблюдения Р в равна  = r₂ – r₁, то колебания светового поля, создаваемые волной от одного источника (в нашем случае S₂), будут запаздывать по сравнению с колебаниями, создаваемыми волной от другого источника (S₁) на промежуток времени  =  / c. Среднее по времени наблюдения произведения комплексной амплитуды E₁(t) на комплексно сопряженную комплексной амплитуды E₂(t -  ), взятую в другой момент времени, отделенный от первого на промежуток , т.е. величину

Г₁₂( ) =

называют комплексной функцией корреляции колебаний E₁ и E₂ (создаваемых источниками S₁ и S₂ в точке Р). Ее также называют комплексной функцией временной когерентности колебаний или функцией взаимной когерентности. Она является количественной мерой коррелированности (согласованности) двух случайных процессов в два момента времени, разделенных промежутком . Следует отметить, что если сам волновой процесс E(t) является случайной функцией времени, то функция когерентности Г₁₂( ) детерминирована. Она определяет закон изменения (потери) статистической памяти с ростом . Функцию взаимной когерентности широко используют при анализе интерференционных явлений. Выразив усреднение через интегрирование, для этой функции можно записать

Г₁₂( ) = ,

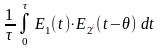где  - ширина временного интервала, по которому производится усреднение.

Функцию Г₁₂( ) нормируют, полагая

₁₂( ) = (2.33)

или

₁₂(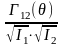 ) = . (2.34)

Нормированную функцию ₁₂() называют комплексной степенью взаимной когерентности (или корреляции колебаний), а ее модуль ₁₂( ) - степенью взаимной когерентности колебаний (в точке Р). Комплексная корреляционная функция Г₁₂( ), а следовательно, и степень взаимной когерентности ₁₂() отражают статистические свойства излучения. Заметим, что модуль числителя в (2.33) не превышает знаменателя, поэтому степень взаимной когерентности ₁₂( )  1. При  = 0 степень взаимной когерентности имеет максимальное значение, равное единице. С увеличением времени задержки  степень взаимной когерентности убывает и при каком-то значении   t_ког она обращается в нуль. Максимальное значение времени задержки

 = t_ког, при котором когерентность еще сохраняется, называется временем когерентности. Расстояние l_ког = ct_ког, проходимое светом за время когерентности, называется длиной когерентности. Таким образом, степень взаимной когерентности имеет значение, заключенное в интервале 0  ₁₂( )  1.

Величина ₁₂( ) доступна экспериментальному определению. Зная ее, можно проводить количественное изучение когерентных свойств оптических полей, определить возможность наблюдения интерференции в том или ином конкретном опыте.

С учетом выражения (2.1) и соотношения (2.34) для интенсивности в точке Р будем иметь

I(P) = I₁(P) + I₂(P) + 2 Re ₁₂( ). (2.35)

Эта формула может быть использована для определения

Re ₁₂( ). Для этого в опыте Юнга достаточно измерить в некоторой точке Р интерферограммы значение полной интенсивности I(P) и интенсивностей I₁(P) и I₂(P) света в этой же точке соответственно от каждого источника (отверстий S₁ и S₂) при закрытом другом источнике (отверстии).

При равных интенсивностях I₁(P) = I₂(P) = I₀(P) формула (2.35) упрощается:

I(P) = 2 I₀(P) [1 + Re ₁₂( )]. (2.36)

Представим комплексную функцию ₁₂( ) в виде

₁₂( ) = ₁₂( ) exp[- i ₁₂(  )],

где  ₁₂(  ) – аргумент комплексной функции ₁₂( ). Величину  ₁₂( ) можно рассматривать как обобщенную разность фаз между колебаниями световых полей в точке Р. Представим ее в виде суммы  ₁₂(  ) =  +  ( ), где  - разность фаз, обусловленная разностью хода , а  ( ) – дополнительная разность фаз, зависящая от времени задержки  и обусловленная не строгой когерентностью волн (при этом  (0) = 0). Записав реальную часть в (2.35) как ₁₂( ) cos [ +  ( )], выражение (2.35) приведем к виду

I(P) = I₁(P) + I₂(P) + 2 ₁₂( ) cos [ +  ( )].

(2.37)

При равных интенсивностях обеих волн формула (2.37) принимает вид

I(P) = 2I₀ [1 + ₁₂( ) cos [ +  ( )].

Формула (2.37) известна как общий закон интерференции стационарных оптических полей. Она представляет собой наиболее общее выражение, определяющее результат интерференции двух квазимонохроматических волн и справедлива для любой двухлучевой интерференционной схемы. От формулы (2.1) для строго монохроматических световых волн формула (2.37) отличается дополнительным множителем ₁₂( ) в интерференционном члене и добавочным слагаемым  ( ) в разности фаз. Добавочное слагаемое  ( ) определяет фазовый сдвиг интерференционного максимума (или минимума) по сравнению с его положением в интерференционной картине при интерференции строго монохроматических волн. Фаза  ( ) измеряет сдвиг полос вдоль оси X в плоскости наблюдения. Если величина ₁₂() равна своему максимальному значению, единице, а величина  ( ) = 0, то интенсивность в точке Р будет такой же, как в случае монохроматического света с разностью фаз  = = (2 / ₀) между волнами. При таких условиях волны, излучаемые источниками S₁ и S₂, являются полностью когерентными. Если же величина ₁₂( ) равна другому своему предельному значению, нулю, то интерференционный член в (2.37) будет отсутствовать; интерференция не происходит, волны, излучаемые источниками S₁ и S₂, полностью не когерентны, а наблюдаемая интенсивность является простой суммой независимых интенсивностей, создаваемых источниками S₁ и S₂. Когда ₁₂( ) принимает свое промежуточное значение 0 < ₁₂( ) < 1, говорят о частичной когерентности световых волн. В соответствии с этим формулу (2.37) называют также общим законом интерференции для частично когерентного света. На практике световые волны считают близкими к полной когерентности, если 0,88  ₁₂( )   1 и частично когерентными, если 0  ₁₂( ) < 0,88. Интерференционные полосы наблюдаются достаточно четко и при видности V ≥ 2 / 3. В этом случае I_max ≥ 5I_min.

Частично когерентный свет можно рассматривать как смесь когерентного и некогерентного света. Величину ₁₂( ) можно трактовать как долю когерентного света, присутствующего в излучении. В этом случае интенсивность каждого интерферирующего пучка, например, первого, можно представить состоящим из двух слагаемых, I₁ = I₁ + (1 - )I₁, первое из которых (I₁) определяет интенсивность когерентного света, а второе ((1 - )I₁) - интенсивность некогерентного света.

Степень взаимной когерентности ₁₂( ) имеет те же пределы изменения (0  ₁₂( )  1), что и функция видности V(), определяемая соотношением (2.2). Покажем, что величины V() и ₁₂( ) связаны друг с другом. Действительно, ввиду медленности изменения функции ₁₂( ) максимальное и минимальное значения интенсивности получаются из соотношения (2.37) при cos [ +  ( )] =  1 соответственно. С учетом этого для видности интерференционных полос получим

V() = 2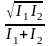 ₁₂( ). (2.38)

Это и есть формула, выражающая связь видности полос V() со степенью взаимной когерентности ₁₂( ). С помощью этой формулы можно экспериментально определить степень взаимной когерентности ₁₂( ) исследуемого излучения по измерениям видности V() интерференционных полос при различных значениях разности хода  = c. По расположению полос можно судить об аргументе комплексной функции ₁₂(). Действительно, согласно (2.37) максимум порядка m наблюдается при условии  +  ( ) = 2m, где 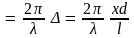 , d и l – параметры схемы Юнга, x – расстояние от центра интерференционной картины до m-го максимума. Измеряя эти расстояния, находим

 ( ) .

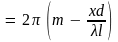Подобные измерения, однако, выполнить довольно сложно.

При одинаковых значениях интенсивностей интерферирующих волн (I₁ = I₂) функция видности V() и степень взаимной когерентности 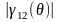будут равны друг другу, V() = , при всех значениях  = c. В этом случае при = 0 будет и V() = 0, т.е. в случае полностью некогерентных световых волн интерференционные полосы не наблюдаются. Если же = = 1, то и V() = 1. В этом случае имеет место полная когерентность световых волн с резко выраженной интерференционной картиной. Интерференционная картина получается такой, какой она имеет место в модели монохроматических волн. Случай 0 < V() < 1 соответствует, очевидно, частичной когерентности. При I₁  I₂ функции V() и так же одновременно достигают своего максимального и минимального значения, но эти значения для функции V() не равны соответствующим значениям для функции .

Из формулы (2.38) видно, что видность интерференционной картины V() при любой разности хода  зависит также от соотношения интенсивностей I₁ и I₂. Положив в этой формуле = 1, и введя отношение интенсивностей p = I₁ / I₂, получим

V() = 2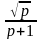 . (2.39)

Из расчета по этой формуле величины V() следует, что при p = = 1 (равных интенсивностях) V() = 1, при p = 2 V() = 0,94, при p = 3 V() = 0,87 и т.д. Как видим, даже при трехкратном различии интенсивностей величина V близка к единице, когда ₁₂ в точности равна единице. Поэтому неравенство интенсивностей интерферирующих волн не оказывает решающего влияния на контраст интерференционной картины.

Сравнивая формулу (2.1), определяющую видность интерференционных полос при полной когерентности, с формулой (2.38), видим, что степень взаимной когерентности колебаний показывает, во сколько раз контраст интерференционной картины при частичной когерентности меньше контраста при полной когерентности. Следовательно, функцию можно трактовать и как меру уменьшения контраста при интерференции немонохроматических волн.