5.5. Интерференция по методу деления амплитуды

5.5.1. Интерференция в тонких пленках

В качестве примера интерференции света по методу деления амплитуды рассмотрим интерференцию, возникающую при отражении и преломлении светового пучка на границах прозрачной плоскопараллельной пластинки. Падающий на пленку под углом a (рис. 3.7, а) пучок 1 монохроматического света частично отражается от верхней поверхности пленки (луч 1¢) и частично преломляется (луч 2). После отражения луча 2 от нижней поверхности пленки возникает луч 2¢, который, преломляясь затем на верхней поверхности, переходит в луч 1¢¢. При таком частичном отражении и преломлении и происходит деление падающей световой волны по амплитуде. Интерференция происходит между лучами 1¢ и 1¢¢. Если пленка достаточно тонкая, то оптическая разность хода лучей 1¢ и 1¢¢ будет не слишком большой (меньше длины когерентности). Поэтому лучи эти будут когерентными, а их интенсивности - не слишком отличаться друг от друга (малое различие интенсивностей необходимо для увеличения контрастности интерференционной картины, так как V тем больше, чем ближе I₁ и I₂ друг к другу). Результат интерференции лучей будет определяться разностью хода между ними. (Как видим и здесь имеет место двухлучевая интерференция.)

Разность хода лучей 1¢ и 1¢¢ возникает лишь при их распространении до плоскости CD. Оптический путь луча 1¢ до этой плоскости равен AD, а луча 1¢¢ - соответственно n(AB + BC ), где n – показатель преломления материала пленки. Оптическая разность хода этих лучей составит

D = n(AB + BC ) – (AD + l₀ / 2),

где добавочное слагаемое l₀ / 2 во вторых скобках учитывает потерю полволны (изменение фазы на p) при отражении волны от оптически более плотной среды (предполагается, что пленка находится в воздухе с показателем преломления n₁ = 1).

Так как пленка плоскопараллельная, то AB = BC = d / cosa AD = AC sina = 2d tga ₂ × sina. Используя закон преломления sina / sina ₂ = n, после несложных преобразований для оптической разности хода интерферирующих лучей получим

D = 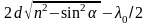. (2.10)

При нормальном падении света на пленку (a = 0) оптическая разность хода интерферирующих лучей 1¢ и 1¢¢ будет

D = 2dn - l₀ / 2.

Рис. 5.

Результат интерференции в отраженном от пленки свете, как видно из (2.10), зависит от численных значений d, a и l₀. При оптической разности хода D = ml₀ наблюдается максимум отражения, а при D = (m + 1 / 2)l₀ – минимум отражения, где m – порядок интерференционного максимума или минимума.

Если на поверхность пленки падает непараллельный пучок света (угол наклона a различен для разных лучей), то будут наблюдаться интерференционные полосы, отвечающие одинаковым углам a. Эти полосы называют полосами равного наклона. Если же толщина d пленки в разных местах разная (напрмер, в случае пленки в виде клина), то будут наблюдаться полосы, отвечающие участкам одинаковой толщины. Лучи 1¢ и 1¢¢ при этом имеют различные нправления и пересекаются только в точках верхней поверхности пленки. Поэтому эти полосы, называемые полосами равной толщины, локализованы на поверхности пленки. Полосы равного наклона локализованы в бесконечности, так как лучи 1¢ и 1¢¢ в этом случае параллельны.

При освещении плоскопараллельной пленки белым светом условие максимума будет выполняться лишь для одной определенной длины волны и вся поверхность пленки окрасится в один определенный цвет, причем с изменением угла наклона эта окраска будет меняться. Для пленки переменной толщины эта окраска будет на разных участках различна.

Интерференцию можно наблюдать не только в отраженном, но и в проходящем свете ( в свете, прошедшем через пленку). В этом случае интерферируют лучи 3¢ и 3¢¢ (рис. 2.2). Луч 3¢ выходит прямо из пленки (приломившись под углом a на нижней поверхности), а луч 3¢¢ - после двух отражений внутри пленки. При малой толщине пленки эти лучи будут когерентными. Потери полволны при этом не происходит, так как лучи, от которых образуется луч 3¢¢, отражаются от оптически менее плотной среды. Оптическая разность хода этих лучей D = n(BC + CF ) – BE. Действуя так же, как и в предыдущем случае, будем иметь D = = . Легко видеть, что при такой разности хода там, где в отраженном свете наблюдаются максимумы интерференционной картины, в проходящем свете наблюдаются минимумы, и наоборот. В этом смысле интерференционная картина в проходящем свете является дополняющей к интерференционной картине в отраженном свете.

5.5.2. Кольца Ньютона

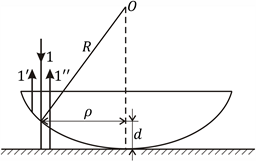
Интерференционные полосы равной толщины можно наблюдать при падении света на плосковыпуклую линзу малой кривизны, соприкасающуюся в воздухе с плоской поверхностью стекла (рис. 2.2, б). Падающий нормально на плоскую поверхность линзы и прошедший сквозь ее толщу пучок 1 монохроматического света, частично отражается от границы раздела линза – воздух (луч 1¢), частично проходит в воздух (преломляется) и затем отражается от границы раздела воздух – стекло (луч 1¢¢).. Интерференция происходит между двумя вторичными лучами 1¢ и 1¢¢.

Заметим, что, кроме лучей 1¢ и 1¢¢, возникают еще лучи, отраженные от верхней и нижней поверхностей линзы. Однако эти лучи не интерферируют, так как из-за бльшой их оптичкской раз-

Рис. 6.

ности хода, обусловленной большой толщиной линзы, они оказываются некогерентными.

Разность хода лучей 1¢ и 1¢¢ равна 2d, где d – толщина воздушного слоя в месте падения луча, зависящая от расстояния ρ до точки касания линзы со стеклом и радиуса кривизны линзы R. С помощью рис. 2.2, б и условия ρ << R, т.е. при (ρ / R) ² << 1, находим толщину воздушного промежутка:

@ ρ ² / 2R.

Разность фаз рассматриваеых лучей в отраженном свете равна

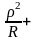d = (2p / l₀) 2d + p p,

где добавочное слагаемое p учитывает изменение фазы на p при отражении от стеклянной пластинки как от оптически более плотной среды, чем воздух. При освещении установки монохроматическим пучком света в отраженном свете будет наблюдаться интерференционная картина в виде чередующихся светлых и темных колец. Эти кольца называют кольцами Ньютона.

Условием образования светлых интерференционных колец является соотношение

,

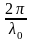
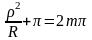где m – целое положительное число за исключением нуля. С учетом этого находим радиусы светлых колец Ньютона:

ρ_m = . (2.11)

Темные кольца, возникающие при выполнении условия

,

имеют радиусы

ρ_m = 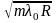, (2.12)

где m – целое положительное число, включая нуль.

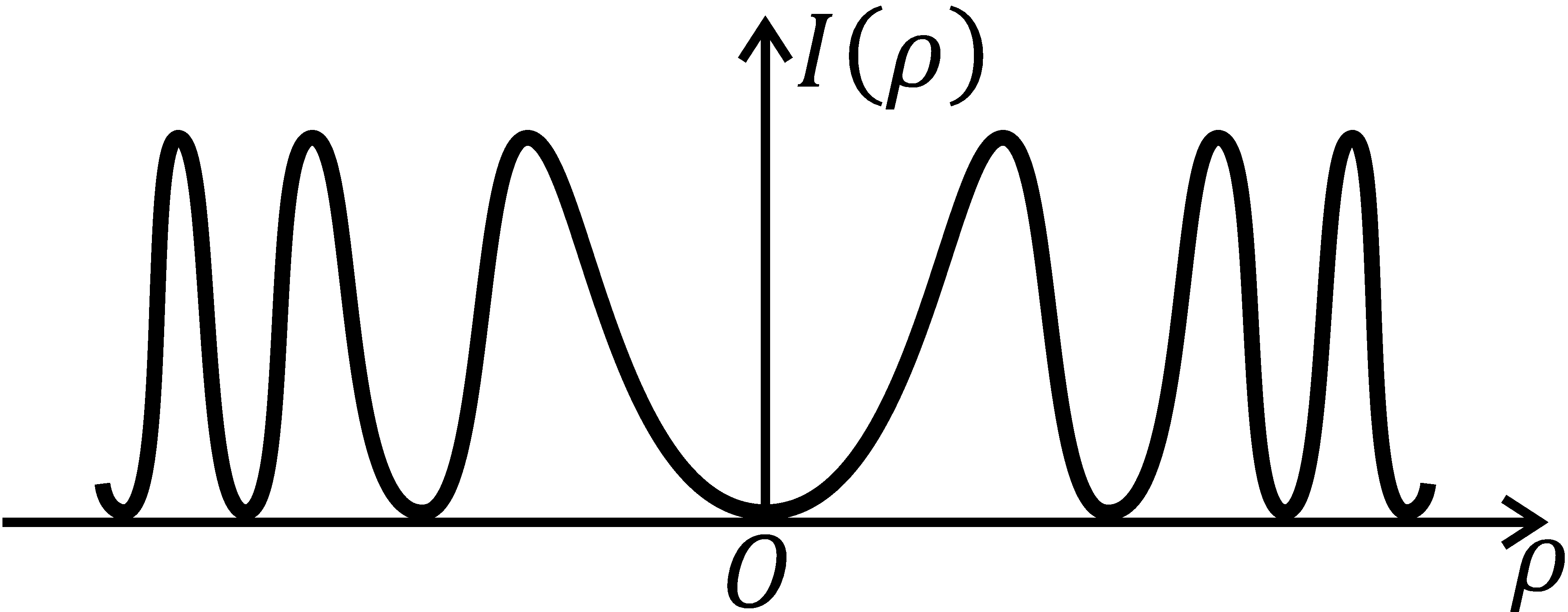
Рис 6.

С помощью формулы (2.11) или (2.12) можно определить длину волны используемого света. Для этого следует измерить ради

ус m- го светлого или темного интерференционного кольца и радиус кривизны R линзы.

Таким образом, радиусы светлых колец Ньютона пропорциональны квадратному корню из полуцелых чисел, а темных – квадратному корню из натуральных чисел. Центр интерференционной картины (в отраженном свете) будет темным, так как в окрестности точки соприкосновения линзы с пластинкой толщина воздушной прослойки d @ 0, а разность фаз d интерферирующих лучей примерно равна p. Центру интерференционной картины соответствует радиус кольца r_m = 0, что имеет место при m = 0.

Интерференционная картина в проходящем свете будет дополняющей к интерференционной картине в отраженном свете. Радиусы темных колец будут определяться формулой (2.11), а светлых – формулой (2.12).