5.4. Интерференция по методу деления волнового фронта. Опыт Юнга

Простейшей двухлучевой интерференционной схемой, в которой используется метод деления волнового фронта, является схема Юнга, показанная на рис. 3.6.

Пучок света падает на экран Э₁ с узким отверстием S или щелью. Прошедший через отверстие S свет, вследствие дифракции образует расходящийся пучок, который падает на второй экран Э₂

Рис. 6.3

с двумя узкими отверстиями или щелями S₁ и S₂, расположенными близко друг к другу и на равных расстояниях от S. Когда фронт волны из S достигнет этих отверстий, они, согласно принципу Гюйгенса, становятся источниками вторичных волн. Эти вторичные источники являются когерентными, так как колебания в них возбуждаются одной и той же падающей на экран волной. Испускаемые ими расходящиеся волны накладываются друг на друга и создают интерференционную картину, наблюдаемую на экране Э, находящемся на достаточно большом удалении от экрана Э₂. Так как источники S₁ и S₂ колеблются в одинаковых фазах, начальная разность фаз испускаемых ими волн равна нулю. Поэтому разность фаз этих волн в точке их наложения Р будет d = (2p / l₀)D, где D = nD₀ = n(r₂ – r₁) – оптическая разность хода, а D₀ = r₂ – r₁ – геометрическая разность хода волн, испускаеых источниками S₁ и S₂; n – показатель преломления среды, заключенной между экранами Э₂ и Э; r₁ и r₂ – расстояние от источника S₁ и S₂ до точки наблюдения P.

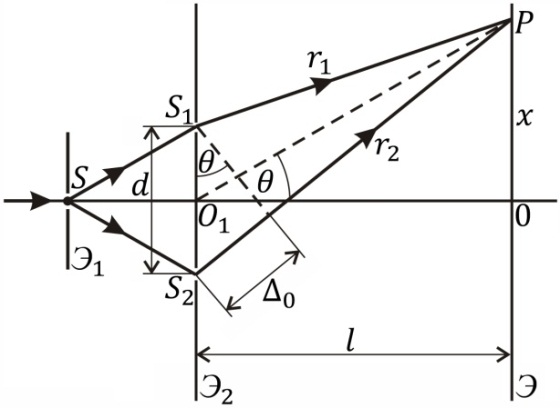
Пусть q – угол, образуемый направлением на точку Р с оптической осью O₁O схемы, т.е. с линией, перпендикулярной экранам

Э₂ и Э и проходящей через середину расстояния между щелями S₁ и S₂. Этот угол мал (q << 1), так как расстояние d между источниками S₁ и S₂ много больше расстояния l от этих источников до экрана Э (l >> d), поэтому, как видно из рис. 2.1, D₀ @ d×q . Но q @ @ x / l, где x – расстояние от точки Р на экране Э до плоскости, перпендикулярной S₁S₂ и содержащей оптическую ось O₁O, т.е. вертикальная координата точки Р. Следовательно,

D₀ @ x d / l. (2.)

Так как отверстия S₁ и S₂ одинаковы, а r₁ @ r₂ (поскольку D₀ << << l ), то интенсивности I₁(P) и I₂(P), создаваемые источниками S₁ и S₂ в точке P, можно считать одинаковыми, поэтому результирующую интенсивность I(P) в точке P млжно расчитать по формуле (3.21). Зависимость интенсивности от координаты x в плоскости наблюдения показана на рис. 6.

Расчет разности хода лучей в других интерференционных схемах по методу деления волнового фронта, ничем не отличается от рассмотренного выше для схемы Юнга (эти схемы фактически эквивалентны схеме Юнга). Во всех таких схемах ход лучей, пересекающихся в точке Р, таков, что как будто эти лучи исходят не из реального источника S, а из двух когерентных источников (действительных или мнимых) S₁ и S₂, расположенных на расстоянии d друг от друга и на расстоянии l от экрана, на котором наблюдается интерференционная картина. Задача заключается лишь в том, чтобы выразить расстояния d и l через параметры схемы.