Глава 5

ИНТЕРФЕРЕНЦИЯ СВЕТА

5.1. Интерференция световых монохроматических волн

Пусть в некоторой точке пространства Р происходит наложение двух монохроматических световых волн, частоты которых соответственно равны w ₁ и w ₂. Будем предполагать, что создаваемые этими волнами колебания электрических векторов E₁ и E₂ происходят в одном направлении. В этом случае векторный характер полей E₁ и E₂ можно не учитывать, и считать, что

E₁(t) = E₀₁ exp [– i (w ₁ t + j ₁)],

E₂(t) = E₀₂ exp [– i (w ₂ t + j ₂)],

где фаза j _i = – k _i × r + α_i – для плоских волн и j _i = – k _i r_i + α_i – для сферических волн, r – радиус-вектор, определяющий положение в пространстве точки наблюдения Р, r_i – расстояние, проходимое i-ой волной до точки наложения волн P, i = 1, 2. В соответствии с принципом суперпозиции электрических полей, для результирующей напряженности поля в точке Р будем иметь

E(P) = E₁(P) + E₂(P).

Принцип суперпозиции является следствием линейности уравнений Максвелла и вытекающих из них общего волнового уравнения и уравнения Гельмгольца: если поля E₁(r, t) и E₂(r, t) являются решением волнового уравнения, то его решением является и линейная комбинация этих полей, в частности, их сумма.

Так как частота света составляет примерно 10¹⁴ Гц, то используемые на практике детекторы светового излучения, например, фотопленка, фотопластинка, фотодиоды, а также сетчатка глаза, вследствие своей инерционности, не в состоянии реагировать на столь быстрые изменения светового поля. Обычно они не позволяют следить и за быстрыми изменениями световых потоков, обусловленных случайными изменениями амплитуд и фаз колебаний. Поэтому все детекторы светового излучения могут измерять только величины, пропорциональные квадрату напряженности световых полей; они реагируют на интенсивность, которая представляет собой усредненную по времени плотность потока световой энергии и которая пропорциональна среднему по времени наблюдения квадрату модуля (в комплексном представлении поля) напряженности электрического поля. Имея в виду определение интенсивности света, найдем величину 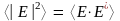. Получим

=

= .

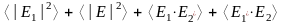Здесь четвертый член является комплексно сопряженным третьему члену. Сумма таких слагаемых равна удвоенному значению реальной части одного из них:

= .

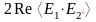Преобразуем это слагаемое:

=

= 2 | E₀₁ |×| E₀₂ |× =

= 2 | E₀₁ |×| E₀₂ | ,

где d = (w ₁ – w ₂) t + j ₁ – j ₂ – разность фаз складываемых в точке Р волн. Следовательно,

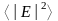= + + 2 | E₀₁ |×| E₀₂ | .

К такому же выражению можно прийти также, используя формулу

exp(ia) + exp(- ia) = 2 cosa.

Учитывая, что |E₀₁| ² = I₁ |E₀₂| ² = I₂, |E₀₁|×|E₀₂| =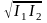 , для интенсивности света в точке Р получим

I(P) = I₁(P) + I₂(P) + I₁₂(P),

где

I₁₂(P) = 2 .

Слагаемое I₁₂(P) называют интерференционным членом. Им определяются все интерференционные эффекты, связанные с характером изменения интенсивности в пространстве.

Если w ₁ ¹ w ₂, то разность фаз складываемых волн d будет зависеть от времени: d = d (t). Среднее значение косинуса, а с ним и интерференционный член I₁₂(P), обратятся в нуль и тогда

I(P) = I₁(P) + I₂(P),

т.е. имеет место суммирование интенсивностей. Если же w ₁ = w ₂ и разность начальных фаз j ₁ - j ₂ не зависит от времени (для монохроматических волн второе условие всегда имеет место), то 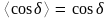тождественно не равен нулю. Тождественно не равным нулю будет и интерференционный член I₁₂(P). В этом случае

I(P) = I₁(P) + I₂(P) + 2 cosd , (6.1)

где разность фаз d = j ₁ – j ₂ не зависит от времени. В зависимости от величины разности фаз d, которое определяется положением точки набдюдения Р, множитель cosd в интерференционном члене I₁₂(P) может принимать как положительные, так и отрицательные значения. Поэтому результирующая интенсивность I(P) в точке Р будет либо больше, либо меньше суммы интенсивностей складываемых волн. В одних точках волны при наложении будут усиливать друг друга, а в других – ослаблять. В точках, для которых cosd = +1, разность фаз d = 2mp, где m – целое число, включая нуль, интенсивность будет достигать максимального значения , а для которых cosd = –1, разность фаз d = (2m + 1)p, – минимального значения . 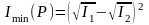При этом при равных интенсивностях (I₁ = I₂ = I₀) I_max = 4I₀, а I_min = 0.

Таким образом, при сложении двух монохроматических световых волн результирующая интенсивность в каждой точке пространства Р равна сумме интенсивностей складываемых волн, если их частоты различны, и отличается от суммы интенсивностей, если частоты волн одинаковы. Во втором случае в зависимости от конкретного значения разности фаз d = j ₁ – j ₂, которое определяется положением точки наблюдения Р, интенсивность I(P) может принимать различные, не равные сумме интенсивностей, значения. Имеет место перераспределение интенсивности света в пространстве так, что в одних точках пространства световые волны усиливают друг друга, а в других ослабляют. Это явление устойчивого во времени перераспределения колебаний светового поля в пространстве, в результате которого в одних местах колебания усиливаются, а в других ослабляются, называется интерференцией света. Область перекрытия волн называется интерференционным полем. В точках, где волны усиливают друг друга, образуются максимумы интенсивности света, а где ослабляют – минимумы интенсивности. Их называют соответственно интерференционными максимумами и интерференционными минимумами. Интенсивность всех интерференционных максимумов одинакова. На экране, расположенном подходящим образом в области наложения волн (в волновом поле), этим максимумам и минимумам будут соответствовать светлые и темные полосы, называемые интерференционными полосами. Расстояние h между соседними максимумами или минимумами интенсивности (светлыми или темными полосами) называется шириной интерференционной полосы. Таким образом, h = x_m –– x_{m - 1}, где x_i (i = m, m – 1) – координата i-го максимума или минимума. Устойчивую во времени картину чередования темных и светлых полос называют интерференционной картиной. Конкретный вид и форма интерференционных полос, а значит, и вид интерференционной картины зависят от интерферирующих волн, т.е. от комплексных амплитуд E₁(r) и E₂(r), или, иначе, – от пространственного распределения амплитуд и фаз интерферирующих волн.

Соотношение (3.1) в теории двухлучевой интерференции монохроматических волн является основным. Из него следует, что интерференционный эффект определяется зависимостью разности фаз d от положения точки наблюдения. Чередование темных и светлых полос, характерное для интерференции света, связано с изменением знака cosd .

Световые волны, способные к интерференции, называются когерентными, в противном случае – некогерентными При наложении когерентных волн в точке Р устанавливаются гармонические колебания с постоянной амплитудой, различной в разных точках, а при наложении некогерентных – негармонические колебания с нерегулярно изменяющимися во времени амплитудами. Из сказанного ясно, что световые волны являются когерентными, если их разность фаз d не зависит от времени. Для монохроматических волн это имеет место, если их частоты одинаковы.

Полученные выше соотношения для двух источников можно обобщить на случай многих источников. Пусть свет в некоторую точку пространства приходит от большого числа источников. Тогда если источники света являются когерентными, то результирующая интенсивность в указанной точке

I_ког = ,

а если некогерентными –

I_неког = .

В результате можно сформулировать следующее утверждение: при когерентных источниках суммируются амплитуды полей и модуль суммы возводится в квадрат; при некогерентных источниках суммируются квадраты модулей, т.е. интенсивности полей. Следует при этом отметить, что переход от комплексной амплитуды к интенсивности, регистрируемой прибором, происходит только в детекторе излучения.