3.2. Ймовірнісні емм

3.2.1 Методи теорії ймовірностей та економетрії Ці методи застосовуються, коли зміну показників, що аналізують, можна подати як випадковий процес. Статистичні методи є основним засобом вивчення масових явищ, що повторюються та відіграють важливу роль у прогнозуванні поведінки економічних показників. Коли зв'язок між характеристиками, які аналізуються, не детермінований, а стохастичний, то статистичні та ймовірнісні методи - це практично єдиний інструмент дослідження. Найпоширеніші з математично-статистичних методів у фінансово-економічному аналізі методи множинного та парно-кореляційного аналізу. За допомогою цих методів встановлюється форма зв'язку (тип аналітичної залежності) між залежною і неза­лежною змінними. Наприклад, у загальному вигляді парна лінійна регресійна модель записується таким чином:

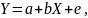
де У - вектор спостережень за залежною змінною; X - вектор спостережень за незалежною змінною; а,b - невідомі параметри моделі; е -вектор випадкових величин (помилок). Для визначення параметрів моделі найчастіше застосовується метод найменших квадратів (МНК).

Узагальнена багатофакторна лінійна регресійна модель може бути записана у такому вигляді:

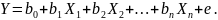
Методи теорії ймовірностей допомагають приймати рішення, що зводяться до знаходження значень ймовірностей настання певних подій, математичного сподівання тієї чи іншої випадкової величини і т.д. Зокрема, може йтися про наступне: ефективність рекламної кампанії; виробляти чи ні той чи інший товар; розширювати чи реорганізовувати виробництво; виходити на ринок чи ні тощо.

Приклади з теорії ймовірностей та економетрії (прогнозування купівельної спроможності)

3.2.2 Імітаційне моделювання - один із найсучасніших способів дослідження й прогнозування складних систем. Імітаційне моделювання можна визначити як процес конструювання математичної моделі реальної системи з наступним дослідженням і проведенням експериментів на цій моделі. Внаслідок вивчення поведінки моделі у різних умовах і за різних значень параметрів з'являється можливість прогнозувати поведінку реальної системи, передбачати наслідки тих чи інших управлінських дій або змін.

3.2.3 Методи теорії масового обслуговування. У багатьох галузях економіки, фінансів, виробництва й побуту важливу роль відіграють системи спеціального виду, що реалізують багаторазове виконання досить однотипних задач. Такі системи, призначені для обслуговування масового потоку вимог випадкового характеру, називають системами масового обслуговування (СМО). Прикладами СМО у фінансово-економічній сфері можуть бути системи, що представляють банки різних типів (комерційні, інвестиційні, іпотечні, ощадні), страхові орга­нізації (державні, комерційні товариства, компанії, асоціації тощо), податкові інспекції, різні системи зв'язку (у тому числі телефонні станції), завантажувально-розвантажувальні комплекси (порти, товарні станції), автозаправні станції, різні підприємства сфери обслуговування (магазини, довідкові бюро, перукарні, білетні каси і т.д.). Ці системи застосовуються для розв'язування задач про вибір черговості обслуго­вування замовників, при складанні графіків поставок товарів та в інших аналогічних випадках. Випадковими можуть бути як моменти появи вимог, так і витрати часу на їх обслуговування. Метою цих методів є відшуковування розумної організації обслуговування, що забезпечить задану якість, визначення оптимальних (з точки зору прийнятого критерію) норм чергового обслуговування, необхідність якого виникає непланомірно.

Приклад з теорії масового обслуговування.

3.2.4 Методи аналізу та управління ризиком в економіці У багатьох ситуаціях рішення треба приймати в результаті аналізу послідовності можливих рішень у ринковій обстановці, коли одна сукупність рішень особи, що їх приймає, і станів ринку породжує інший стан аналогічного типу. В момент такого переходу треба прийняти рішення з оцінкою можливих наслідків. Якщо число послідовних множин рішень більше одного, коли наступні рішення приймаються за результатами попередніх, використовують «дерево» розв'язків.

Приклад методу аналізу та управління ризиком в економіці

3.2.5 Метод статистичного моделювання, відомий під назвою «метод Монте-Карло», - це числовий метод розв'язування задач за допомогою моделювання випадкових величин.

Перша особливість цього методу ‑ простота алгоритму. Як правило, складають програму для одного випробування. Потім цей дослід повторюють N разів, при цьому кожен дослід не залежить від інших. За результатами дослідів визначають середні величини, тому цей метод одержав іншу назву - метод статистичних випробувань.

Друга особливість цього методу - похибка обчислень, як правило, пропорційна , де В - деяка стала. Отже, щоб зменшити похибку у k разів, треба збільшити N у k разів, хоча домогтися високої точності таким шляхом, як правило, неможливо.

Приклад з використанням методу Монте-Карло.