
Тема 2 Етапи прийняття рішень та класифікація задач оптимізації в менеджменті
ЗМІСТ
1. Етапи прийняття рішень 2
2. Класифікація задач оптимізації 3
3. Класифікація методів менеджменту (математичні методи) 6
3.1. Детерміновані ЕММ 7
3.2. Ймовірнісні ЕММ 10
пункт 1: _Глухов_Матем_мет_мод_менеджм2005, стр. 15-17
пункт 2: _Глухов_Матем_мет_мод_менеджм2005, стр. 17-20
пункт 3: Економічні дослідження (методологія, інструментацій, організація, апробація): навч. посіб. ; за ред.. А.А. Мазаракі. – К. : Київ. нац. торг.-екон. Ун-т, 2010. – 280с, стр.192.
(учебник у меня)
1. Етапи прийняття рішень
Розробку будь-якої моделі оптимізації можна приблизно розбити на 5 стадій, частково перекривають один одного і не мають чітких кордонів.
1. Постановка (формулювання) завдання.
2. Розробка математичної моделі досліджуваної системи.
3. Відшукування рішення за допомогою цієї моделі.
4. Перевірка даної моделі й рішення.
5. Уточнення рішення на практиці.
При постановці завдання проводиться передпроектне обстеження об'єкта моделювання, формулюється мета рішення, обмеження, форми вхідної та вихідної інформації, порядок її перетворення і використання і т. д. Порядок прийняття рішень ми можемо простежити по малюнку 1.
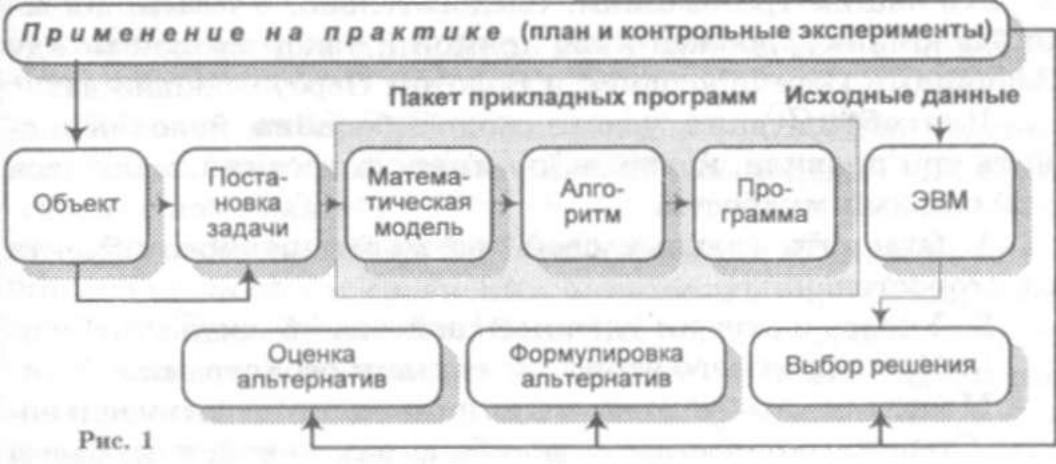
При розробці математичної моделі формалізується мета рішення, з якою пов'язуються змінні величини та готівкові обмеження, оцінюється число можливих (допустимих) варіантів рішення.
Власне рішенням на ЕОМ передує розробка алгоритму - формалізованої послідовності дій по реалізації моделі (блок-схем вирішення задачі), за якою розробляється програма розв'язання задачі на ЕОМ або підбирається готовий програмний продукт.
Далі порівнюється отримане рішення з реальною дійсністю, щоб з'ясувати, чи дійсно вирішена реальна задача, чи всі змінні в моделі враховані, чи всі обмеження формалізовані, чи всі зміни об'єкта внесені в модель і т. д.
Для забезпечення успіху моделювання треба виконати три правила:
1. Відокремити головні властивості модельованого об'єкта від другорядних.
2. Врахувати в моделі головні властивості об'єкта.
3. Знехтувати його другорядними властивостями.
Модель - це умовне уявлення дійсності. Ступінь відповідності може бути різною і проблема полягає в тому, щоб, обираючи рівень спрощення реальної ситуації, залишити основні впливають фактори і співвідношення між ними.
2. Класифікація задач оптимізації
Для постановки задачі прийняття рішення необхідно виконання двох умов:
повинно бути декілька рішень;
варіант повинен бути обраний за певним принципом.
Очевидно, що якщо немає хоча б двох можливих варіантів рішення, то вибирати нема з чого, тому завдання щодо прийняття рішення відсутнє. Наприклад, якщо підприємству задано план, який встановлює номенклатуру і кількість продукції, що випускається, то задачі щодо визначення плану немає, оскільки план заданий.
Відомі два принципи вибору:
вольовий;
критеріальний.
1) Вольовий вибір, найбільш часто використовуваний, застосовують при відсутності формалізованих моделей як єдино можливий.
2) Критеріальний вибір полягає в прийнятті деякого критерію та порівнянні можливих варіантів, які відповідають критерію. Варіант, для якого вибраний критерій приймає найкраще рішення, називають оптимальним (від лат. оptimus), а задачу прийняття найкращого рішення ‑ задачею оптимізації.
Рішення може бути оптимальним тільки за умови обраного критерію, а не оптимальним взагалі.
Критерій оптимізації називають цільовою функцією, функцією мети, функціоналом , тощо.
Будь-яку задачу, рішення якої зводиться до знаходження максимуму або мінімуму цільової функції, називають задачею оптимізації. Задачі менеджменту найчастіше пов'язані з пошуком умовного екстремуму цільової функції при відомих обмеженнях, що накладаються на її змінні.
В якості цільової функції при вирішенні різних оптимізаційних задач приймають кількість чи вартість своєї продукції, витрати на виробництво, суму прибутку і т. п. Обмеження зазвичай - ресурси: людські, матеріальні, грошові.
Оптимізаційні задачі менеджменту (різні за своїм змістом і реалізуються з використанням стандартних програмних продуктів), відповідають тому чи іншому класу економіко-математичних моделей. Класифікацію деяких основних задач оптимізації, реалізованих менеджментом на виробництві, можна виконати за наступними ознаками (табл. 1): функція управління; склад оптимізаційних задач; клас економіко-математичних моделей.
Таблиця 1 Признаки класифікації задач оптимізації реалізованих менеджментом на виробництві
Функції управління |
Задачі оптимізації |
Клас економіко-математичних моделей |
Технічна і організаційна підготовка виробництва |
Моделювання складу виробів. Оптимізація складу сумішей (марок, шихти). Оптимізація розкрою листового матеріалу, прокату. Оптимізація розподілу ресурсів в мережевих моделях комплексів робіт. Оптимізація планування підприємств, виробництва та обладнання. Оптимізація маршруту виготовлення виробів. Оптимізація технологій і технологічних режимів. |
Дискретне (цілочисельне) програмування. Лінійне програмування. Мережеве планування і управління. Імітаційне моделювання. Динамічне програмування. Нелінійне програмування. Теорія графів. |
Техніко-економічне планування |
Побудова зведеного плану та прогнозування показників розвитку підприємства. Оптимізація портфеля замовлень і виробничої програми. Оптимізація розподілу виробничої програми по планових періодах. |
Балансові (матричні) моделі «витрати-випуск». Кореляційно-регресійний аналіз. Екстраполяція тенденцій. Лінійне програмування. |
Оперативне управління основним виробництвом |
Оптимізація календарно-планових нормативів. Календарні завдання. Оптимізація стандарт-планів. Оптимізація короткострокових планів виробництв. |
Нелінійне програмування. Імітаційне моделювання. Лінійне програмування. Цілочисельне програмування. |
Інша важлива ознака систематизації ‑ класифікація моделей за її елементами: вихідні дані, шукані змінні, залежності, що описують мету завдання (моделювання) та обмеження (рис. 2).

Рис. 2 Класифікація моделей за елементами
І. В залежності від вхідних даних виділяють 3 типи математичного опису задач управління:
детерміновані;
імовірнісні;
задачі в умовах невизначеності.
а) Вхідні дані, які задані певними (рус. определенными) величинами, називають детермінованими.
Детерміновані задачі формулюються в умовах повної визначеності про значення використовуваних параметрів, склад і вид обмежуючих умов. Такий опис має однозначність при математичному представленні та дозволяє отримати однозначне рішення.
В детермінованій задачі завжди відомо, що стратегія дій А призведе до результату а, а стратегія дій В - до результату b. Залишається тільки визначити, який результат має більшу корисність, щоб обрати кращу з двох стратегій.
Детерміновані задачі розглядають як граничний варіант задач з ризиком, в яких імовірність появи значень використовуваних параметрів дорівнює одиниці.
Оцінки ймовірностей бувають об'єктивними і суб'єктивними. Об'єктивні ймовірності отримують як відношення числа подій, які нас цікавлять, до загальної кількості спостережуваних подій.
б) Вихідні дані, які залежать від ряду випадкових факторів, називають випадковими величинами.
Наприклад, наявність ресурсів залежить від своєчасності їх постачання і т. д.
Імовірнісні (стохастичні) задачі, включають у постановці задачі параметри, що задаються у вигляді випадкових величин, для яких відомі ймовірності досягнення можливих значень. Такі задачі називають також задачами з ризиком, і їх рішення формулюється як конкретні результати з імовірнісною оцінкою кожного з них.
в) Задачі в умовах невизначеності виникають в ситуаціях, коли немає попередньої ймовірнісної оцінки можливих майбутніх ситуацій або значень параметрів, які їх характеризують. У подібних задачах використовують своєрідний підхід для опису оцінки переваги управлінських стратегій. Оцінка МАКСИМІН припускає перевагу стратегії дій, у якій досягається максимально корисний результат при найбільш несприятливому розвитку подій. Оцінка МІНІМАКС орієнтує на вибір стратегії, що вимагає найменших витрат при найбільш несприятливому розвитку подій.
ІІ. Змінні величини можуть бути безперервними та дискретними. Безперервні величини можуть приймати в заданому інтервалі будь-які значення (наприклад, відсотковий уміст елементів у матеріалі). Дискретні (або цілочисельні), приймають тільки цілі значення (наприклад, не можна ввести в експлуатацію 1,5 будівлі).
ІІІ. Залежності між елементами можуть бути лінійними і нелінійними. Лінійними називають залежності, до яких входять змінні першого ступеня і немає їх добутку (рус. произведение). Нелінійними називають залежності, до яких входять змінні не в першому ступені або є добуток змінних.
Поєднання різних елементів моделі призводить до різних класів задач оптимізації, які вимагають різних методів рішення, отже, і різних програмних засобів (табл. 2).
Початкові дані (исходные данные) |
Змінні |
Залежності |
Задача |
Детерміновані |
Безперервні |
Лінійні |
Лінійного програмування |
Цілочисельні |
Лінійні |
Цілочисельного програмування |
|
Безперервні, цілочисельні |
Нелінійні |
Нелінійного програмування |
|
Випадкові |
Безперервні |
Лінійні |
Стохастичного програмування |
