ДНК - удивительное природное образование со спиральной симмет­рией. Длинные переплетенные нити цепочечной структуры ДНК состоят из молекул сахара и фосфатов. К молекулам сахара присоединяются азотистые основания, образуя поперечные связи между двумя спиральными нитями. Вытянутая молекула ДНК напоминает винтообразную лестницу. Это дейст­вительно макромолекула: ее молекулярная масса может достигать 10⁹ . Не­смотря на сложное строение, молекула ДНК содержит лишь четыре азотис­тых основания: А, Т, С, G. Между аденином и тимином образуются водо­родные связи. Они настолько структурно соответствуют друг другу, что аденин распознает тимин и связывается с ним, и наоборот. Цитозин и гуанин — еще одна пара аналогичного типа. В данных нуклеотидных парах, таким об­разом, А всегда связывается с Т, а С с G (рис. 3.5). Такая связь лежит в ос­нове принципа комплементарности.

Способность азотистых оснований к распознаванию своего партнера приводит к свертыванию сахарофосфатных цепей в виде двойной спирали, которая экспериментально подтверждена в результате рентгеноструктурных наблюдений. Взаимодействия между азотистыми основаниями в высшей сте­пени специфичны, поэтому спираль может сформироваться лишь в случае, если последовательности оснований в обеих цепях полностью идентичны.

Сахарофосфатная группа вместе с азотистым основанием А, Т, С или G называется нуклеотидом (рис. 3.6). Она может рассматриваться как стро­ительный блок. Из таких блоков и состоит молекула ДНК. С помощью пос­ледовательности нуклеотидов кодируется информация в молекуле ДНК. В ней содержится информация, необходимая для производства белков, нужных живому организму.

Молекула ДНК может копироваться в процессе катализируемой фермен­тами репликации, заключающейся в ее удвоении. При репликации происхо­дит разрыв водородных связей и образование одинарных цепей, служащих в качестве матрицы при ферментативном синтезе таких же последовательнос­тей строительных блоков. Процесс репликации включает, т разрыв и формирование водородных связей. В начале репликации две проти­воположные цепи начинают раскручиваться и отделяться одна от другой (рис. 3.7). В точке раскручивания фермент пристраивает новые цепи к двум старым по принципу комплементарности: Т в новой цепи располагается про­тив А в старой и т.д., в результате образуются две идентичные двойные спи­рали.

Вследствие относительной непрочности таких связей репликация про­исходит без нарушения более сильных ковалентных связей в сахарофосфатных цепях. Кодирование генетической информации и репликация молекулы ДНК — взаимосвязанные важнейшие процессы, необходимые для развития живого организма.

Генетическая информация кодируется последовательностью нуклеоти­дов ДНК. Три последовательных нуклеотида составляют единицу генетичес­кого кода, называемую кодоном. Каждый кодон определяет положение одной аминокислоты.

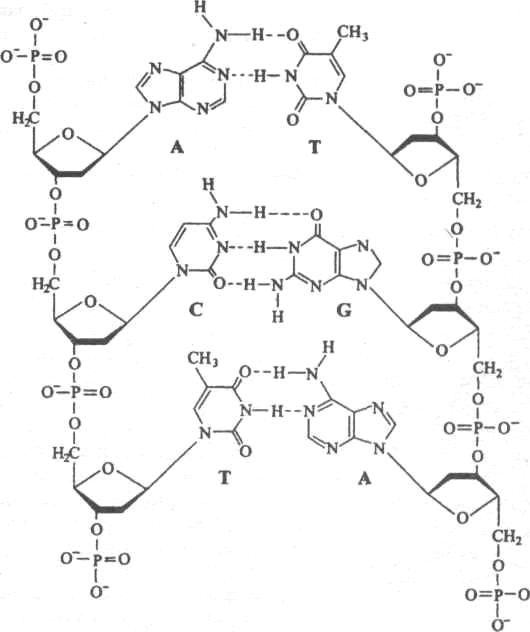
Рис. 3.5. Водородные связи в нуклеотидных парах

Рис. 3.6. Расположение нуклеотида в молекулярной цепи ДНК

Молекулу ДНК можно представить в виде последовательности букв-нуклеотидов, образующих текст из большого их числа, например ACATTGGAG... В таком тексте и содержится информация, определяющая специфику каждого организма: человека, дельфина и т.д.

Генетический код всего живого, будь то растение, животное или бакте­рия, одинаков. Например, кодон GGU во всех организмах кодирует аминокислоту глицин. Такая особенность генетического кода вместе со сходством аминокислотного состава всех белков свидетельствует о биохимическом единстве жизни, которое, по-видимому, отражает происхождение всех живых существ от единого предка.

Белки — это природные органические соединения, состоящие из макро­молекул, молекулярная масса которых от нескольких тысяч до нескольких миллионов.

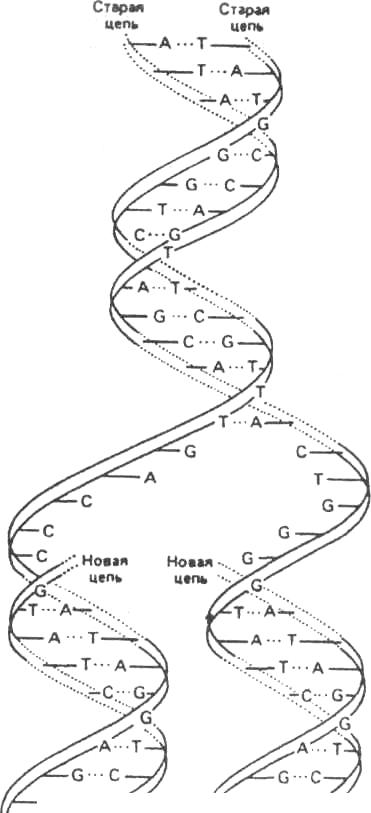Рис. 3.7. Репликация молекулы ДНК.

Белки выполняют множество разнообразных функций. Практически все химические реакции в организме катализируются особым видом белков — ферментами. Белки выполняют роль переносчиков, например гемоглобин переносит кис­лород от легких к тканям. Мышечные сокращения и внутриклеточное дви­жения — результат взаимодействия молекул белков, функция которых заключается ещё и в координации движений. Одна из важных групп белковых молекул — антитела — защищает орга­низм от вирусов, бактерий и т.п. Активность нервной системы зависит от белков, с помощью которых собирается и хранится информация, поступаю­щая из окружающей среды. Группа белков — гормоны управляют ростом клеток и их активностью. Процессы жизнедеятельности живых организмов определяются взаимо­действием двух видов макромолекул — ДНК и белков. Генетическая инфор­мация организма хранится в молекулах ДНК.

Белки производятся с помощью особой молекулы, в которой считывается информация, закодированная в ДНК. Такая молекула называется рибо­нуклеиновой кислотой (РНК). В состав молекулы РНК входят четыре азотис­тых основания, три из них такие же, как и в ДНК: аденин, цитозин, гуанин, а четвертое - урацил (U). Каждая аминокислота кодируется тремя нуклеотидами. Например, последовательность цитозин (С) - аденин (А) - урацил (U), т.е. CAU соответствует аминокислоте гистодину, CUG - лейцину, CCG - пролину, AUG - метионину (рис. 3.8).

В результате большой работы по расшифровке генетического кода, про­водимой в течение нескольких десятилетий, разработаны методы не только определения последовательностей аминокислот в белковых цепях, но и их компоновки в заданном порядке. В лаборатории удалось получить таким об­разом полипептиды и даже небольшие белки, идентичные тем, что выделены из природных источников. К настоящему времени разработаны два эффек­тивных метода синтеза гена, что весьма важно для развития биотехнологии. В одном из них под действием дегидратирующих агентов проводится фосфоролирование сахаров. В другом предварительно синтезируется промежуточная структура для получения заданной скелетной фосфатной связи.

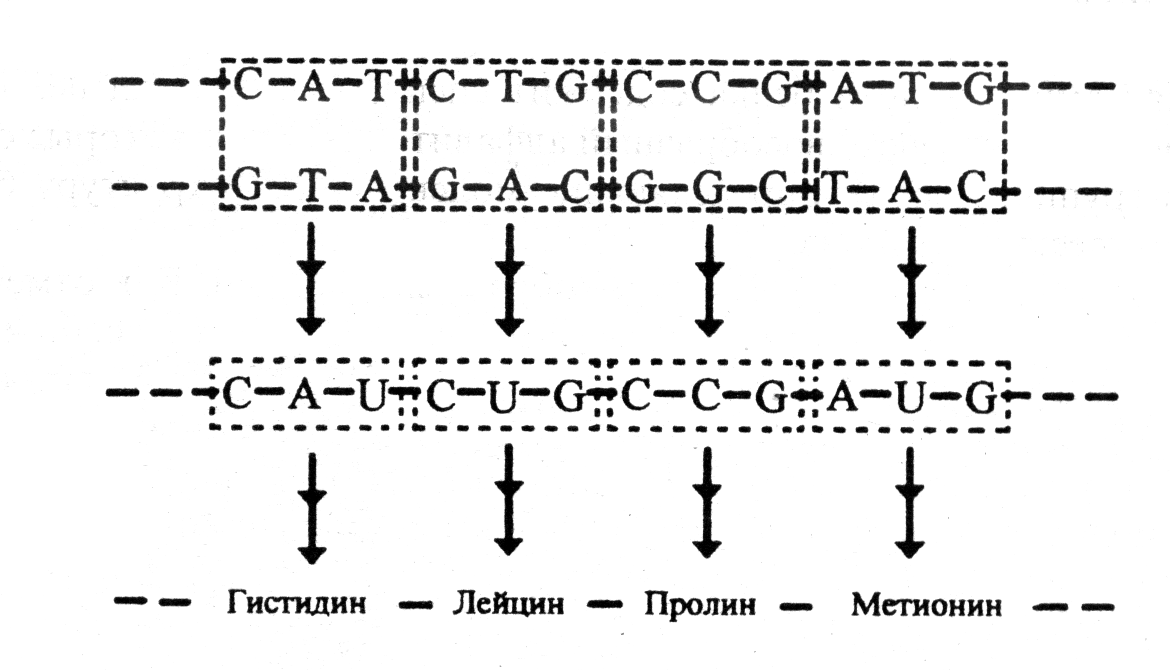
Рис. 3.8. Образование нуклеотидных групп молекулы ДНК.

5.3. Физика колебаний, волновые явления. Циклические процессы жизнедеятельности как колебательный

процесс

Колебаниями называются движения или процессы, которые характеризуются определенной повторяемостью во времени. Колебательные процессы широко распространены в природе и технике, например качание маятника часов, переменный электрический ток и т.д. При колебательном движении маятника изменяется координата его центра масс, в случае переменного тока колеблются напряжение и ток в цепи. Физическая природа колебаний может быть разной, поэтому различают колебания механические, электромагнитные и др. Различные колебательные процессы описываются одинаковыми характеристиками и одинаковыми уравнениями. Отсюда следует целесообразность единого подхода к изучению колебаний различной физической природе.

Колебания называются свободными (или собственными), если они совершаются за счет первоначально сообщенной энергии при последующем отсутствии внешних воздействий на колебательную систему. Простейшим типом колебаний являются гармонические колебания - колебания, при которых колеблющаяся величина изменяется со временем по закону синуса (косинуса).

Рассмотрение гармонических колебаний важно по двум причинам: 1) колебания, встречающиеся в природе и технике, часто имеют характер, близкий к гармоническому; 2) различные периодические процессы (процессы, повторяющиеся через равные промежутки времени) можно представить как наложение гармонических колебаний. Гармонические колебания величины s описываются уравнением типа

, (5.1)

где: А - максимальное значение колеблющейся величины, называемое амплитудой колебания, - круговая (циклическая) частота, -начальная фаза колебаний в момент времени t=0, ( - фаза колебаний в момент времени t. Фаза колебаний определяет значение колеблющейся величины в данный момент времени. Фаза колебаний определяет значение колеблющейся величины в данный момент времени. Так как косинус изменяется в пределах от +1 до –1, то s может принимать значения от +А до –А.

Определенные состояния системы, совершающей гармонические колебания, повторяются через промежуток времени Т, называемый периодом колебаний, за который фаза получает приращение 2 , т.е

;

откуда Т=2 (5.2)

Величина, обратная периоду колебаний,

, (5.3)

т.е. число полных колебаний, совершаемых в единицу времени, называется частотой колебаний. Сравнивая (5.2) и (5.3), получим

Единица частоты - герц (Гц): 1 Гц- частота периодического процесса, при котором за 1 с совершается один цикл процесса.

Запишем первую и вторую производные по времени от гармонически колеблющейся величины s:

; (5.4)

, (5.5)

т.е. имеем гармонические колебания с той же циклической частотой. Амплитуды величин (5.4) и (5.5) соответственно равны А и А . Фаза величины (5.4) отличается от фазы (5.1) на , а фаза величины (5.5) отличается от фазы (5.1) на . Следовательно, в моменты времени, когда s=0, ds/dt приобретает максимальное положительное значение (рис.5.1).

Из выражения (5.5) можно получить дифференциальное уравнение гармонических колебаний:

(5.6)

Решением этого уравнения является выражение:

s=А cos ( + ).

механические гармонические колебания

Пусть материальная точка совершает гармонические колебания вдоль оси х около положения равновесия, принятого за начало координат. Тогда зависимость х от времени t задается уравнением, аналогичным уравнению (5.1):

х = A cos ( ), (5.7)

Согласно выражениям (5.4) и (5.5), скорость и ускорение колеблющейся точки соответственно равны

(5.8)

Сила , действующая на колеблющуюся материальную точку массой m, с учетом (5.7) и (5.8) равна

F = - m х

Следовательно, сила пропорциональна смещению материальной точки из положения равновесия и направлена в противоположную сторону (к положению равновесия).

Кинетическая энергия материальной точки, совершающей прямо-линейные гармонические колебания, равна:

Т= (5.9)

или Т= (5.10)

Потенциальная энергия материальной точки, совершающей гармонические колебания под действием упругой силы F, равна

, (5.11)

или (5.12)

Сложив (5.9) и (5.11), получим формулу для полной энергии:

(5.13)

Так как амплитуда и частота колебаний есть постоянные величины (для незатухающих колебаний), из последнего выражения видно, что энергия колебательной системы остается постоянной с течением времени.

Наглядными моделями колебательных механических систем являются пружинный, и математический маятники. Они оба - гармонические осцилляторы, колебания которых описываются уравнением вида:

(5.14)

Пружинный маятник-это груз массой m, подвешенный на абсолютно упругой пружине и совершающий гармонические колебания под действием упругой силы F= - kx, где k-жескость пружины. Уравнение движения такого маятника , или

Из выражений (3.14) и (3.1) следует , что пружинный маятник совершает гармонические колебания по закону х = А с циклической частотой

(5.15)

и периодом (5.16)

Формула (5.15) справедлива для упругих колебаний в пределах выполнения закона Гука, т.е. когда масса пружины мала по сравнению с массой тела. Потенциальная энергия пружинного маятника, согласно (5.11) и (5.15), равна

Математический маятник- это идеализированная система, состоящая из материальной точки массой m , подвешенной на длинной, тонкой, нерастяжимой, невесомой нити, и колеблющаяся под действием силы тяжести. Хорошим приближением математического маятника является небольшой тяжелый шарик, подвешенный на тонкой длинной нити.

Момент инерции математического маятника

, (5.17)

где: l- длина маятника.

Предположив, что математический маятник это частный случай физического маятника, с массой, сосредоточенной в центре тяжести тела, можно получить выражение для периода малых колебаний математического маятника.

(5.18)

Волновые процессы. Продольные и поперечные волны.

Процесс распространения колебаний в сплошной среде называется волновым процессом (или волной). При распространении волны частицы среды не движутся вместе с волной, а колеблются около своих положений равновесия. Вместе с волной от частицы к частице среды передается лишь состояние колебательного движения и его энергия. Поэтому, основным свойством всех волн, независимо от их природы, является перенос энергии без переноса вещества.

Среди разнообразия волн, встречающихся в природе и технике, выделяются следующие их типы: волны на поверхности жидкости, упругие и электромагнитные волны. Упругими (или механическими) волнами называются механические возмущения, распространяющиеся в упругой среде. Упругие волны бывают продольные и поперечные. В продольных волнах частицы среды колеблются в направлении распространения волны, в поперечных – в плоскостях, перпендикулярных направлению распространения волны.

Расстояние между ближайшими частицами, колеблющимся в одинаковой фазе, называется длиной волны . Длина волны равна тому расстоянию, на которое распространяется определенная фаза колебаний за период, т.е.

или учитывая, что Т =1/ , где - частота колебаний,

Бегущими волнами называются волны, которые переносят в пространстве энергию. Перенос энергии волнами количественно характеризуется вектором плотности потока энергии. Этот вектор для упругих волн называется вектором Умова (по имени русского ученого Н.А. Умова (1846-1915), решившего задачу о распространении энергии в среде). Направление вектора Умова совпадает с направлением переноса энергии, а его модуль равен энергии, переносимой волной за единицу времени через единичную площадку, расположенную перпендикулярно направлению распространения волны.

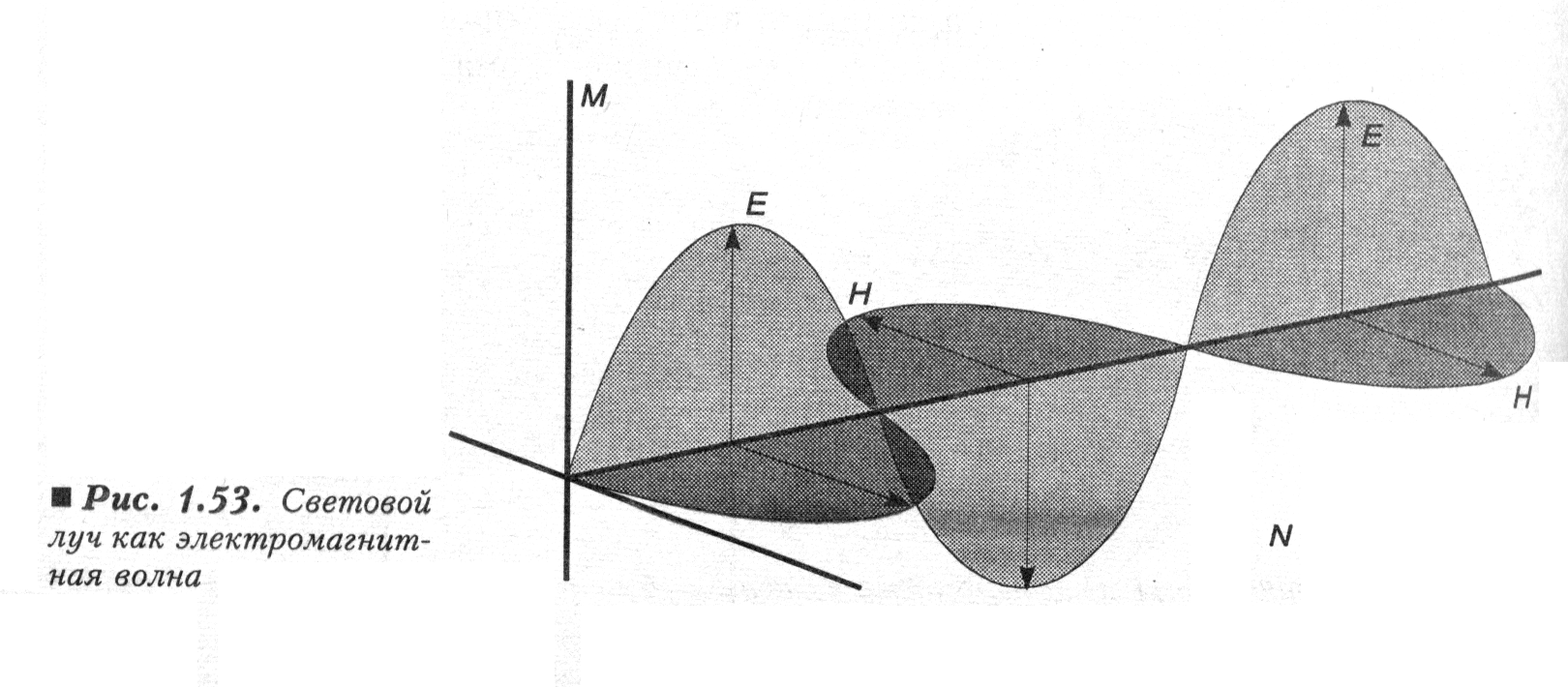Пример схематичного движения электромагнитной волны представлен на рис. 3.9. На нём видно, что волновой вектор (как и вектор скорости волны) направлен вдоль оси абсцисс, а вдоль Y и Z ко-леблются вектора напряжён-ности электрического ( ) и магнитного ( ) п олей.

Рис. 3.9. Схема распространения электромагнитной волны.

Для вывода уравнения бегущей волны - зависимости смещения колеблющейся частицы от координат и времени - рассмотрим плоскую волну, предполагая, что колебания носят гармонический характер, а ось х совпадает с направлением распространения волны. В данном случае волновые поверхности перпендикулярны оси х, а так как все точки волновой поверхности колеблются одинаково, то смещение будет зависеть только от координаты х и t, т.е. (х, t). Для некоторой точки среды, находящейся на расстоянии х от источника колебаний, их уравнение запишется выражением

(5.19)

где: , а - скорость распространения волны.

Следовательно, является не только периодической функцией времени, но и периодической функцией координаты х. Уравнение (5.19) есть уравнение бегущей волны. Если плоская волна распространяется в противоположном направлении, то

В общем случае уравнение плоской волны, распространяющейся вдоль положительного направления оси х в среде, не поглощающей энергию, имеет вид

, (5.20)

где: А = const- амплитуда волны, - циклическая частота, - начальная фаза волны, определяемая в общем случае выбором начал отсчета x и t, - фаза плоской волны.

Для характеристики волн используется волновое число

(5.21)

Учитывая (5.20), уравнению (5.21) можно придать вид

(5.22)

Уравнение волны, распространяющейся вдоль отрицательного направления оси х, отличается от (5.22) только знаком члена kx.

Если среда, в которой распространяется одновременно несколько волн, линейна, т.е. ее свойства не изменяются под действием возмущений, создаваемых волной, то к ним применим принцип суперпозиции (наложения) волн: при распространении в линейной среде нескольких волн каждая из них распространяется так, как будто другие волны отсутствуют, а результирующее смещение частиц среды в любой момент времени равно геометрической сумме смещений, которые получают частицы, участвуя в каждом из слагающих волновых процессов.

Исходя из принципа суперпозиции и разложения Фурье любая волна может быть представлена в виде суммы гармонических волн, т.е. в виде волнового пакета, или группы волн. Волновым пакетом называется суперпозиция волн, мало отличающихся друг от друга по частоте, занимающая в каждый момент времени ограниченную область пространства.

В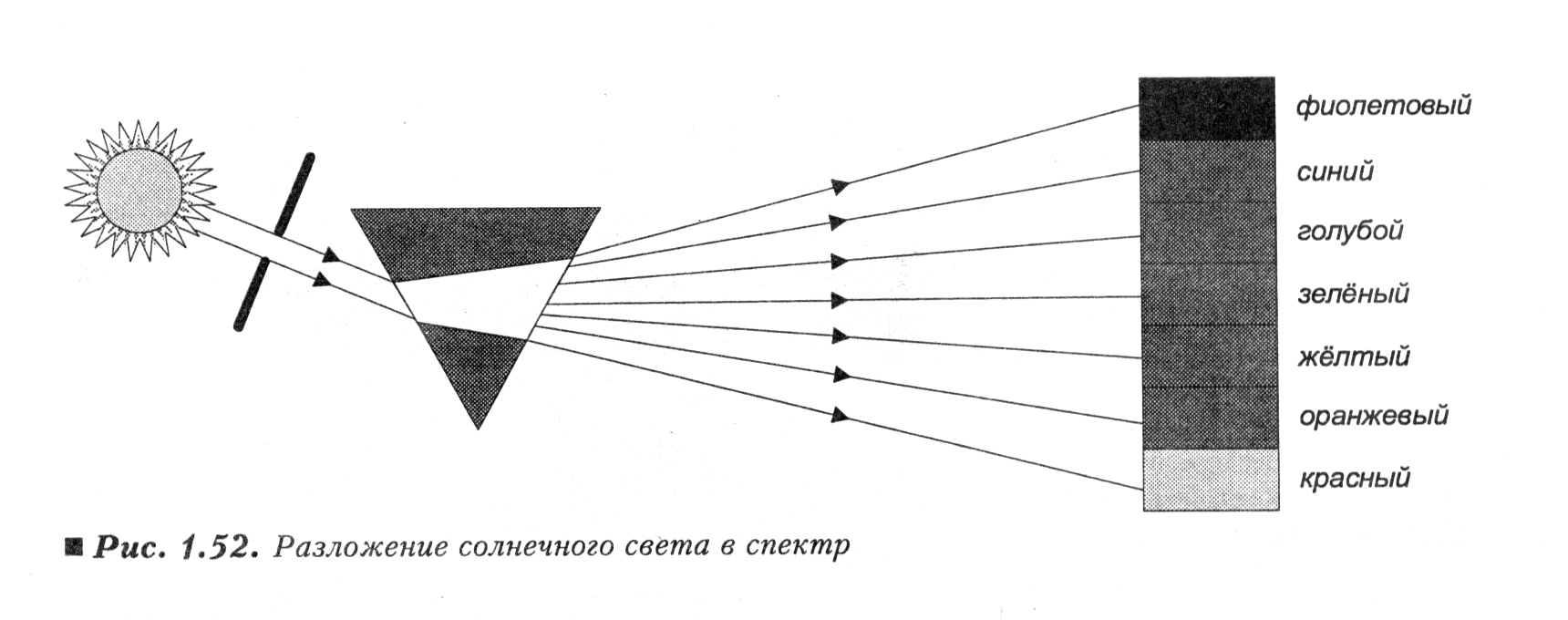 том случае, если волна распространяется в среде, её скорость определяется значениями скорости распространения. Обычно, чем выше

Рис. 3.10. Наблюдение дисперсии света с помощью призмы.

скорость света в среде, тем больше длина волны в ней. За счёт зависимости коэффициента преломления света от длины волны на границе прозрачных сред наблюдается явление дисперсии (“разложения” белого света в спектр). Пример дисперсии света представлен на рис.3.10. Попадая на призму белый свет, состоящий из набора семи основных монохроматических цветов, преломляется. Так как длины волн отдельных цветов различны, разные значения имеют и коэффициенты преломления. Следовательно, на экране наблюдается дисперсионный спектр.

Наиболее наглядно волновые процессы можно наблюдать на звуковых волнах. Звуковыми (или акустическими) волнами называются распространяющиеся в среде упругие волны, обладающие частотами в пределах 16 - 20 000 Гц. Волны указанных частот воздействуя на слуховой аппарат человека, вызывают ощущение звука. Волны с   16 Гц (инфразвуковые) и   20 кГц (ультразвуковые) органами слуха человека не воспринимаются.

Совершая колебания, тело вызывает колебания прилегающих к нему частиц среды с такой же частотой. Состояние колебательного движения последовательно передается к все более удаленным от тела частицам, т.е. в среде распространяется волна с частотой колебаний, равной частоте колебаний источника, и с определенной скоростью, зависящей от плотности и упругих свойств среды. Скорость распространения звуковых волн в газах вычисляется по формуле

(5.23)

где: R – молярная газовая постоянная, M- молярная масса, - отношение молярных теплоемкостей газа при постоянных давлении и обьеме, Т –термодинамическая температура. Из формулы (3.23) вытекает, что скорость звука в газе не зависит от давления р газа, но возрастает с повышением температуры. Чем больше молярная масса газа, тем меньше в нем скорость звука. Например, при Т =273 К скорость звука в воздухе (М =29  кг/моль) 331 м/с, в водороде (  кг/моль), = 1260 м/с.

При распространении звука в атмосфере необходимо учитывать целый ряд факторов: скорость и направление ветра, влажность воздуха, молекулярную структуру газовой среды, явление преломления и отражения звука на границе двух сред.

Эффект Доплера.

Если источник и приемник движутся относительно друг друга, частота колебаний, воспринимаемых приемником может быть определена из выражения: , (5.24)

причем верхний знак берется, если источник и приемник сближаются, нижний знак - в случае их взаимного удаления.

Ультразвук и его применение.

Ультразвуки широко используются в технике, например для направленной подводной сигнализации, обнаружения подводных предметов и определения глубин ( гидролокатор, эхолот). Например, в эхолоте от пьезокварцевого генератора, укрепленного на судне, посылают направленные ультразвуковые сигналы, которые, достигнув дна, отражаются от неге и возвращаются обратно. Зная скорость распространения в воде и определяя время прохождения (от подачи до возвращения) ультразвукового сигнала, можно вычислить глубину. Прием эха также производится с помощью пьезокварца. Звуковые колебания, дойдя до пьезокварца, вызывают в нем упругие колебания, в результате чего на противоположных поверхностях кварца возникают электрические заряды, которые измеряются.

Получение электромагнитных волн.

Существование электромагнитных волн - переменного электромагнит-ного поля, распространяющегося в пространстве с конечной скоростью,- вытекает из уравнений Максвелла. Уравнение Максвелла сформулированы в 1865г. на основе обобщения эмпирических законов электрических и магнитных явлений. Как уже указывалось, решающую роль для утверждения максвелловской теории сыграли опыты Герца (1888), доказавшие, что электрические и магнитные поля действительно распространяются в виде волн, поведение которых полностью описывается уравнениями Максвелла.

Источником электромагнитных волн в действительности может быть любой электрический колебательный контур или проводник, по которому течет переменный электрический ток, так как для возбуждения электромагнитных волн необходимо создать в пространстве переменное электрическое поле (ток смещения) или соответственно переменное магнитное поле. Однако излучающая способность источника определяется его формой, размерами и частотой колебаний. Чтобы излучение играло заметную роль, необходимо увеличить объем пространства, в котором переменное электромагнитное поле создается. Поэтому для получения электромагнитных волн непригодны закрытые колебательные контуры, а так как в них электрическое поле сосредоточено между обкладками конденсатора, а магнитное - внутри катушки индуктивности.

Г ерц в своих опытах, уменьшая число витков катушки и площадь пластин конденсатора, а так же раздвигая их, совершил переход от закрытого колебательного контура к открытому колебательному контору (вибратору Герца), представляющему собой два стержня, разделенных искровым промежутком. Если в закрытом колебательном контуре переменное электрическое поле сосредоточено внутри конденсатора, то в открытом оно заполняет окружающее контур пространство, что существенно повышает интенсивность электромагнитного излучения. Колебания в такой системе поддерживается за счет источника .э.д.с, подключенного к обкладкам конденсатора, а искровой промежуток применяется Рис. 3.11. Схема работы лазера. для того, чтобы увеличить разность

потенциалов, до которой первоначально заряжаются обкладки.

На рис. 3.11 представлена схема работы твердотельного лазера. Рассматриваемый материал является типичным примером трёхуровневой квантовой системы. За счёт наличия дискретных энергетических уровней и разных времён жизни на них элементарных частиц, возможно накопление энергии и экспрессное её высвобождение (в виде электромагнитного импульса).

Циклические процессы жизнедеятельности, как колебательный процесс

Жизнедеятельность практически всех организмов подчиняется цикличности. Наиболее просто данный факт можно наблюдать на примере суточных изменений на Земле. За 24 часа Земля поворачивается на 360⁰ вокруг своей оси. При этом наблюдается последовательная смена утра, дня, вечера, ночи. Известно, что для большинства растений, особенно использующих процесс фотосинтеза, обязательна дневная фаза, когда они освещаются Солнцем. Подавляющее большинство животных и насекомых также бодрствуют днем. Однако, значительна доля растений, насекомых, животных, ведущих ночной образ жизни. Понятно, что суточная смена необходима для осуществления процессов жизнедеятельности и тех, и других. Наглядно циклический суточный процесс можно наблюдать и на примере такого вида живого как человек. И работа, и отдых, и учеба, и воспитание, и военная служба, и наряды – все это осуществляется циклично, с определенной периодичностью. Известно, что даже функционирование отдельных органов, содержание в них необходимых химических веществ связано с временем суток.

Не менее важно, и не менее заметно проявление цикличности, связанной с движением Земли по орбите, которое проявляется как смена времен года. В данном случае циклические проявления еще более заметны. В умеренных широтах ярко выражены зима, весна, лето, осень с соответствующими характерными для растительности, птиц, животных признаками. Меняется и поведение человека, хотя, следует отметить такую особенность, как сглаживание зависимости его от внешних факторов, связанное прежде всего с обладанием энергией, информацией, веществом.

В значительной степени все мы находимся под влиянием Космоса, что косвенно проявляется в попытках человека предсказывать будущее через астрологические прогнозы.

Человек, как часть природы, живет по циклическим законам. Следовательно, практически его любой процесс представим как колебательный, циклический. Приняв этот аргумент, можно более точно предвидеть и оценивать складывающуюся ситуацию и более правильно, адекватно на нее реагировать. В конечном итоге, осознание цикличности процессов помогает проведению более верных, необходимых данной системе процессов самоорганизации.