Замена переменной и интегрирование по частям. Для определенного интеграла, как и неопределенного, имеют место формулы замены переменной и интегрирования по частям.
Теорема 22. Пусть выполняются следующие условия:
функция f(x) определена и непрерывна на отрезке [a,b];
функция x=g(t) имеет непрерывную производную на [α,β],
3) [a,b] = [g(α),g(β)];
Тогда справедлива формула замены переменных в определенном интеграле
.
□ Пусть
Ф(х)
некоторая первообразная f(x),
тогда 
Т.к. Ф(х) и g(t) дифференцируемы, то правилу дифференцирования сложных функций имеем
.
Отсюда следует, что функция Ф(g(t)) является на [α,β] первообразной для f(g(t))g’(t). Тогда по формуле Ньютона-Лейбница:
.
Т.к. g(α)=a g(β)=b то, приравнивая, получим
.
■
Пример
21.
Вычислить
.
Решение.
Рассмотрим подстановку
,
.
Проверим законность такой подстановки.
Во-первых, функция
непрерывна на
;
во-вторых, функция
дифференцируема на
и
непрерывна на
и, в-третьих, при изменении t
от 0 до
функция
изменяется от 0 до 1, причем
и
.
Таким образом, данная подстановка
удовлетворяет всем условиям теоремы
22. Применяя формулу замены переменных,
получаем
.
Замечание. При использовании формулы замены переменных необходимо проверять выполнение перечисленных в теореме условий. Если эти условия нарушаются, то может быть получен и неверный результат.
Пример 22. Вычислить интеграл
.
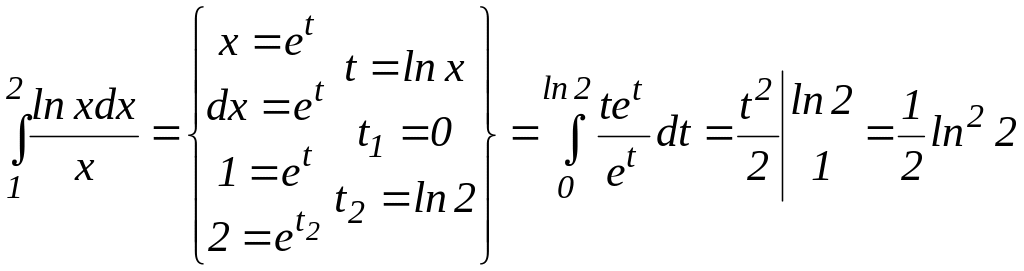Теорема 23. Пусть функции u(x) и v(x) непрерывны и имеют непрерывные производные на отрезке [a,b]. Тогда справедлива формула интегрирования по частям для определенных интегралов:
или
.
□ Функция u(x)v(x) является первообразной для функции u(x)v’(x)+v(x)u’(x), поэтому
.
Отсюда по свойству определенных интегралов имеем
. ■
Пример
23.
Вычислить
.
□ Положим
;
отсюда
и по формуле интегрирования по частям
находим
■
Пример 24. Вычислить интеграл:
.
6.7. Геометрические приложения определённого интеграла
Теорема 24 (Вычисление площади области в декартовой системе координат). Если f(x) определена, непрерывна и неотрицательна на отрезке [a,b], то площадь множества P={(x,y): a≤x≤b, 0≤y≤f(x)} выражается формулой:
(16)
Множество Р называется криволинейной трапецией, порожденной графиком функции f(x) на [a,b].
□ Пусть
Т={x0,x1,…,xn}
некоторое разбиение [a,b].
Обозначим ∆xi=xi-xi-1; ∆i=[xi-1,xi]; h(T)=
;
mi=
f(x); Mi=
f(x) (i=1,2…n).
Также обозначим p(T), P(T) – множества, составленные из прямоугольников
pi(T)={(x,y):
xi-1≤x≤xi,
0≤y≤mi,
i=1,n}
(17)
Pi(T)={(x,y):
xi-1≤x≤xi,
0≤y≤Mi,
(18)
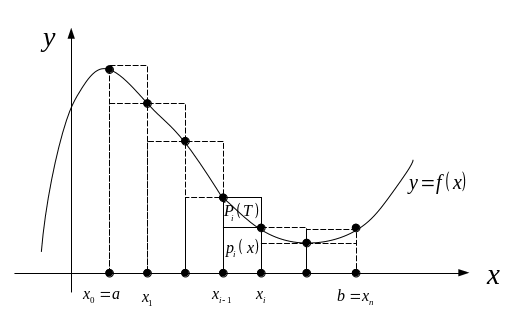
Рис.2
Поскольку
,
для любого разбиения T
имеют место неравенства
μ(p(T))≤μ(P)≤μP(T). (19)
.Из (17) и (18) получим, что
Отсюда,
т.к. прямоугольники 
и 
не имеют общих внутренних точек:
;
.
Следовательно,
площади многоугольников p(T)
и P(T)
равны соответственно нижней и верхним
суммам Дарбу функции f(x)
на [a,b].
Поэтому из (19) следует, что 
.
Но, т.к. f(x)
непрерывна на [a,b],
то она интегрируема на этом отрезке, а
следовательно
.
По критерию интегрируемости верхний и нижний интеграл Дарбу совпадают и равны интегралу от f(x) по [a,b](см. замечание к критерию интегрируемости). Переходя к пределу при h(T)→0 в неравенствах (19), получим
.
■
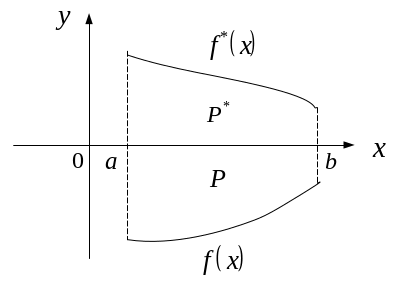
Рис.3
Следствие 1. Если f(x) непрерывна и неположительная на отрезке [a,b] и P={(x,y): a≤x≤b, f(x)≤y≤0}, то
.
(20)
□ Положим f*(x)=-f(x)≥0 => множество P* симметрично множеству P относительно оси Ox. Тогда в силу (16):
.
Но μ(P*)=μ(P), тогда => (20). ■ Следствие 2. Формулы (16) и (20) можно объединить в одну формулу. Если f(x) непрерывна и знакопеременна на [a,b] , то площадь множества, заключенного между графиком функции и осью OX равна:
.
Пример 25. Вычислить площадь, образованную одной аркой синусоиды.
□ Область имеет вид (рис.4)
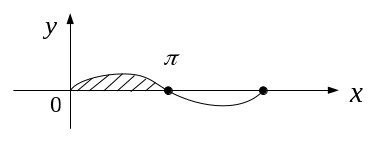
Рис.4
■
Пример
26.
Вычислить площадь множества, ограниченного
эллипсом.
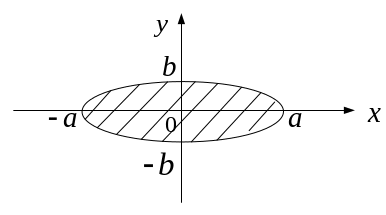
Рис.5
□ Из канонического уравнения эллипса имеем:
Тогда площадь будет равна:
.
■
Следствие
3.
Если функции f(x)
и g(x)
определены и непрерывны на [a,b],
причем f(x)≥g(x)
x
[a,b],
то площадь области P,
заключенной между графиками функций
f(x),
g(x)
и прямыми x=a,
x=b
, равна:
.
(21)
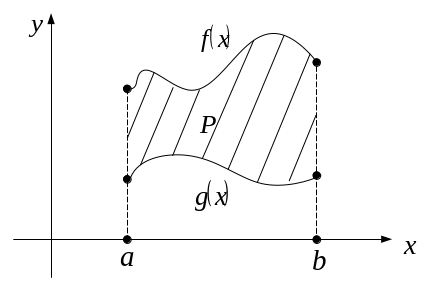
Рис.6
□ Пусть сначала f(x)≥g(x); f(x)≥0 и g(x)≥0. По теореме, площадь множества Р равна разности площадей криволинейных трапеций, порожденных графиками f(x) и g(x)
.
Отсюда,
учитывая линейное свойство интегралов,
получается формула (21). Теперь пусть
f(x)
и g(x)
имеют произвольные знаки на [a,b],
но f(x)≤g(x)
x
[a,b].
Пусть
.Сделаем
замену: y’=y+A
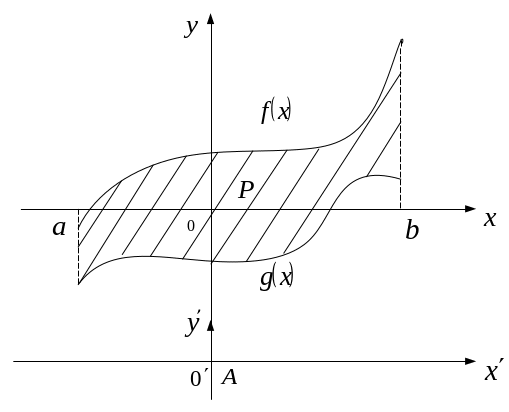
Рис. 7
В системе координат (x, y’) площадь фигуры ограниченную функциями f(x)+A и g(x)+A назовем P’.
Ясно, что P’=P. Вычислим μ(Р’) в (x,y’), учитывая, что f(x)+A≥0 и g(x)+A≥0, по формуле (21) имеем:
Но,
т.к. μ(P)=
,
то
.
■
Пример 27. Найти площадь области, ограниченной кривыми y=x и y=x2-2.
□ Найдем точки пересечения кривых.
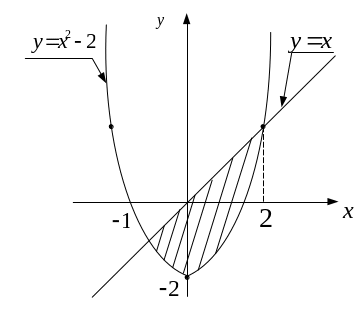
Рис.8
Приравнивая
ординаты, получим: x2-2=x
Тогда площадь будет равна
.
■
Теорема 25. (Вычисление площади множества в полярной системе координат) Если функция r(φ) определена и непрерывна на отрезке [α,β], то площадь множества P={(φ,r): α≤φ≤β, 0≤r≤r(φ)}, граница которой в полярной системе координат задана графиком r(φ) и лучами φ=α и φ=β (которые могут превращаться в точки) определяется по формуле:
(22)
□ Возьмем
разбиение T={φ0,
φ1….
φn}
отрезка [α,β],
где φ0=α,
φn=β,
и положим ∆φi=
φi-
φi-1,
∆i=[
φi-1,
φi],
mi=inf
r(φ)
, Mi=sup
r(φ),
где φ
∆i
и
h(T)=
.
Выберем произвольные точки
.
Тогда pi(T)={(φ,r):
φi-1≤φ≤φi,
0≤r≤mi}
и Pi(T)={(φ,r):
φi-1≤φ≤φi,
0≤r≤Mi}
круговые секторы с углом ∆φi,
i=1,2….n
и радиусами mi
и Mi.
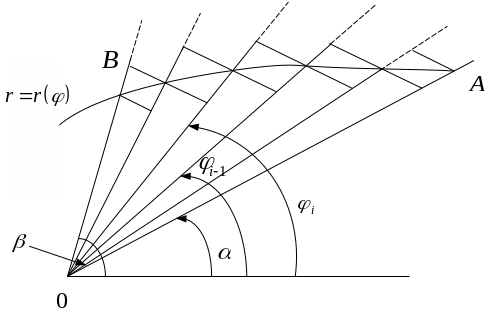
Рис.8
Обозначим
ступенчатые фигуры, составленные из
секторов pi(T)
и Pi(T),
соответственно вписанные в P
и описанные около множества Т.
Тогда
p(T) P P(T) => μ(pT)≤μ(P)≤μ(PT).
По
формуле для площади сектора имеем:
Поэтому
Здесь
s(T)
и S(T)
– суммы Дарбу для функции 
.
Тогда выполняется неравенство
,
(23)где
-
интегральная
сумма для функции
на
отрезке
.
Так как функция
непрерывна на
,
то
тоже
непрерывна и интегрируема на [a,b],
а следовательно, выполняется критерий
.
Переходя
в (23)
к пределу при
,
по
теореме сравнения получим, что справедлива
формула (22).
■
Пример
28.
Найти площадь множества Р,
ограниченного кривой
,
которая называется кардиоидой
.
Теорема
26.
(Вычисление площади множества,
ограниченного кривой, заданной
параметрически ) Площадь множества,
ограниченного простой гладкой замкнутой
кривой
,
заданной параметрическими уравнениями
причем
,
определяется по формуле
(
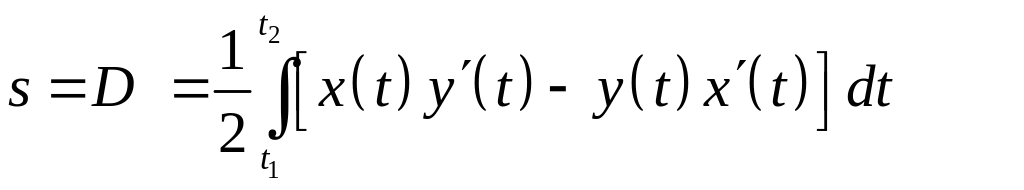23)
Рис.9.
Для
доказательства воспользуемся формулой
(22). Рассмотрим полярную систему координат.
Пусть А и С крайние точки
,
соответствующие полярным координатам
и
,
причем точке А соответствует значение
параметра
начало кривой Г, а значение
- соответствуют точке В – конец замкнутой
кривой Г. Пусть
соответствуют точке С. Из параметрических
уравнений кривой Г и уравнений полярных
координат в декартовой системе координат
имеем
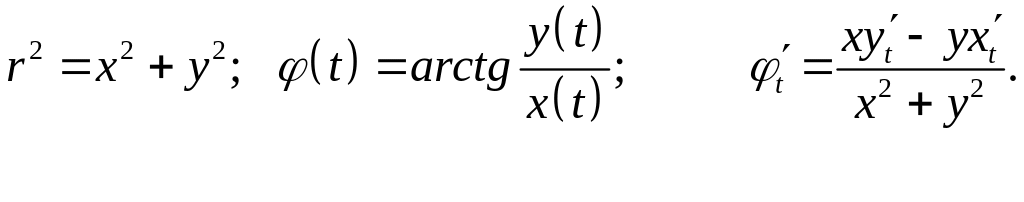Площадь
в полярной системе координат равна
разности площадей двух криволинейных
секторов
и
.
По формуле (22) имеем, предполагая, что
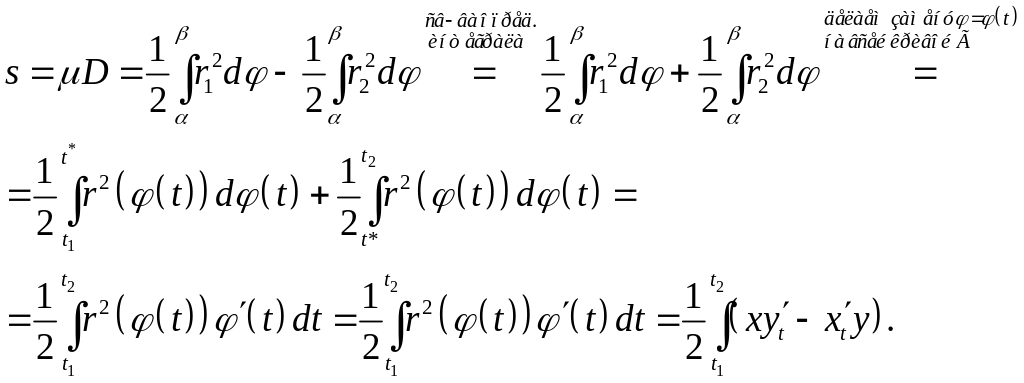
В силу симметрии формула часто приводит к более простым выкладкам при вычислении интегралов. ■
Пример 29. Вычислить площадь, ограниченную эллипсом пользуясь формулой (22).
Решение.
Уравнение
эллипса имеет вид:
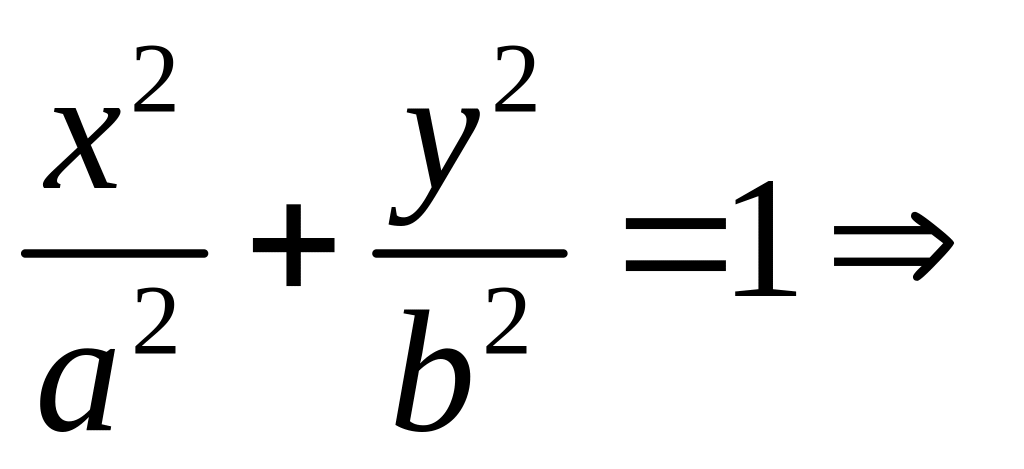параметрезуем
это уравнение
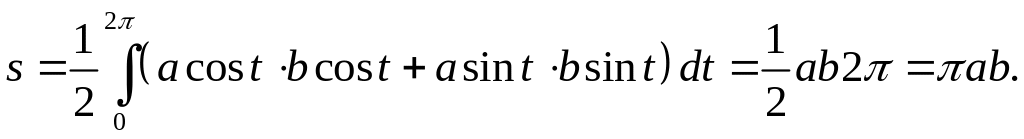
Вычисление
длины кривой.
Пусть Г – кривая на плоскости или в
пространстве, заданная непрерывно
дифференцируемой вектор-функцией
По
определению, длиной кривой называется
верхняя грань длин всевозможных ломанных
вписанных в эту кривую, т.е.
и, если
,
то кривая называется спрямляемой,
и имеет конечную длину, Переменная длина
дуги кривой
,
отсчитываемая от начала кривой Г,
является возрастающей непрерывно
дифференцируемой функцией параметра
и ее производная равна
.
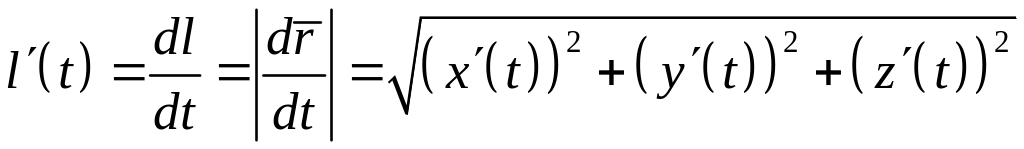Тогда длина кривой Г будет равна
.
По формуле Ньютона-Лейбница имеем
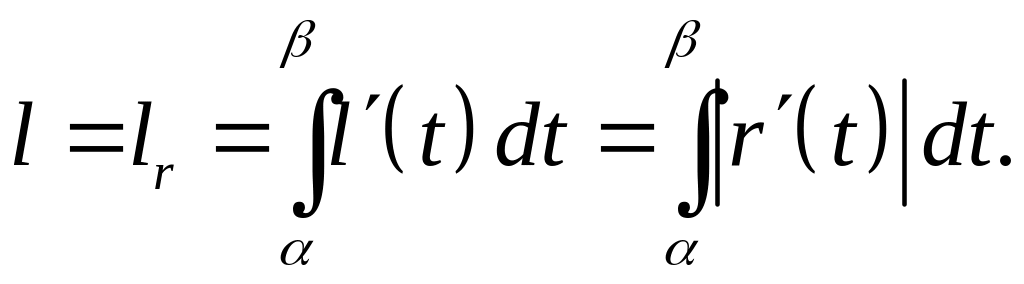
а) Если Г пространственная кривая, то
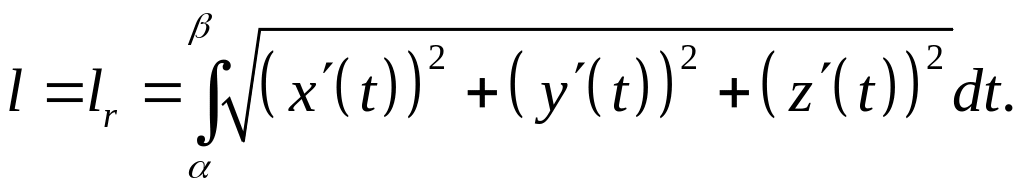
б)
Если Г – плоская кривая, заданная
параметрически
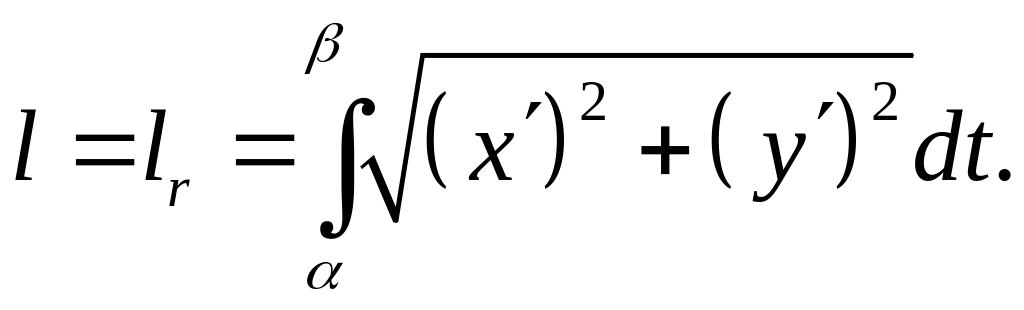(24)
в)
Если Г кривая является графиком функции
на
,
то параметризуя ее
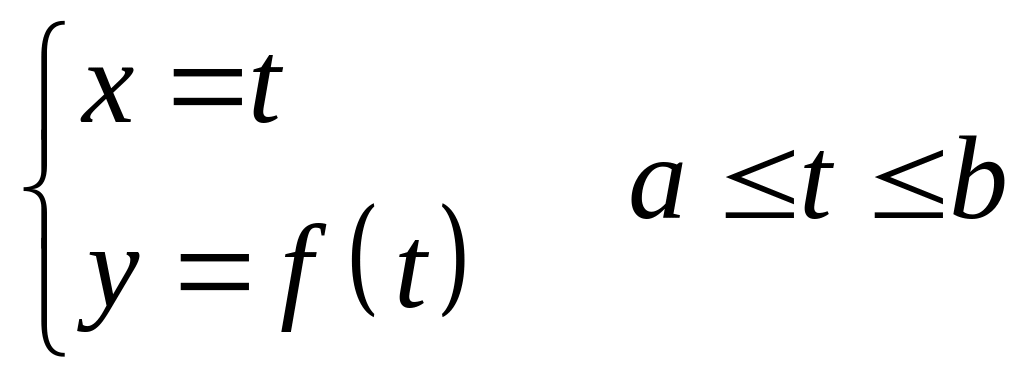из (24) будем иметь:
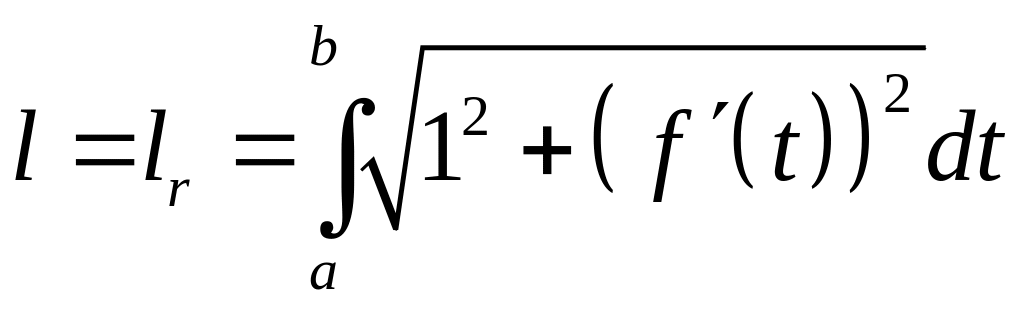или
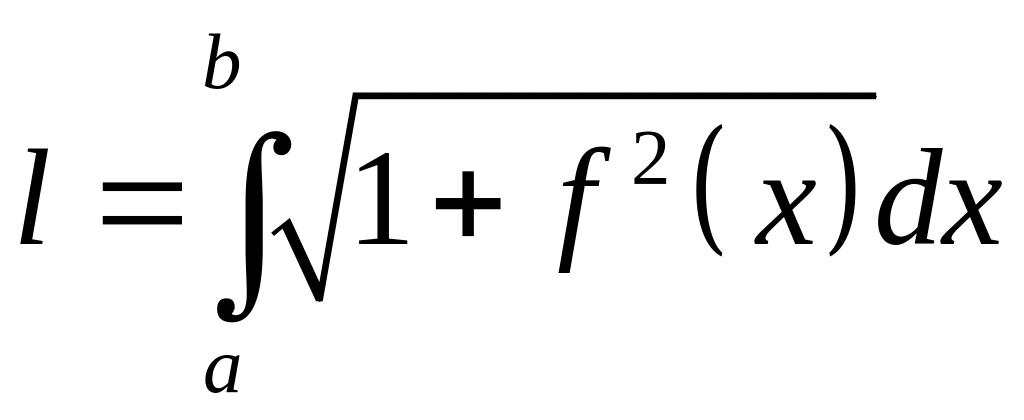(25)
г)
Пусть кривая Г задана в полярной системе
координат уравнением
,
причем функции
и
,
непрерывны на
.
Эту
кривую можно параметризовать, используя
связь декартовой системы координат и
полярной, приняв за параметр угол
:
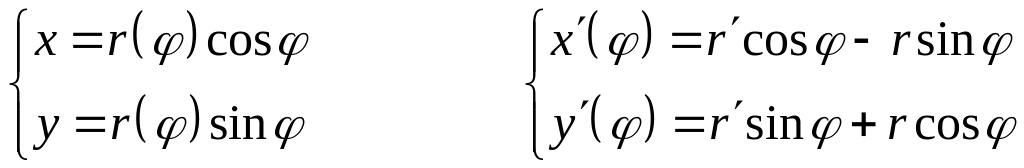
Подставим в (24), после преобразований, получим
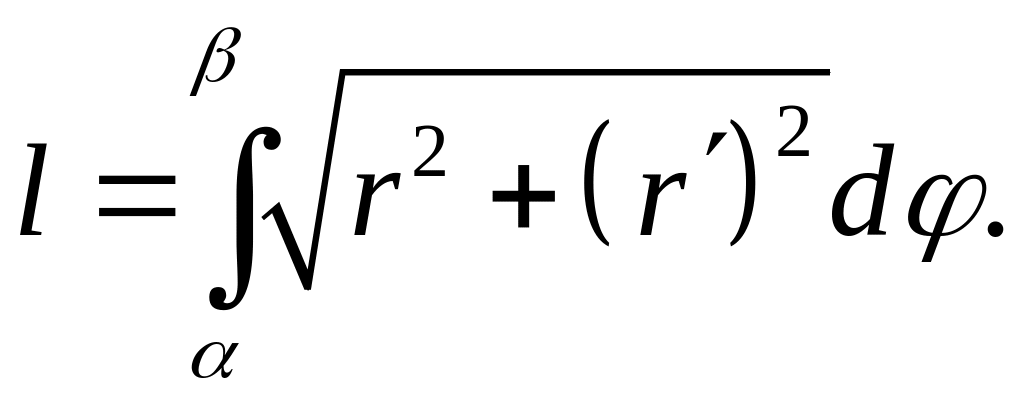(26)
Пример
30.
Вычислить длину дуги верхней ветви
полукубической параболы
,
если
.
Решение
.
Из уравнения
находим:
Следовательно, по формуле (25) получим
Пример
31.
Вычислить длину дуги одной арки циклоиды
.
Решение. Из уравнений циклоиды находим:
Когда
пробегает отрезок
параметр
пробегает отрезок
.
Следовательно, искомая длина дуги будет
равна:
Пример
32.
Вычислить длину первого витка спирали
Архимеда:
.
Решение.
Первый виток спирали образуется при
изменении полярного угла
от 0 до
.
Поэтому по формуле (26) искомая длина
дуги равна
Теорема27.
(Вычисление
объема
тела вращения).
Пусть
функция
непрерывна и неотрицательна на отрезке
.
Тогда тело, которое образуется вращением
вокруг оси
криволинейной трапеции, ограниченной
сверху графиком функции
,
имеет объем
.
(27)
□
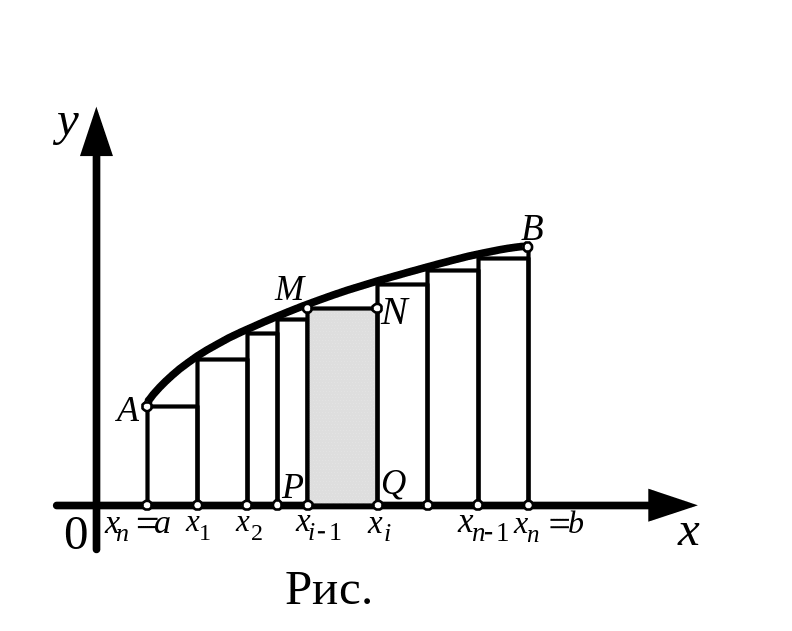Рассмотрим
разбиение отрезка
на
частей точками
.
На каждом частичном отрезке
возьмем точки
и построим прямоугольник MNPQ
(рис.
10).
При вращение вокруг оси
каждый прямоугольник опишет цилиндр.
Найдем объем
цилиндра, образованного вращением
прямоугольника
:
,
где
.
Сумма объемов всех цилиндров приближенно равна объему данного тела вращения:
.
С
другой стороны, эта сумма является
интегральной суммой для интеграла (27).
Так как функция
непрерывна на
,
то предел этой суммы при
существует и равен определенному
интегралу (27). Таким образом,
. ■
Пример
33.
Найти объем тела, полученного вращением
эллипса
вокруг оси Оу.
Решение.
.
Пример
34.
Вычислить объем тора. (Тором называется
тело, получающееся при вращении круга
радиуса
вокруг оси, лежащей в его плоскости на
расстоянии
от центра круга
.
Форму тора имеет, например, баранка).
Решение.
Пусть круг вращается вокруг оси
(рис. 11). Объем тора можно представить
как разность объемов тел, полученных
от вращения криволинейных трапеций
и
вокруг оси
.
У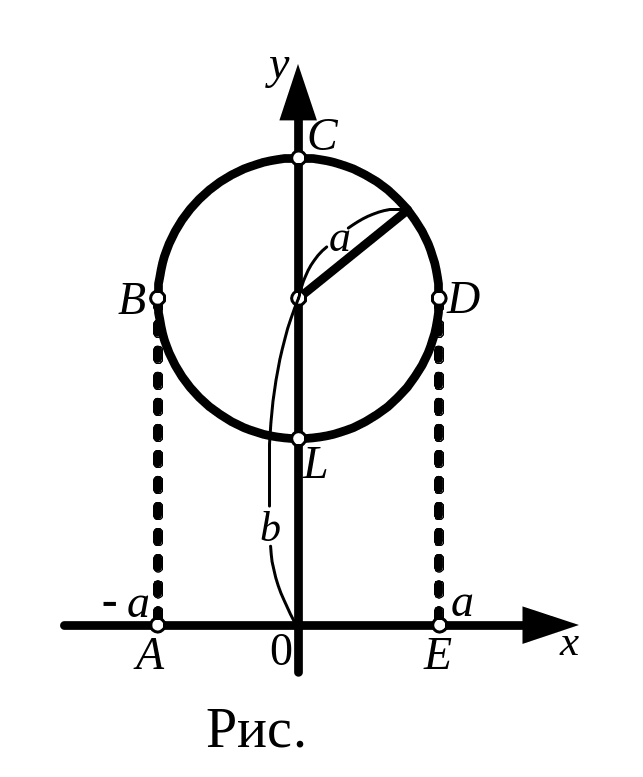
равнение
окружности
имеет вид
,
причем
уравнение кривой
,
а
уравнение кривой
,
Используя формулу (27), получаем для объема тора выражение
.
Теорема28. (Вычисление площади поверхности вращения). Пусть функция неотрицательна и непрерывна вместе со своей первой производной на отрезке . Тогда поверхность, образованная вращением графика этой функции вокруг оси , имеет площадь, которая может быть вычислена по формуле
. (28)
□ Разобьем
произвольный отрезок
на
частей точками
.
Пусть
,
,
,…,
,
,…,
– соответствующие точки графика функции
.
Построим ломанную
,
,
,…,
(рис. 12). При вращении этой ломанной
вокруг оси
получим поверхность, составленную из
боковых п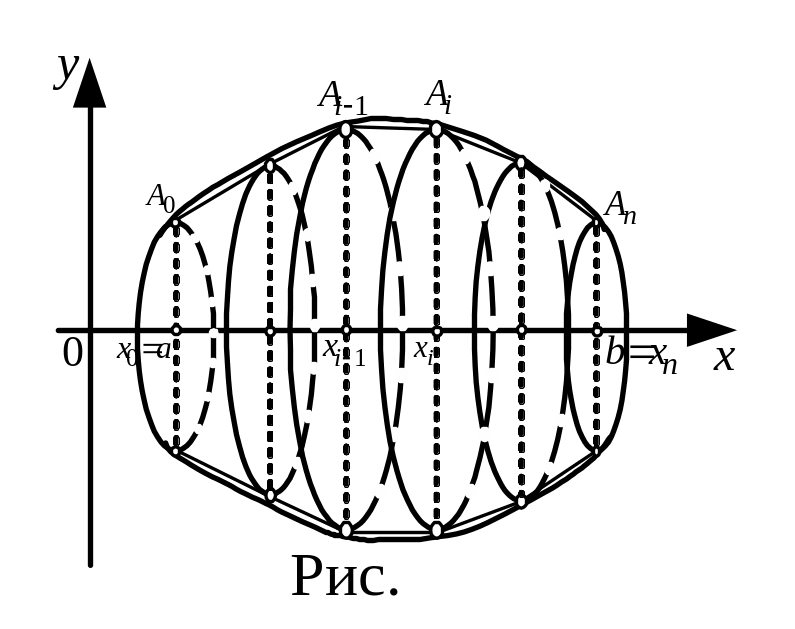
оверхностей
усеченных конусов (цилиндров). Площадь
боковой поверхности усеченного конуса
(цилиндра), образованного вращением
звена ломаной, равна
– длина хорды
,
,
т.е.
.
По формуле Лагранжа
.
Полагая
,
получаем
.
Итак, площадь поверхности вращения приближенно равна площади поверхности, полученной от вращения ломанной
.
Представим эту сумму в виде двух сумм
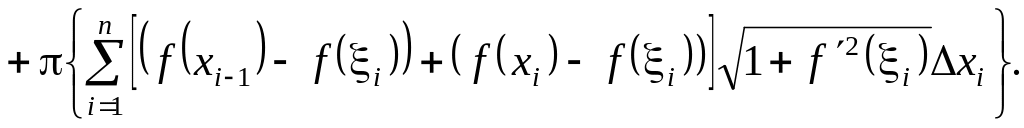(29)
Первая
сумма в правой части последнего равенства
является интегральной суммой для
интеграла (28), и при
в силу непрерывности функции
имеет своим пределом этот интеграл.
Покажем, что выражение в фигурных скобках
в правой части равенства (29) имеет при
предел, равный нулю. Действительно, так
как функция
равномерно-непрерывна на
,
то по теореме Кантора для любого
существует
такое, что при
выполняются неравенства
и
.
Если обозначить через
максимальное значение функции
на отрезке
,
то выражение в фигурных скобках при
оценивается следующим образом:
.
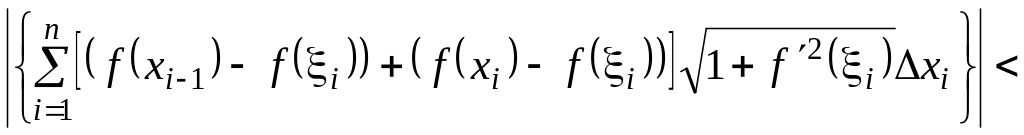
Так
как
произвольно мало, то отсюда следует,
что предел указанного выражения равен
нулю при
.
Таким образом, переходя в равенстве (29) к пределу при , имеем , т.е. получена искомая формула (28). ■
Замечание.
Если поверхность получается вращением
вокруг оси
кривой
,
заданной параметрическими уравнениями
,
,
,
причем
,
изменяется от
до
при изменении
от
до
,
,
,
то, производя в интеграле (28) замену
переменной
,
получаем
. (30)
Наконец,
если кривая задана уравнением в полярных
координатах:
,
,
где
имеет непрерывную производную на
,
то этот случай сводится к параметрическому
заданию кривой
,
,
,
и формула (30) принимает вид
.
Пример
35.
Вычислить площадь поверхности шарового
пояса, образованного вращением
полуокружности
,
,
вокруг оси
.
Решение. По формуле (28) получаем
,
где
– высота пояса.
Пример
36.
Вычислить площадь поверхности, полученной
вращением одной арки циклоиды
,
,
,
вокруг оси
Решение. По формуле (30) имеем
.