6.5. Определённый интеграл (Интеграл Римана)

Определение интеграла по Риману. Рассмотрим некоторый отрезок [a,b] R. Множество точек называется разбиением отрезка [a,b]. Разбиение будем обозначать буквой Т([a,b]) . Число будем называть максимальным шагом или просто шагом разбиения Т. Очевидно, и .

Пусть функция f(x) определена на отрезке [a, b], Т – разбиение отрезка [a, b]. Для каждого i выберем произвольную точку , i= . Выражение называется интегральной суммой для функции f(x) при данном разбиении Т и выбранных точках (i= 1, 2, … , n).

Определение 3. Функция f(x) называется интегрируемой по Риману на отрезке [a, b] если существует конечный предел I интегральных сумм при стремлении к нулю шага разбиения h(T), при любом разбиении Т отрезка [a, b] и независимо от выбора точек .

Этот предел называется интегралом Римана или определенным интегралом. Обозначение:

.

Предел понимается в том смысле, что число точек разбиения Т неограниченно растёт при h→0, а выбраны произвольным образом.

Пример 19. Если , то .

Теорема 4. Если функция f(x) интегрируема на отрезке [a, b], то она ограничена на этом отрезке.

□ Предположим противное, т.е. f(x) интегрируема, но неограниченна на отрезке [a, b]. Пусть – произвольное положительное число. Тогда по определению 3, существует δ=δ(ε) с шагом h(T)< δ(ε) и выполняется неравенство

или

Отсюда следует, что множество интегральных сумм с этим шагом разбиения ограниченно. Выберем одно из разбиений. Т.к. по предположению f(x) неограниченна на [a, b], то существует отрезок на котором f(x) неограниченна. За счёт выбора точки слагаемое , а вместе с ним и вся интегральная сумма может быть сделана сколь угодно большой. Последнее, однако, не возможно, поскольку множество интегральных сумм с шагом h(T) < δ(ε) ограничено. Получили противоречие. ■

Суммы Дарбу и их свойства Пусть f(x) ограниченная на отрезке [a,b] функция. - некоторое разбиение отрезка [a, b]. Введём следующие обозначения:

; ;

; ;

; . (3)

Суммы S(T) и s(T) называются соответственно верхней и нижней суммой Дарбу. Очевидно, что : , следовательно

s(T) ≤ или s(T) ≤ σ(T) ≤ S(T) . (4)

Вспомним определение точных верхней и нижней граней.

β = sup X: 1) ;

2) x X: β-ε < x ≤ β;

α = inf X: 1) x ≥ α;

2) x X: x < α+ε;

sup X - наименьшее среди всех чисел, ограничивающих множество сверху.

inf X – наибольшее среди всех чисел, ограничивающих множество снизу.

Заметим, что s(T) и S(T) могут не совпадать ни с какими интегральными суммами. Это связано с тем, что f(x) может не принимать и на .

Определение 4. Разбиение Т' отрезка [a,b] называется измельчением разбиения Т, если каждая точка разбиения Т содержится среди точек разбиения Т'. Обозначение Т Т'.

Пусть и два разбиения отрезка [a, b]. Будем обозначать разбиение, образованное точками разбиений и . Докажем следующие свойства сумм Дарбу.

Свойство 1. Пусть f(x) определена на [a, b] и Т исходное разбиение отрезка, тогда справедливы равенства:

.

□ Пусть ε произвольное положительное число. Поскольку , то . Тогда, по определению точной верхней грани существуют такие , что:

(b-a) ;

i=1,2…n.

Просуммировав эти неравенства, умножаем на и получим:

< ≤ или

S(T) – ε < ≤ S(T) , следовательно S(T) = . ■

Аналогично доказывается второе равенство.

Свойство 2. Пусть Т Т', причём Т' получено из Т добавлением р новых точек деления. Тогда имеют место следующие неравенства:

, (5)

т.е. , но и это означает, что , т.е. верхние суммы Дарбу не возрастают при измельчении разбиения Т, а нижние не убывают на множестве разбиений Т.

□ Поскольку любое измельчение разбиения Т может быть получено последовательным добавлением новых точек разбиения, то свойство достаточно проверить, когда Т ' получено добавлением одной точки х'. Пусть .

Очевидно, что

, (6)

Тогда .

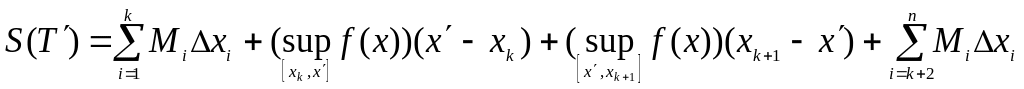Отсюда следует, что

.

Из полученного соотношения в силу неравенств (6) имеем

.

Для р точек справедливость неравенства следует из того, что при добавлении новой точки последняя оценка удваивается. Аналогично доказываться второе неравенство (5). ■

Свойство 3. Для любых двух разбиений , отрезка и , т.е. любая нижняя сумма Дарбу не превосходит любую верхнюю сумму Дарбу.

□ Пусть , два произвольных разбиения, тогда

.

В силу свойства 2 и неравенств (4) будем иметь

. ■

Согласно этому свойству, нижние суммы Дарбу ограничены сверху, а верхние – снизу. Поэтому существуют точные нижняя и верхняя грани на множестве всех разбиений Т. Обозначим , , причем очевидно, что

. (7)

Это неравенство следует из свойств 3 и 2 и определения sup и inf. Числа и называют верхними и нижними интегралами Дарбу.

Лемма Дарбу. Для произвольного найдется такое число , что с шагом выполняется неравенство

. (8)

Справедливость формулы (8) следует из определения sup и inf, а так же и .

Теорема 5. (Критерий интегрируемости функции). Для того, чтобы ограниченная функция f(x) была интегрируема на необходимо и достаточно, чтобы такое, чтобы выполнялось неравенство:

, (9)

т.е. чтобы существовал предел

.

□ Необходимость. Пусть функция f(x) интегрируема на , -произвольное положительное число. Тогда, по определению 1, , что для любого разбиения Т и при любом наборе точек выполняется неравенство

или .

В силу свойства 1 и неравенства (4) справедливы неравенства , тогда ;

Отсюда следует, что для любого разбиения Т с шагом имеет место неравенство: .

Достаточность. Пусть ε – произвольное положительное число и выполняется неравенство (9) при некотором разбиении Т.Из неравенств (8) и (9) следует:

=> => .

В силу произвольности ε , это возможно лишь когда . По лемме Дарбу с шагом выполняется неравенство: . Из полученного неравенства, в силу (4) следует, что при любом выборе точек получим:

=> . Т.е. функция f(x) интегрируема на отрезке . ■

Очевидно, что неравенство (9) можно записать в виде

или ,

где - колебание функции на отрезке .

Из доказательства теоремы следует, что для того, чтобы функция f(x) была интегрируема на , необходимо и достаточно, чтобы ее верхний и нижний интегралы Дарбу совпадали, т.е. .