6.4. Интегрирование иррациональных и трансцендентных функций
Предварительно
введем обозначение рациональной функции
от двух переменных
и
,
т. е. функции, получающейся из двух
переменных
и
и некоторых постоянных, над которыми
производятся только операции сложения,
вычитания, умножения и деления:
Такова, например, функция
Если
переменные
и
,
в свою очередь, являются функция;
переменной
:
,
то функция
называется рациональной функцией от
и
.
Например, функция
является
рациональной функцией от
и от
;
здесь
,
а функция
является
рациональной функцией от
и от
:
Рассмотрим теперь интегралы от некоторых простейших иррациональных и трансцендентных функций и покажем, что в ряде случаев они сводятся к интегралам от рациональных функций (или, как говорят, рационализируются) и могут быть вычислены методами рассмотренными ранее.
1.
Интеграл вида
,
где
— некоторые числа
;
— натуральное число,
— рациональная функция от
и от
.
Покажем, что такой интеграл рационализируется
подстановкой
.
В самом деле,
так что
где
— рациональная функция аргумента
.
Пример
11.
Вычислить
□ Сделав
подстановку
получим
Далее, имеем
■
Пример
12. Вычислить
□
■
Пример
13.
.
□ Положим
,
откуда
.
Следовательно,
.
■
2.
Интеграл вида
,
где
— некоторые
числа;
– рациональная
функция переменных
и
Если
трехчлен
имеет вещественные корни
и
,
то
Следовательно,
т. е. получаем интеграл, рассмотренный в п. 1.
Если
,то
т. е. под знаком интеграла находится рациональная функция от .
Поэтому
интересен случай, когда трехчлен
не имеет вещественных корней и
.
Покажем, что в данном случае интеграл
рационализируется подстановкой
Эйлера:
.
Возводя
обе части равенства
в квадрат, получаем
так
что
,
,
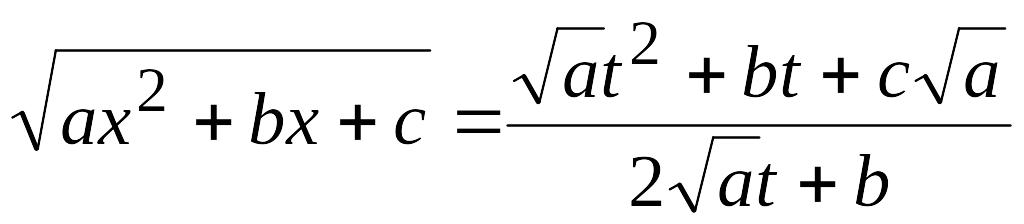Таким образом,
,
где
– рациональная функция от
.
Если
же в трехчлене
,
а
,
то для рационализации интеграла можно
применить другую подстановку Эйлера:
.
Пример
14.
Вычислить
.
□ Поскольку
трехчлен
имеет комплексные корни, сделаем
подстановку
.
Возводя обе части равенства в квадрат,
получаем
или
;
отсюда
,
.
Тогда
.
Далее, имеем
.
Умножая
обе части равенства на
,
получаем
,
или
.
Приравнивая
коэффициенты при одинаковых степенях
,
получаем систему уравнений первой
степени относительно
:
откуда
.
Следовательно,
,
и окончательно
.
■
Пример
15.
Вычислить
.
□ Здесь
трехчлен
имеет комплексные корни и
,
,
поэтому воспользуемся подстановкой
.
Возводя обе части равенства в квадрат,
получаем
или
;
отсюда
,
,
.
Таким образом,
.■
Заметим, что вычисление интегралов с помощью подстановок Эйлера обычно приводит к громоздким выражениям и трудоемким выкладкам, поэтому их следует применять, только если данный интеграл не удается вычислить более коротким способом.
3.
Интеграл вида
,
где
– рациональная функция от
и от
.
Покажем, что интеграл рационализируется
подстановкой
,
которая называется универсальной
тригонометрической подстановкой.
Действительно,
,
,
,
так что
,
где
– рациональная функция t.
Пример
16.
Вычислить
.
□ Применяя
подстановку
,
получаем
,
,
.
Таким образом,
.
■
Пример
17.
.
□ Положим
.
Тогда
,
и
,
где
.
■
Пример
18.
.
□ В
данном случае проще вычислить интеграл,
не прибегая к подстановкам и представив
подынтегральную функцию в виде
.
Тогда
.
■
В заключение отметим, что рассмотренные методы и приемы интегрирования не исчерпывают всех классов аналитически интегрируемых элементарных функций. В то же время из всего изложенного следует, что техника интегрирования сложнее по сравнению с дифференцированием. Необходимы определенные навыки и изобретательность, которые приобретаются на практике в результате решения большого числа примеров.