6.3. Рішення задачі про розподіл ресурсів з економічним аналізом отриманих результатів.

Завдання.

Даними в таблиці представлена задача розподілу ресурсів для 4-х видів продукції.

Таблиця.

Дані задачі розподілу ресурсів.

Обсяг ресурсів: трудових, матеріальних, верстатних	Норми витрат ресурсів на од. продукції				Нова продукція
	П-1	П-2	П-3	П-4	П-5
3000	3	4	4	5	5
5000	2	0	3	4	6
8000	10	12	10	8	9
Ціна од. продукції	46	12	10	8	50

Потрібно:

1. побудувати моделі вихідної і двоїстої задач і знайти їхнього рішення ;

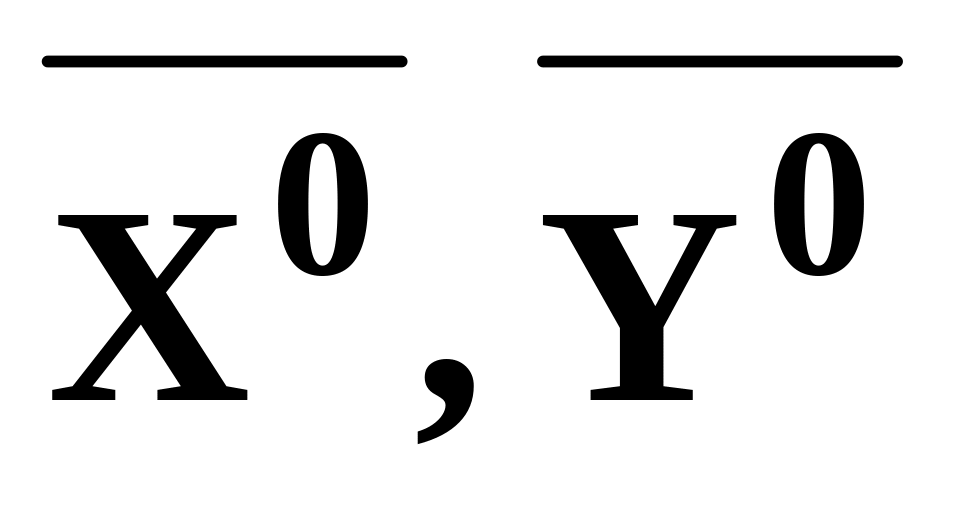2. дати економічне тлумачення основним і додатковим перемінної обох задач;

3. установити діапазони зміни вихідних даних по ресурсах і цінам одиниці продукції, при яких структура оптимального плану не міняється;

4. проаналізувати доцільність розширення асортименту продукції за рахунок включення нової продукції П-5.

Рішення

1. Складемо математичні моделі вихідної та двоїстої задач, позначивши через план випуску j-го виду продукції, а через вартість за одиницю i-го ресурсу. Тоді за формулами (47-48), (49-50) математичні моделі вихідної і двоїстої задач мають вид:

вихідна задача двоїста задача

max=46X₁+12X₂+10X₃+8X₄ min f =3000У₁+5000У₂+8000У₃

3X₁+4X₂+4X₃+5X₄≤3000 3У₁+2У₂+10У₃≥46

2X₁+3X₃+4X₄≤5000 4У₁+12У₃≥12

10X₁+12X₂+10X₃+8X₄≤8000 4У₁+3У₂+10У₃≥10

5У₁+4У₂+8У₃≥8

X_j0 Y_i0

Для рішення симплекс-методом перейдемо в обмеженнях до рівностей шляхом уведення додаткових перемінних

вихідна задача двоїста задача

max=46X₁+12X₂+10X₃+8X₄+0(X₅+X₆+X₇) min f =3000У₁+5000У₂+8000У₃

3X₁+4X₂+4X₃+5X₄+X₅ =4000 3У₁+2У₂+10У_3-У4 =46

2X₁+3X₃+4X₄+X₆ =5000 4У₁+12У_3-У5 =12

10X₁+12X₂+10X₃+8X₄+X₇ =8000 4У₁+3У₂+10У_3-У6 =10

5У₁+4У₂+8У_3-У7 =8

X_j0 Y_i0

У вихідної задачі 7 змінних і 3 обмеження, причому додаткові змінні є базисними. Тому цю задачу відразу можна вирішувати симплексом-методом. У двоїстої задачі 7 змінних і 4 обмеження, причому для рішення симплексом-методом треба вводити штучний базис, а це ще плюс 4 змінні. Тому вихідну задачу вирішувати простіше. Запишемо її дані в симплекс-таблицю і проведемо рішення за алгоритмом симплексного методу. У результаті після однієї ітерації перерахування таблиці одержали в оцінному рядку всі ∆j≥0. Виходить, отриманий опорний план вихідної задачі X₁=800; X₂=X₃=X₄=0; X₅=600; X₆=3400; X₇=0, оптимальний.

Цей план випуску продукції =(800;0;0;0;600;3400;0) забезпечує її максимальну сумарну вартість max Z = 36800 ден. ед.

Базис. перем.		Cb	Xb	46	12	10	8	0	0	0	Θo
				X1	X2	X3	X4	X5	X6	X7
X5		0	3000	3	4	4	5	1	0	0	1000
X6		0	5000	2	0	3	4	0	1	0	2500
X7		0	8000	10	12	10	8	0	0	1	800
Z =			0	-46	-12	-10	-8	1	0	0
X5	0		600	0	0.4	1	2.6	0	1	-0.3
X6	0		3400	0	-2.4	1	2.4	0	1	-0.2
X1	46		800	1	1.2	1	0.8	0	0	0.1
Z =			36800	0	43.2	36	28.8	0	0	4.6
				У4	У5	У6	У7	У1	У2	У3

2. Для того, щоб знайти оптимальний план двоїстої задачі, визначимо взаємозв'язок змінних двоїстих задач і економічний зміст їх додаткових змінних. Для вихідної задачі i-а додаткова змінна (47)

(58)

залишок i-го ресурсу для опорного плану вихідної задачі i-а перемінна двоїстої задачі означає ціну за одиницю цього ресурсу.

Для двоїстої задачі j-а додаткова змінна (49)

(59)

різниця між сумарною вартістю витрат усіх ресурсів y_m+1 на одиницю j-го виду продукції та вартості за одиницю цієї продукції. Тому (j=1,…,n) можна трактувати як характеристику рентабельності випуску j-го виду продукції. Якщо y_m+j>0 випуск не рентабельний (витрати більші за ціну), якщо y_m+j=0 випуск j-го виду продукції рентабельний. У силу за вищевикладеним основним змінній однієї задачі відповідають додаткові змінні інший, тобто

(60)

Xn+i Yi

Ym+i Xi

Причому для оптимальних планів цих задач за теоремами 9 з (56), (57) випливає, що

(56)

(57)

З огляду на те, що всі змінні ненегативно з (56`) і (57`) одержимо для оптимальних планів

X⁰_n+i=0 y⁰_i>0 чи X⁰n+i>0 Y⁰_i=0

Y⁰m+j=0 X⁰_j>0 чи Y⁰m+j>0 X⁰_j=0 (61)

З (61) випливає: для оптимальних планів двоїстих задач,

1) якщо i-ий ресурс цілком використовується (X⁰n+i=0) , те його ціна Y⁰i>0, якщо немає (X⁰n+i>0) , те його ціна y⁰_i=0, (j=1,…,m):

2) якщо витрати на випуск одиниці j-го виду продукції більше її ціни, Y⁰m+j>0, то ця продукція не випускається X⁰_j=0, якщо Y⁰m+j=0, то випуск j-го виду продукції рентабельний і X⁰_j>0, (j=1,…,n)...

З огляду на вищесказане і відповідність перемінних, знайдемо оптимальний план двоїстої задачі за даними симплекса-таблиці з оптимальним планом.

Одержимо =(0;0;4,6;0;43,2;36;28,8)

З теореми 8 випливає, що min f = max Z = 36800.

З огляду на економічний зміст змінних двоїстих задач проведемо економічний аналіз результатів.

Рентабельний тільки випуск продукції першого виду (y⁰₄=0) у кількості X⁰₁=800од. Випуск інших видів продукції не рентабельний, при випуску один. продукції цих видів збитки складуть, відповідно, 43,2(У⁰₅), 36(У⁰₆), 28,8(У⁰₇) грош. одиниць. Тому X⁰₂=X⁰₃=X⁰₄=0. При такому плані випуску максимальна вартість випущеної продукції складе 36800 ден. од. При цьому верстатні ресурси цілком витратяться, їхній залишок X⁰₇=0, вони дефіцитні, їхня ціна за один. складе В⁰₃=4,6 ден. од. Трудові та матеріальні ресурси витрачаються не цілком, вони не дефіцитні. Тому їхня ціна за одиницю. У⁰₁=У⁰₂=0 і залишки, відповідно X⁰₅=600, і X⁰₆=3400од.

З огляду на вищевикладене, для збільшення сумарної вартості випущеної продукції необхідно збільшувати запаси дефіцитного ресурсу, верстатного.

З теореми 8

(61)

Тому збільшення запасу верстатного ресурсу b₃ на один. приведе до збільшення максимальної сумарної вартості випущеної продукції на В⁰₃ =4,6 грош. од.

3) досліджуємо допустимі границі зміни дефіцитного ресурсу, всередині яких змінні, вхідні в оптимальний базис, не змінюються, тобто не змінюється асортимент продукції, що випускається, а змінюється тільки її обсяг у залежності від чи збільшення зменшення ресурсу на ∆b. Якщо дефіцитним є i-ресурс, то з огляду на лінійність матричних перетворень, можна показати [1], що новий оптимальний план при зміні i-го ресурсу на ∆b_i буде

(62)

причому

(63)

З (62) і (63) знайдемо ∆b₃, m=4

Т оді b₃ + ∆b₃ буде змінюватися

8000-8000≤b₃≤8000+2000

0≤b₃≤10000

Таким чином, якщо ринок не насичений продукцією першого виду і маються конкуренти, підприємству доцільно зменшити запаси трудових і матеріальних ресурсів на 600 і 3400 од., відповідно, і за рахунок цих засобів закупити 2000ед.верстатних ресурсів. Це приведе до збільшення випуску продукції першого виду до X⁰₁ = 800+0,1*2000 = 1000 од. і вартості випущеної продукції до 46*1000 = 46000 ден. од., тобто на 4,6*2000 = 9200 грош. од.

Якщо на ринку немає конкурентів з реалізації продукції першого виду, тобто підприємство монополіст, то збільшення вартості продукції можна домогтися іншим шляхом, за рахунок збільшення її ціни. Досліджуємо допустимі межі її зміни ∆C .При цьому будемо використовувати оптимальне рішення двоїстої задачі В₀, що знаходиться в оцінному рядку останньої таблиці. Формули, аналогічні (62), (63) мають вид

(64)

причому

(65)

де - вектор – рядок останньої симплекс-таблиці, що відповідає виду продукції, що випускається.

У нашій таблиці це третій рядок. Тоді

∆З₁≥0 ∆З₁≥0

43.2+1.2∆З₁≥0 ∆З₁≥-36

36+∆З₁≥0 => ∆З₁≥-36 => ∆З₁≥0

28.8+0.8∆З₁≥0 ∆З₁≥-36

4.6+0.1∆З₁≥0 ∆З₁≥-46

Тоді 46≤C₁<∞

Одержали, що теоретично ціну на продукцію першого виду можна збільшувати необмежено.

4) проаналізуємо доцільність розширення асортименту за рахунок випуску продукції П-5. Для цього порахуємо для отриманих оптимальних цін на ресурси їхні сумарні витрати на єдиний.П-5. Одержимо 5·У⁰₁+6·У⁰₂+9·У⁰₃=5·0 + 6*0 + 9*4,6 = 41,4 грош. од. Тому що витрати менше планованої ціни один. продукції (41,4 < 50), то випуск продукції П-5 рентабельний і прибуток від випуску єдиний.П-5 складе 8,6 грош. од.