4. Симплексний метод рішення з.Л.П.

У попередньому розділі показано, що оптимальне рішення З.Л.П., якщо функція мети обмежена, досягається хоча б в одній з вершин багатогранника рішень і що кожній вершині відповідає опорний план З.Л.П., що задається системою m лінійно незалежних векторів із системи векторів Ā₁, Ā₂,…,Ā_n обмежень задачі. Тому оптимальний план рішення З.Л.П. можна знайти перебором усіх опорних планів (вершин) З.Л.П., яких не більше ніж число сполучень . При великих n і m велике і такий перебір недоцільний. Данциг запропонував процедуру цілеспрямованого перебору опорних планів зі зменшенням (збільшенням) функції мети. Таку процедуру він назвав симплексним методом, що дозволяє за кінцеве число кроків, починаючи з початкового опорного плану, одержати її оптимальний план. Якщо задача не має плану чи її функція мети не обмежена на багатограннику рішень, то симплексний метод дозволяє установити це у процесі рішення.

1. Вимоги до з.Л.П. Для можливості її рішення симплексом-методом.

З вищевикладеного випливає, що застосування симплекса-методу вимагає наявності початкового опорного плану З.Л.П. При канонічній формі зображення З.Л.П. з обмежень задачі легко одержати такий опорний план. Канонічна форма З.Л.П. задовольняє трьом вимогам:

1. обмеження – у виді рівностей;

2. праві частини b_i≥0

3. кожне обмеження містить базисну перемінну. Загальний вид З.Л.П. у канонічній формі

(22)

Тоді початковий опорний план: базисні перемінні X₁=bi , вільні перемінні

(23)

-план, тому що

X₁· ₁+X_{2 2}+....+X_{m m}= _o= (24)

План опорний, тому що вектори Ā₁,…,Ā_m із системи (22)

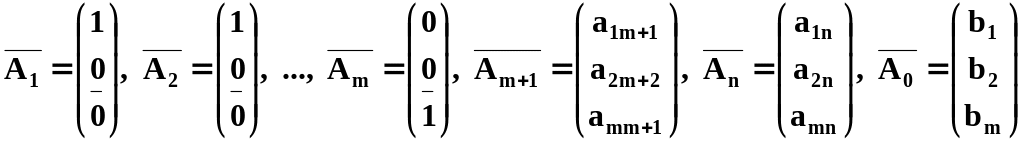(25)

одиничні, а, отже, лінійно незалежні, тобто базисні, і X₁, X₂,…X_mу розкладанні (24) ненегативні.

2. Побудова опорних планів.

Розглянемо, як, виходячи від початкового опорного плану (23) перейти до іншого опорного плану. Вектори Ā₁, Ā₂,…,Ā_m-базис у m-мірному просторі, тому будь-який вектор з (25) можна зобразити

(26)

Нехай Ā_m+1 не входить у базис і в його розкладанні

X_1m+1 Ā₁+X_2m+1 Ā₂ ,…,X_mm+1Ā_m=Ā_m+1 (27)

є хоча б один X_im+1>0

Візьмемо Θ>0, помножимо (27) на Θ і віднімемо цей добуток з (24). Одержимо

(X₁-ΘX_1m+1) Ā₁+(X₂-ΘX_2m+1)Ā₂+…+(X_m-ΘX_mm+1)Ā₂+ΘĀ_m+1=Ā₀ (28)

Переносячи ΘĀ_m+1 у ліву частину одержимо, що вектор

=(X₁-ΘX_1m+1,X₂-ΘX_2m+1,..,X_m-ΘX_mm+1,Θ,0,..,0) (29)

є планом, якщо його компоненти ≥0 , тому що Θ≥0, то для всіх компонентів з X_im+10 ця умова буде дотримуватися. Тому розглянемо дотримання цієї умови для компонентів з X_im+1>0, тобто

X_i -ΘX_im+1≥0 при X_im+1>0 (30)

З (30) випливає, що при

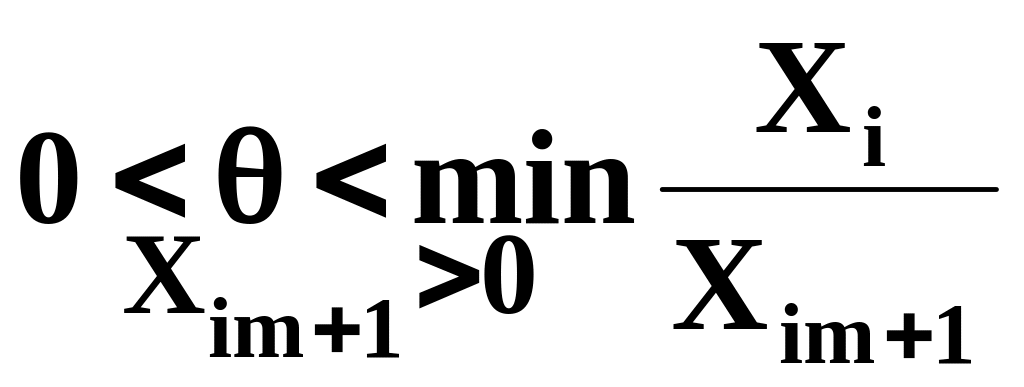(31)

умова незаперечності компонент нового плану буде дотримуватися. Щоб цей план став опорним, треба, щоб ≥0 компонент у стало m. А в (29) їх m+1. Тому необхідно принаймні один компонент зробити нулем. Це досягається за умови

(32)

У результаті план (29) стане опорним.

Виключення одного вектора з базису і включення замість нього іншого за допомогою Θ₀ відповідає переходу від одного базису до іншого за допомогою методу Жордана-Гаусса.

Таким чином, була отримана умова (32), що дозволяє визначати вектор (перемінну), виведену з базису при переході від одного опорного плану до іншого. Тепер треба одержати критерій для визначення вектора (змінної), що вводиться в базис, при цьому функція мети повинна убувати. Цей критерій є одним з основних елементів симплексного методу.

Зауваження 5.

Якщо вектор Ā_m+1 підлягає включенню в базис, а в його розкладанні (27) усі X_im+1≤0, то не можна вибрати Θ>0, яке б виключало один з векторів у розкладанні (28). У цьому

випадку план містить m+1 позитивний компонент, а система векторів Ā₁, Ā2,…,Ā_m+1 є лінейнозависиму (їх>m) і визначає не кутову, а внутрішню точку багатогранника рішень, у якій функція мети не може досягати мінімального значення.