Контрольные вопросы

1. Какова природа возникновения контактной разности потенциа­лов на границе металл-полупроводник?

2. Нарисуйте схему энергетических уровней в области контакта металл-полупроводник n- и p-типа при A_M > А_П и A_M < А_П без подачи внешнего напряжения.

3. Нарисуйте схему энергетических уровней в области контак­та металл-полупроводник n- или p-типа при подаче внешнего поля.

4. Получите выражение для тока через контакт металл-полупроводник согласно диодной теории.

5. Получите выражение для тока через контакт металл-полупроводник согласно диффузионной теории.

Список рекомендуемой литературы

1. Лысов В.Ф. Практикум по физике полупроводников. М.: Прос­вещение, 1976. 207с.

2. Шалимова К.В. Физика полупроводников. М.: Энергия, 1976. 416с.

3. Епифанов Г.И., Мома Ю.А. Твердотельная электроника. М.: Высш. шк., 1989. 383с.

4. Сугано Т., Икома Т., Такэиси Ё. Введение в микроэлектро­нику. М.: Мир, 1988. 320с.

5. Бонч-Бруевич В.Л., Калашников С.Г. Физика полупроводников. М.: Наука, 1977. 672с.

6. Росадо Л. Физическая электроника и микроэлектроника. М.: Высш. шк., 1991. 351с.

Лабораторная работа 2 изучение выпрямляющего действия электронно-дырочного перехода

ПРИБОРЫ И ПРИНАДЛЕЖНОСТИ: планшет с термостатом, германиевый и кремниевый диоды, схема питания, мультиметры типа CI-112 и CI-107.

ЦЕЛЬ РАБОТЫ: исследование вольт-амперной характеристики плос­костного диода и ее зависимости от температуры, определение ширины запрещенной зоны материала полупроводниковых диодов.

ТЕОРИЯ

Обычно электронно-дырочный переход создают внутри полупровод­ника путем введения в одну его часть акцепторной примеси, а в дру­гую – донорной. Тогда одна область имеет дырочную проводимость, а другая – электронную. Переход между двумя областями полупроводника называется электронно-дырочным (p-n или n-p). Переход, линейные размеры которого, определяющие его площадь, значительно больше его толщины называют плоскостным. Переход называют симметричным, если концентрация акцепторов в дырочной области ( ) равна кон­центрации доноров в электронной области ( ) и несимметричными, если концентрации примесей и неодинаковы. Переход, в котором область изменения концентрации примеси значительно меньше области пространственного заряда, называют резким. Переход, в котором тол­щина области плавного изменения концентрации примеси сравнима с толщиной области пространственного заряда, называют плавным.

Благодаря тому, что в рассматриваемой p-n-структуре концент­рация дырок в p-области выше, чем в n-области (p_p > p_n), а концент­рация электронов в p-области выше, чем в p-области ( ), на границе электронной и дырочной областей существует градиент концентрации носителей заряда, вызывающий диффузионный ток: дырок из p-области в n-область и электронов из n-области в p-область. Диффузионный перенос заряженных частиц сопровождается нарушением электрической нейтральности полупроводника в непосредственной бли­зости от границы областей: в p-области вследствие ухода дырок воз­никает нескомпенсированный отрицательный заряд, а в n-области вследствие ухода электронов – положительный заряд. В результате ды­рочная область приобретает отрицательный потенциал относительно электронной области и в переходном слое создается электрическое по­ле, вызывающее дрейфовый ток.

При отсутствии внешнего электрического поля результирующий ток в полупроводнике должен быть равен нулю. Следовательно, диффузион­ный ток в переходе, вызываемый градиентом концентрации носителей заряда, должен уравновешиваться встречным дрейфовым потоком, обус­ловленным напряженностью собственного электрического поля в пере­ходе

. (1)

Таким образом, в p-n-переходе всегда существует градиент концентрации носителей заряда, вызывающий диффузию дырок и элект­ронов, и обусловленный им градиент потенциала собственного элект­рического поля – вызывающий встречные дрейфовые токи, уравновешивающие диффузионные токи:

, . (2)

Наличие этих градиентов концентрации носителей заряда в p-n-переходе обусловливает сущест­венное различие в электрических свойствах p-n-перехода и прилагающих к не­му p- и n-областей.

На рис. 1 приведены графики зависимостей концентрации примесей (рис. 1, а), носителей заряда (рис. 1, б), плотности заряда (рис. 1, в) и потенциала (рис. 1, г) для резкого p-n-перехода при условии, что . Из ри­сунка видно, что толщина переходного слоя, в котором имеется нес­компенсированный объемный заряд со стороны p-области ( ) больше толщины переходного слоя со стороны n-области ( ). Величины , , , связаны соотношением

. (3)

Общая толщина p-n-перехода , как следует из (3), равна

. (4)

Контактная разность потенциалов , складывающаяся из потен­циалов и n- и p-областей, определяется следующим выражением

. (5)

На рис. 2, а приведена энергетическая диаграмма уединенных p- и n-областей полупроводника. В p-области уровень Ферми смещен

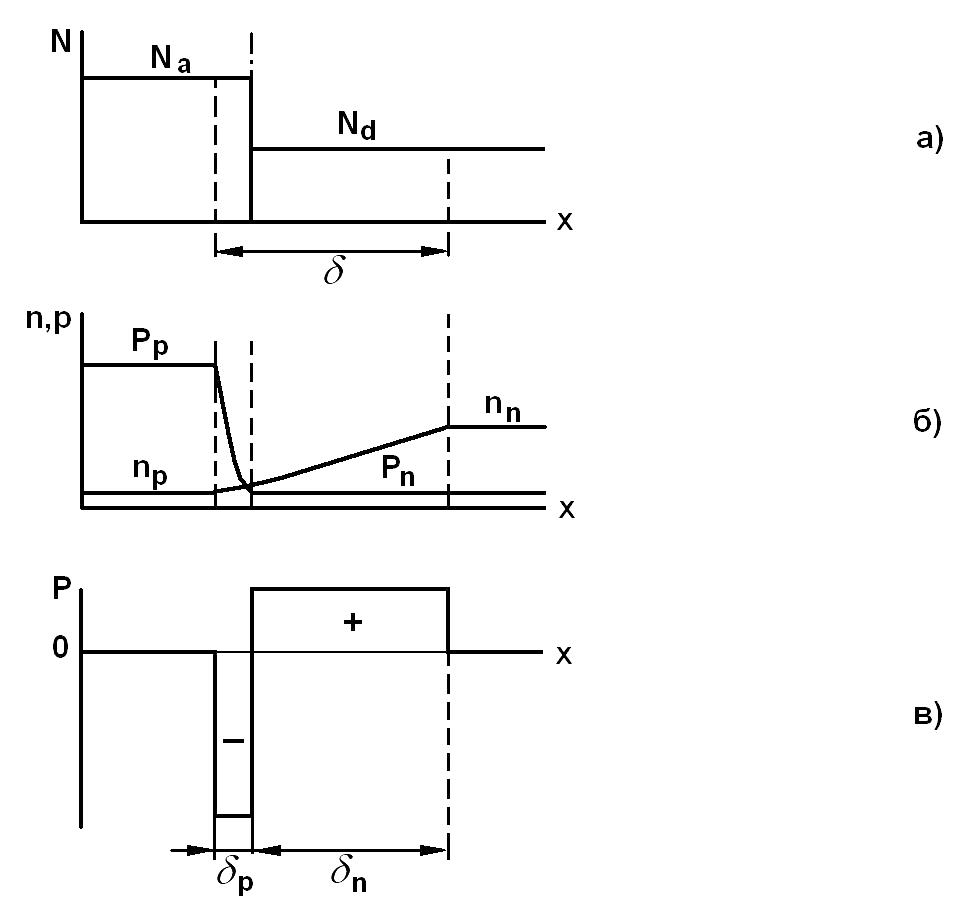
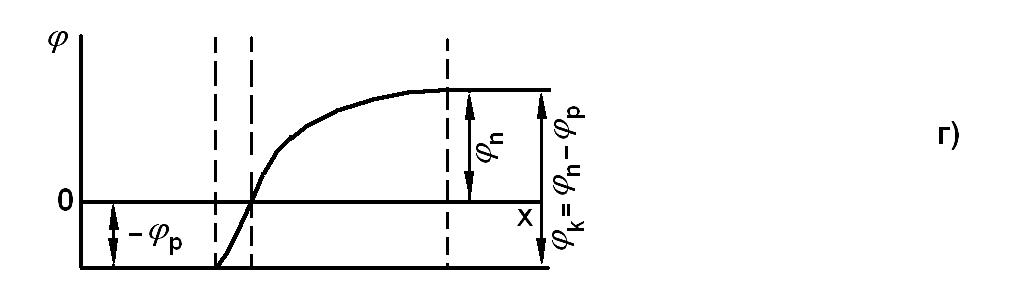
Рис. 1

в сторону валентной зо­ны, а в n-области уровень Ферми смещен в сторону зоны проводи­мости.

На рис. 2, б приведена энергетическая диаграмма p-n-структуры, в

которой энергия уровня Ферми всюду одинакова, так как в любой

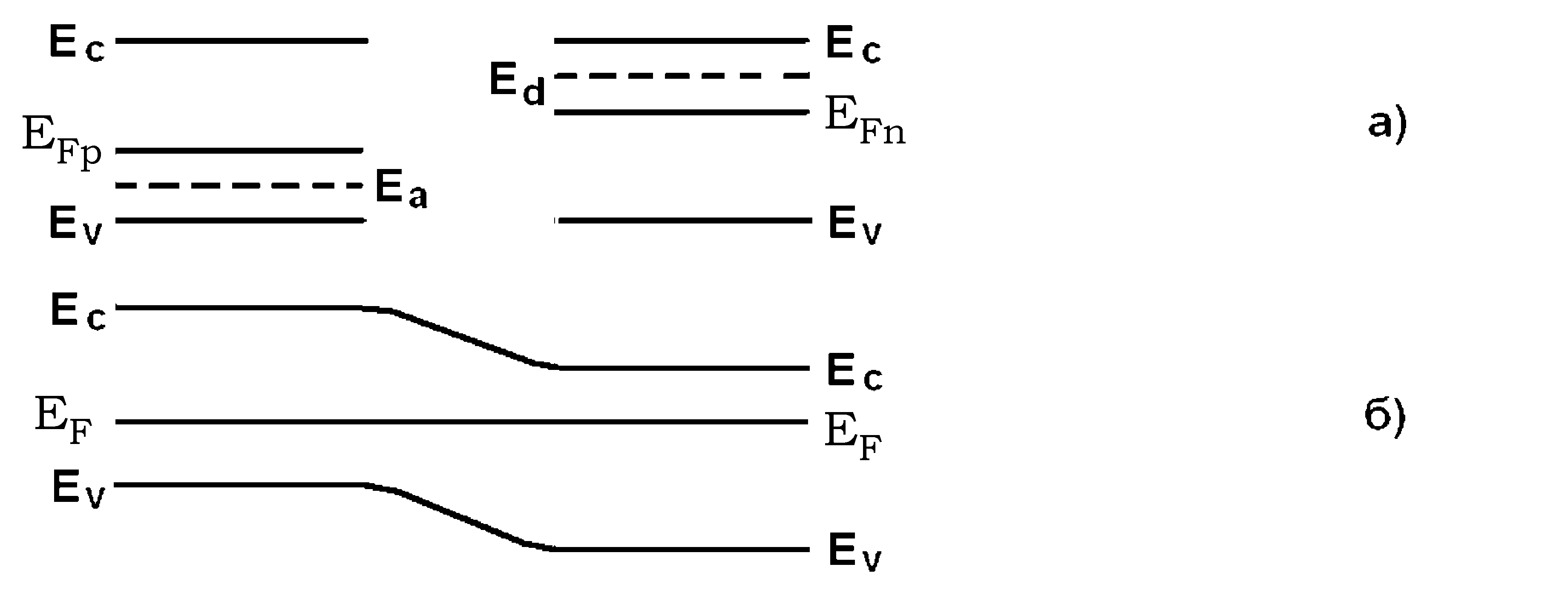
Рис. 2

точке тела уровень Ферми имеет одну и ту же вероятность заполнения его электронами , а одной и той же вероятности заполнения уровней должна соответствовать одна и та же энергия.

Поскольку расположение энергетических зон относительно уров­ня Ферми в каждой из областей фиксировано, из постоянства энергии уровня Ферми по всей структуре следует, что валентные зоны, а так­же и зоны проводимости p- и n-областей, должны быть смещены от­носительно друг друга на величину .

Из условий динамического равновесия процессов диффузии и дрейфа носителей заряда в p-n-переходе следует, что

. (6)

Непосредственно в области перехода энергетические уровни как в зоне проводимости, так и в валентной зоне расположены наклонно, что свидетельствует о наличии градиента потенциала, а следовательно, и электрического поля, которое выталкивает подвижные носители заряда из перехода. По этой причине концентрация электронов и ды­рок в переходе очень низка.

Рассмотрим прохождение тока через p-n-переход при наложе­нии внешнего электрического поля.

Прямой ток. Пусть внешнее напряжение приложено плюсом к p-области, а минусом к n-области. Концентрация подвижных носителей заряда внутри электронно–дырочного перехода значительно ниже, чем в p- и n-областях, поэтому сопротивление p-n-перехода значительно выше сопротивления p- и n-областей полупро­водника и падением напряжения в p- и n-областях полупроводни­ка можно пренебречь, приняв, что приложенное к полупроводнику напряжение полностью падает на переходе. Напряжение на пере­ходе в этом случае уменьшается и становится равным

. (7)

Распределение потенциала показано на рис. 3, а и 3, б. Поскольку внешнее поле направлено навстречу полю перехода, ре­зультирующее поле в

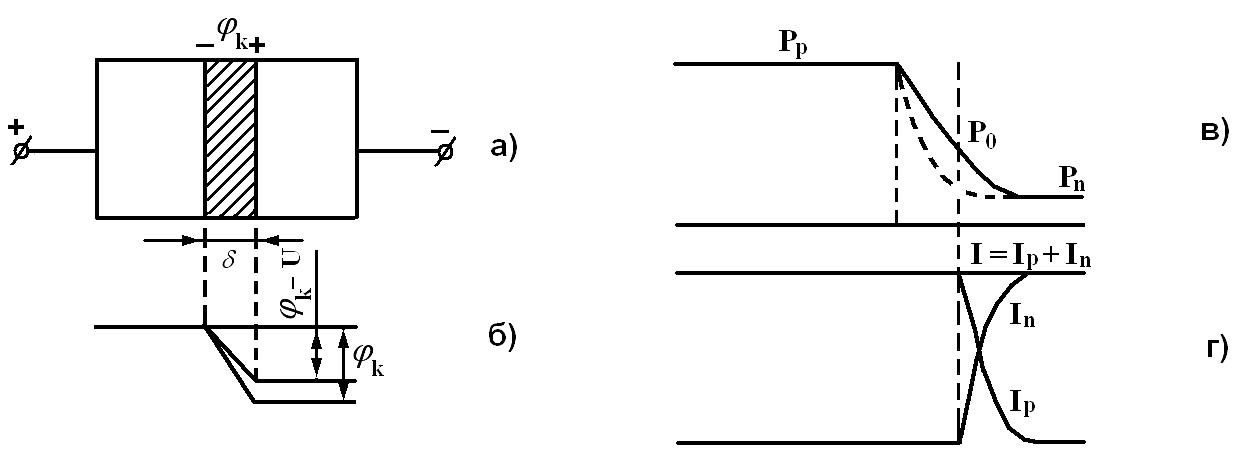
Рис. 3

переходе уменьшается. Вследствие этого нару­шается равновесие между дрейфовым и диффузионными токами, имевшее­ся при отсутствии внешнего напряжения. Дрейфовый ток становится меньше диффузионного, и результирующий ток через переход оказывает­ся не равным нулю:

. (8)

Ток, протекавший через переход, в данном случае называют прямым, а напряжение, приложенное к переходу, – прямым напряжением.

Тол­щину перехода, находящегося под прямым напряжением, можно опреде­лить из соотношения

. (9)

Отсюда видно, что при подаче прямого напряжения толщина перехода уменьшается. При этом уменьшается и сопротивление перехода, кото­рое, следовательно, является нелинейным.

Диффузия дырок через p-n-переход приводит к увеличению концентрации дырок на границе перехода (рис. 3, в). Возникающий при этом градиент концентрации дырок обусловливает дальнейшее диффу­зионное проникновение их вглубь n-области полупроводника, где дырки являются неосновными носителями заряда. Это явление назы­вают инжекцией носителей заряда. По мере диффузионного проникно­вения вглубь полупроводника инжектированные дырки рекомбинируют с электронами. В результате диффузионный ток за переходом постепенно спадает до нуля (рис. 3, г).

Инжекция дырок, однако, не нарушает электрической нейтраль­ности n-области, так как она сопровождается одновременным поступлением в n-область из внешней цепи точно такого же количества электронов. Результирующий ток, слагающийся из тока дырок и электронов, остается всюду постоянный (рис. 3, г) .

Одновременно с инжекцией дырок в n-область происходит инжекция электронов в p-область. Протекающие при этом процессы ана­логичны.

Прямой ток может достичь больших значений уже при небольших напряжениях.

Обратный ток. Если внешнее напряжение приложено плюсом к n-области, а минусом к p-области, то оно совпадает по знаку с контактной разностью потенциалов (рис. 4, а). Напряжение на пере­ходе в этом случае возрастает и становится равным

. (10)

Распределение потенциала в полупроводнике представлено на рис. 4, б.

Собственное поле перехода и внешнее поле, приложенное к пере­ходу, складываются, поэтому результирующая напряженность поля в переходе будет выше, чем при отсутствии внешнего поля. Это приво­дит к уменьшению диффузионного тока и преобладанию дрейфового тока. Результирующий ток через переход оказывается отличным от нуля:

. (11)

Направление этого тока противоположно направлению прямого тока, поэтому

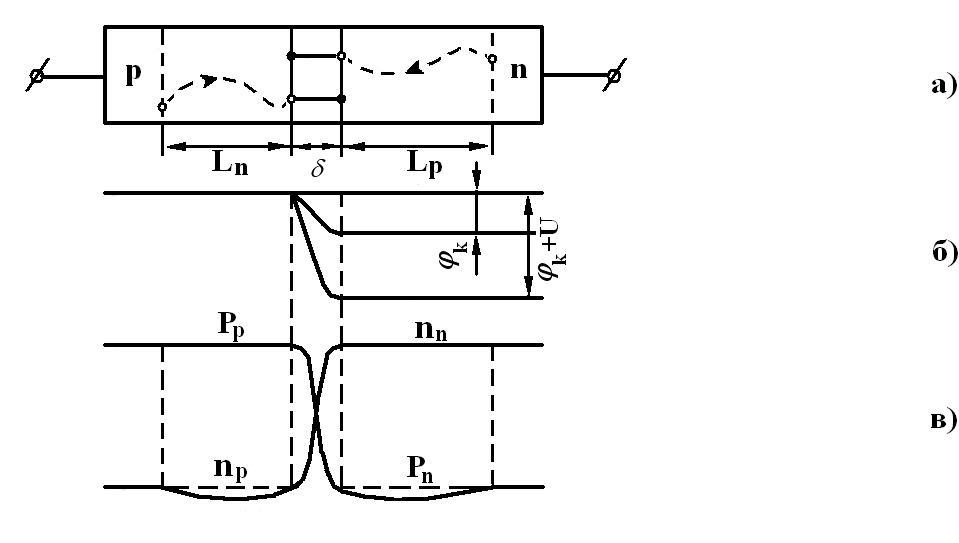
Рис. 4

его называют обратным током, а напряжение, вызывающее об­ратный ток – обратным напряжением.

Поле в переходе является ускоряющим лишь для неосновных носи­телей заряда, то есть для дырок n-области и для электронов p-об­ласти. В результате действия этого поля снижается концентрация но­сителей заряда за переходом (рис. 4, в). Поэтому возникает диффузия неосновных носителей заряда к границе перехода, где они подхваты­ваются полем и переносятся через переход. Это явление называется экстракцией носителей заряда.

Максимальное значение тока экстракции определяется, очевидно, числом неосновных носителей заряда, возникающих в полупроводнике в единицу времени на таком расстоянии от перехода, которое они смогут пройти за время жизни. Это расстояние для электронов или для дырок называют диффузионной длиной (рис. 4, а). Ввиду того, что число неосновных носителей заряда относительно невелико, ток экстракции через пере­ход (обратный ток) намного меньше прямого тока. От приложенного напряжения он практически не зависит и является в этом смысле током насыщения.

Таким образом, электронно-дырочный переход обладает нелиней­ной проводимостью: в прямом направлении проводимость перехода зна­чительно больше, чем в обратном.

Ток, проходящий через электронно-дырочный переход, равен

, (12)

где

, (13)

и – коэффициенты диффузии дырок и электронов, соответствен­но; концентрация дырок в n-области и концентрация электронов в p-области.

Вольт-амперная характеристика, соответствующая выражению (12), приведена на рис. 5.

При комнатной температуре величина примерно рав­на ,

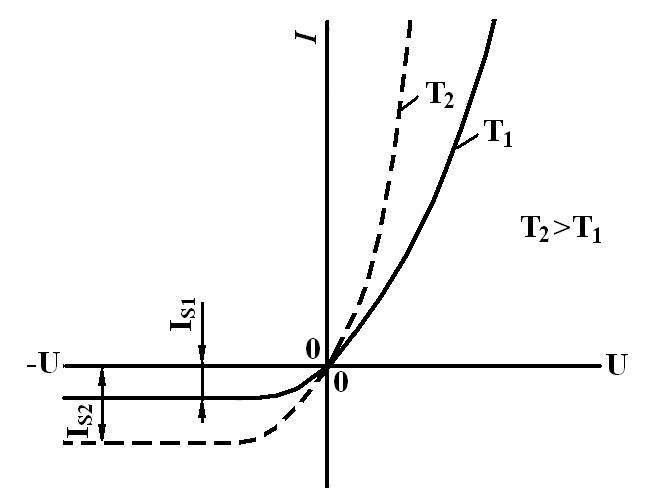
Рис. 5

поэтому уже при относительно небольшом прямом напряжении (порядка десятка милливольт) ток через переход резко возрастает приблизительно по экспоненциальному закону. При подаче обратного напряжения ток, изменив направление, быстро достигает значения , а далее остается постоянным независимо от величины напря­жения .

На вольт-амперную характеристику диода оказывает существен­ное влияние температура окружающей среды: при повышении темпера­туры резко возрастает обратный ток перехода , становится более крутой прямая ветвь характеристики.

Причина этих явлений заключается в сильной зависимости кон­центрации неосновных носителей заряда от температуры. Так, в электронном полупроводнике концентрация дырок с повышением температуры возрастает по экспоненциальному закону:

, (14)

где ширина запрещенной зоны полупроводника.

Для концентрации дырок в n-полупроводнике записывается аналогичное выражение. После подстановки их в уравнение (13) имеем

, (15)

или

, (16)

где

. (17)

На величину температура практически не влияет, следовате­льно, ток экстракции с повышением температуры увеличивается по экспоненциальному закону.

Зависимость прямого тока от температуры определяется следую­щим соотношением, вытекающим из выражений (12) и (16):

. (18)

В рабочем режиме , поэтому показатель экспоненты от­рицателен и с повышением температуры прямой ток возрастает.