Министерство образования Российской Федерации

Челябинский государственный университет

В.М. Чернов

ЛАБОРАТОРНЫЙ ПРАКТИКУМ ПО ФИЗИКЕ ТВЕРДОГО ТЕЛА И ТВЕРДОТЕЛЬНОЙ ЭЛЕКТРОНИКЕ

Учебное пособие

Челябинск 2004

В.М. Чернов

Лабораторный практикум по физике твердого тела и твердотельной электронике: Учебное пособие / Челяб. гос. ун-т. Челябинск, 2004, 84 с.

Учебное пособие содержит описания лабораторных работ по курсу “Физика твердого тела и твердотельная электроника”.

Предназначено для студентов 4-го курса физического факультета, обучающихся по специальности “Радиофизика и электронака”.

Ил.32. Библиогр.: 13 назв.

Печатается по решению редакционно-издательского совета Челябинского государственного университета.

Рецензенты: кафедра технологии приборостроения Южно-Уральского государственного университета;

доктор технических наук, профессор В.В. Родионов

«Челябинскиий государственный

Университет», 2004

Введение

Данное учебное пособие содержит описания лабораторных работ по курсу “Физика твердого тела и твердотельная электроника”: Контактные явления на границе раздела между полупроводником и металлом, Изучение выпрямляющего действия электронно-дырочного перехода, Изучение температурной зависимости характеристик биполярного транзистора, Исследование емкостных свойств полупровдниковых диодов, Туннельный эффект в p-n-переходе вырожденных полупроводников, Изучение фотопроводимости полупровдников, Фотоэлектрические свойства электронно-дырочного перехода.

Лабораторная работа 1 контактные явления на границе раздела между полупроводником и металлом

ПРИБОРЫ И ПРИНАДЛЕЖНОСТИ: планшет, термостат, диод с контактом Шоттки, блок питания, мультиметры типа C1-107 и C1-112, электронная схема для съемки вольт-амперных характеристик диодов.

ЦЕЛЬ РАБОТЫ: исследование распределения потенциалов в зоне контакта по­лупроводника и металла, снятие вольт-амперной характеристики диода с барье­ром Шоттки при различных температурах, определение контактной разности потенциалов между по­лупроводником и металлом.

ТЕОРИЯ

При исследовании электрических свойств полупроводников и в производстве полупроводниковых приборов обычно приходится обеспе­чивать электрический контакт с ними с помощью металлических элект­родов. Различают два типа контактов металл-полупроводник: контакт Шоттки и омический контакт. Вольт-амперная характеристика контакта Шоттки имеет вып­рямляющий вид, то есть при одной полярности приложенного напряжения через структуру протекает электрический ток, а при другой – почти нет. При омическом контакте ток пропорционален приложенному напряжению любой полярности. Наличие контакта того или иного типа определяется соотношением работ выхода из металла и полупроводника и поверхностными состояниями.

Рассмотрим явления в контакте металл-полупроводник при отсутствии поверхностных состояний. Примем, что полупроводник находится в области истощения донорной или акцепторной примеси (доноры и акцепторы полностью ионизованы, то есть отдали все свои электроны и дырки в зону проводимости и валентную зону, соответственно). Возьмем контакт электронного полупроводника и металла и предположим, что работа выхода электрона из полупроводника меньше работы выхода электрона из металла (рис. 1, а).

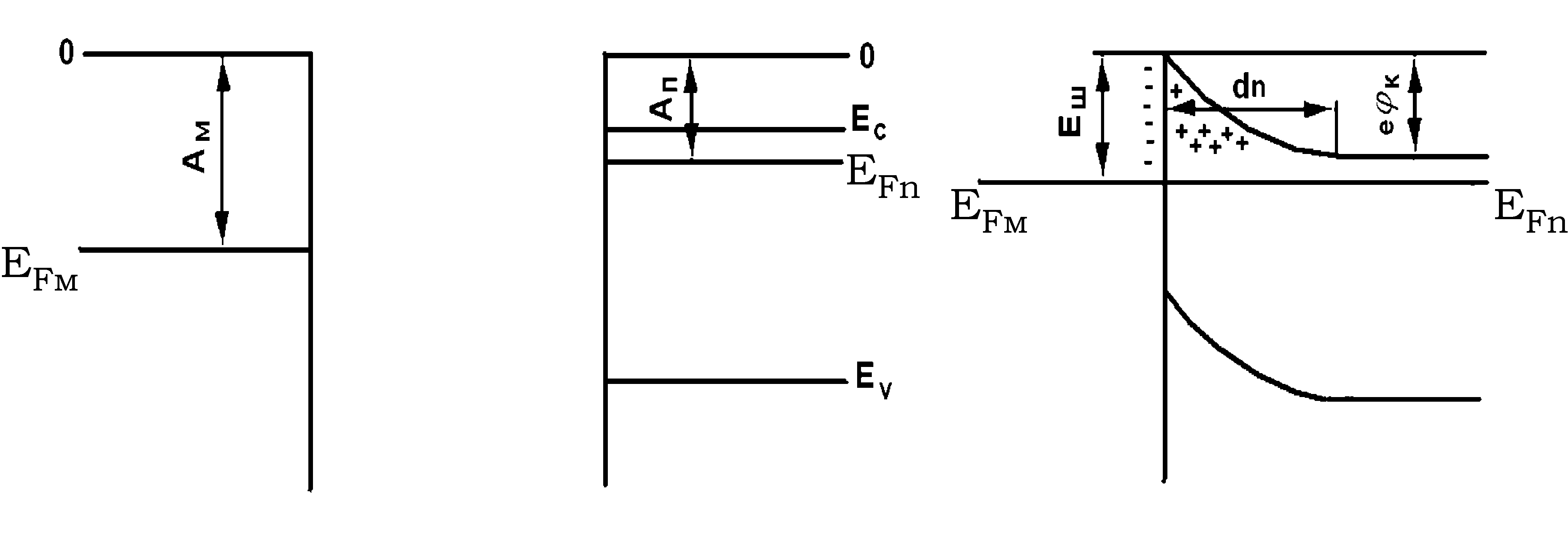
металл полупроводник металл полупроводник

a б

Рис. 1

Если металл и полупроводник привести в непосредственный кон­такт, то электроны будут переходить преимущественно из полупровод­ника в металл, так как уровень Ферми в полупроводнике перед соеди­нением с металлом расположен выше, чем в металле. При этом металл будет приобретать отрицательный потенциал, а полупроводник – положительный. Направлен­ный поток электронов будет иметь место до тех пор, пока уровни Ферми не выравняются и не установится динамическое равно­весие (рис. 1, б). После наступления этого равновесия между металлом и полупроводником возникнет кон­тактная разность потенциалов:

. (1)

Контактная разность потенциалов между металлом и полупроводником имеет значение порядка нескольких десятых долей или единиц вольта.

В приконтактных областях металла и полупроводника образуются области объемных зарядов. Из-за большой концентрации электронов в металле область объёмного заряда в нем очень тонка. Поэтому в этой области падение напряже­ния невелико и практически вся контактная разность потенциалов падает на области объемного заряда в полупроводнике и искривляет в нем зоны энергии. Если полупроводник n-типа и , то зоны энергии искривлены в приконтактной области кверху (рис. 1, б).

В области объемного заряда со стороны полупроводника существует электрическое поле, которое изгоняет оттуда свободные носители заряда. В результате, положительный объемный заряд оказывается обусловленным неподвижными носителями заряда – ионами доноров. Так как эта область практически лишена подвижных носителей заряда, она обладает повышенным сопротивлением по сравнению с пассивной частью полупроводника и называется обедненным слоем. Толщина области объемного заряда (обедненного слоя) d_n определяется соотношением

, (2)

где – концентрация носителей заряда.

Если работа выхода электрона из полупроводника -типа боль­ше работы выхода из металла, то электроны переходят из металла в полупроводник и образуют в его контактном слое отрицательный объем­ный заряд (рис. 2, а). При этом на поверхности металла возникает положительный заряд. Между металлом и полупроводником возникает контактная разность

по­тенциалов и потенциальный барьер . Образующееся контактное по­ле проникает вглубь полупроводника и уменьшает энергию электронов, вследствие чего происходит искривление энергетических уровней

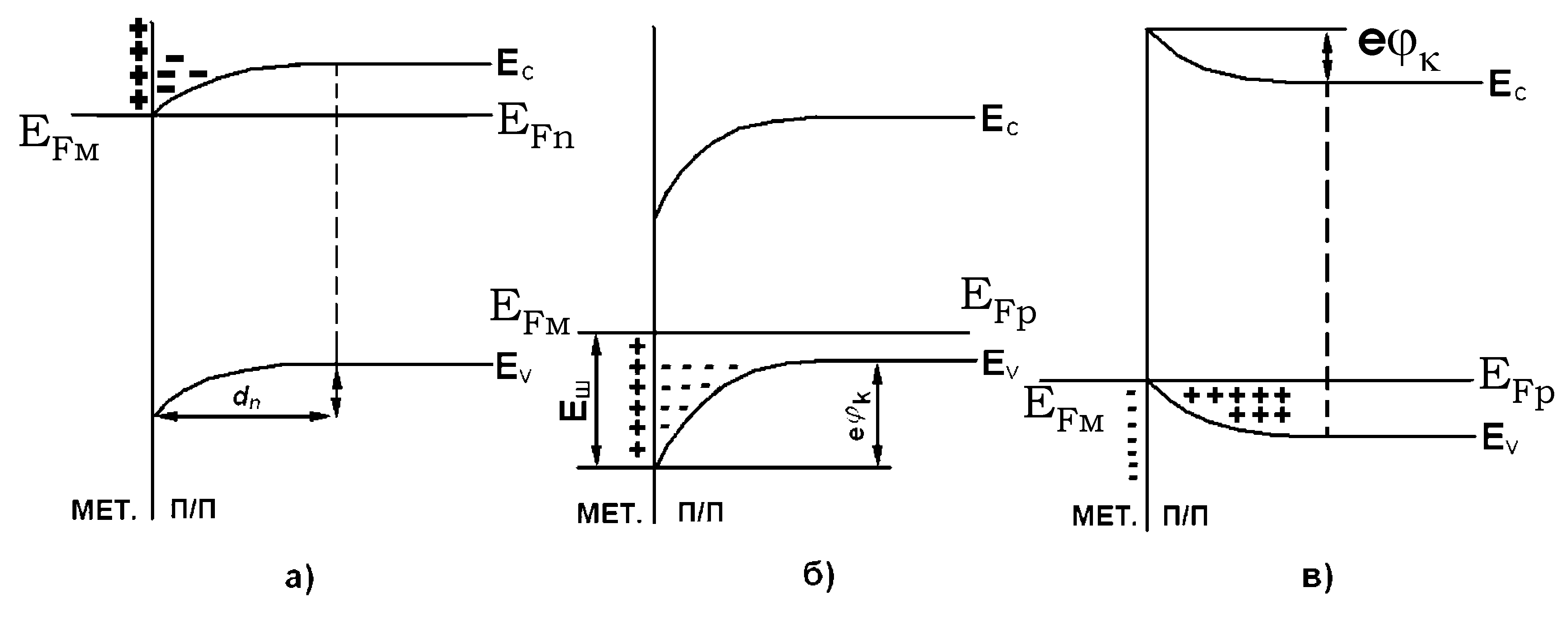
Рис. 2

полупроводника книзу. В этом случае область объемного заряда в полупро­воднике толщиной оказывается обогащенной свободными носителями

заряда и обладающей благодаря этому пониженным сопротивлением по сравнению с пассивной частью полупроводника.

При контакте металла с полупроводником -типа, когда работа выхода электронов из металла меньше работы выхода из полупровод­ника , в полупроводнике образуется обедненный слой (рис. 2, б). Когда же , в полупроводнике образуется обогащенный слой объемно­го заряда (рис. 2, в). Слой, обогащенный основными носителями заряда, называется антизапирающим, а слой, обедненный основными носителями заряда, называется запирающим (блокирующим, выпрямляющим). Контакт металл-полупроводник, содер­жащий запирающий слой, является выпрямляющим и представляет собой контакт Шоттки.

Потенциальный барьер со стороны металла в области контакта Шоттки называется барьером Шоттки. Величина этого барьера кроме названной причины определяется еще наличием поверхностных состояний: дефектов в полупровод­нике на границе раздела, приводящих к смещению уровня Ферми, и пос­торонних плохо проводящих слоев (пленки, оксиды и т.д.) между ме­таллом и полупроводником.

Рассмотрим теперь изменение потенциального барьера на выпрямляющем контакте металл-полупроводник -типа, к которому приложено внешнее напряжение (смещение) (рис. 3).

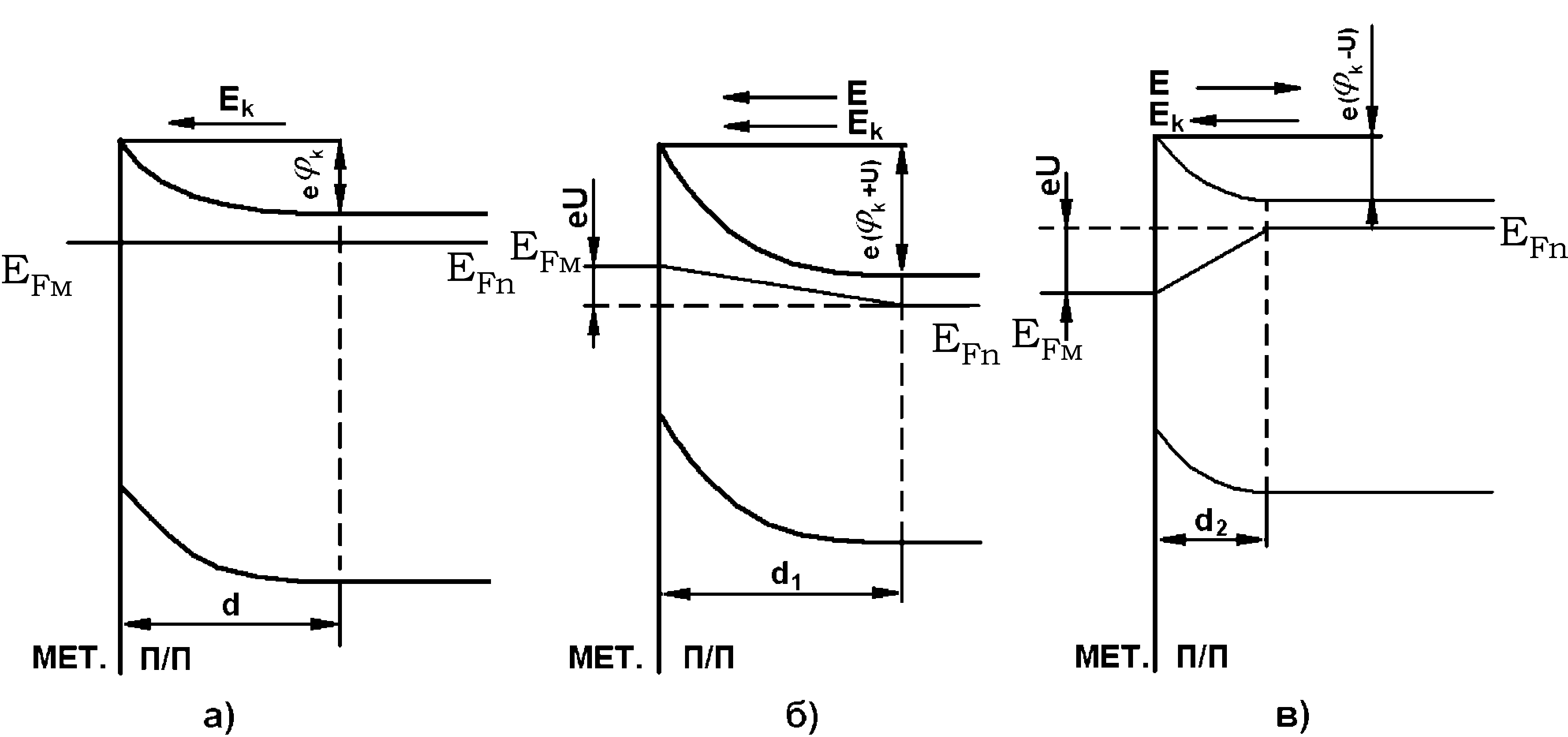
Рис. 3

Если к выпрямляющему контакту (рис. 3, б) электронного полупро­водника с металлом приложить внешнее напряжение в направлении, совпадающем с контактной разностью потенциалов (плюс источника по­дан на полупроводник), то потенциальный барьер со стороны полупро­водника увеличится на величину , а энергетические уровни электронов и уровень Ферми в полупроводнике сместятся на величину . Тол­щина запирающего слоя при этом увеличится и будет равна

, (3)

где – концентрация носителей заряда в полупроводнике. , если все доноры ионизованы (истощение примеси), а концентрация собственных носителей мала. Высота потенциального барьера со стороны металла – барьера Шоттки при этом не изменится. Такое направление называется запорным.

Если к выпрямляющему контакту приложить внешнее напряжение в направлении, противоположном контактной разности потенциалов (ми­нус источника подан на полупроводник), то потенциальный барьер со стороны полупроводника уменьшится на величину , а энергетичес­кие уровни электронов и уровень Ферми в полупроводнике сместятся на величину (рис. 3, в). Толщина запирающего слоя при этом умень­шится и будет

. (4)

Высота же барьера Шоттки останется неизменной. Такое направле­ние называют прямым. Сопротивление выпрямляющего контакта велико, поэтому практически все приложенное напряжение падает в слое объем­ного заряда толщиной или .

Для решения задачи о величине тока, проходящего через потен­циальный барьер контакта металл-полупроводник, существует две тео­рии. Применение той или иной теории связано с соотношением между толщиной барьера и длиной свободного пробега носителей заряда . Если сравнима с , то при прохождении барьера столкновениями но­сителей заряда с решеткой можно пренебречь. В этой случае задача о вычислении тока сводится к задаче о вычислении тока термоэлектрон­ной эмиссии с поверхности металла в полупроводник и обратно из по­лупроводника в металл с учетом приложенного внешнего напряжения. Расчет тока проводится так же, как и для вакуумного диода, только работу выхода следует заменить на высоту потенциального барьера и учесть обратный термоток из металла в полупроводник. Эта теория получила название диодной теории выпрямления. Она справед­лива для полупроводников с высокой подвижностью ( , , ). Если же длина свободного пробега электрона или дырки значительно меньше толщины барьера и носители заряда при прохождении барьера испытывают многократные столкновения с решеткой, то для вычисления тока через потенциальный барьер применяют диффузионную теорию. Она справедлива для полупроводников с малой концентрацией носителей заряда и малой длиной свободного пробега (закись меди, селен).

Приведем результаты диодной теории для контакта металл-полу­проводник -типа. В состоянии термодинамического равновесия и в отсутствие внешнего напряжения для термотока из металла в полу­проводник и из полупроводника в металл имеем выражение (формула Дэшмена)

, (5)

где

, (6)

, (7)

– площадь контакта; – эффективная масса электрона; – пос­тоянная Больцмана; – постоянная Планка.

Если приложить внешнее поле к контакту металл-полупроводник, то величина потенциального барьера со стороны полупроводника изме­няется в зависимости от знака приложенного напряжения:

, (8)

где знак минус при соответствует прямому направлению внешнего поля, а знак плюс – запорному. При этом величина тока, обусловлен­ного эмиссией электронов из полупроводника в металл, будет

. (9)

Ток направлен от металла к полупроводнику. Так как величина барьера со стороны металла при этом не изменяется, то величина то­ка, обусловленного эмиссией электронов из металла в полупроводник, равна

. (10)

Ток направлен от полупроводника к металлу. Используя выражения (9) и (10), найдем величину результирующего тока :

, (11)

где

. (12)

Уравнение (11) представляет собой уравнение вольт-амперной характеристики контакта Шоттки. 3нак "+" при соответствует прямому (пропускному) направлению внешнего поля, а знак "–" – за­порному (обратному). Из формулы (11) видно, что при T=const и напряжении ток через контакт растет по экспоненте. При нап­ряжении ток сначала медленно возрастает (по абсолютному значению) и при достаточно большом значении |U| стремится к предельному значению, численно рав­ному току насыщения I_s.

Рассмотрим теперь диффузионную теорию. Наличие в области запирающего слоя пространственного заряда и внутреннего поля, а также неоднородного распределения носителей приводит к возникновению двух потоков носителей заряда: диффузионного, обусловленного градиентом концентрации и дрейфового, обусловленного внутренним электрическим полем. Результирующий электрический ток является суммой дрейфового тока:

, (13)

где – подвижность, – концентрация носителей за­ряда, – напряженность электрического поля, и диффузионного тока

, (14)

где – коэффициент диффузии носителей заряда, – градиент концентрации вдоль оси х, перпендикулярной поверхности контакта.

В состоянии равновесия при отсутствии внешнего поля дрейфовый ток равен диффузионному. Они направлены в противоположные сто­роны, поэтому результирующий ток есть

. (15)

Учитывая, что , а концентрация в приконтактной об­ласти изменяется по закону

, (16)

выражение (15) можно записать в виде

, (17)

откуда следует соотношение

, (18)

которое называют соотношением Эйнштейна.

Если к контакту металл-полупроводник приложена внешняя разно­сть потенциалов , то ток через контакт будет равен

. (19)

Решение уравнения (19) дает для тока через контакт следующее выражение:

, (20)

где

, (21)

– напряженность поля у границы.

Если к контакту приложено напряжение в прямом направлении, то дрейфовый ток уменьшается и разность диффузионного и дрейфового тока экспоненциально возрастает до тех пор пока . При экспонента переходит в прямую линию. Если к контакту приложено напряжение в запорном направлении, т.е. внешнее поле складывает­ся с контактным, то дрейфовый ток увеличивается и в предельном случае; когда он становится много больше диффузионного, ток через контакт будет

. (22)

Как в диодной, так и в диффузионной теории получается одинако­вое выражение для вольт-амперной характеристики выпрямляющего кон­такта металл-полупроводник. Однако существует следующие различия в токах насыщения: 1) ток насыщения (21) много меньше, чем (12); и 2) ток насыщения (12) не зависит от приложенного напряжения, в то время как в (21) он растет для запорного направления с ростом приложенного напряжения.

Диодная и диффузионная теория в равной мере применимы и к ды­рочному полупроводнику, если в нем на границе с металлом имеется запирающий слой. При этом в уравнениях вместо надо писать , а плюс заменить на минус . Пропускным направлением в этом случае будет такое, когда на -полупроводник подан плюс напряжения.

Ток через контакт в прямом направлении в несколько десятков или сотен раз больше тока в обратном направлении при одном и том же значении приложенного напряжения. Это свойство контакта исполь­зуется для изготовления точечных диодов, широко применяемых в ра­диотехнике.

Большинство точечных диодов, используемых для выпрямления вы­соких частот, состоят из кристалла германия или кремния -проводимости толщиной 0,1 – 0,6 и площадью 0,5 – 1,5 , припаянно­го к кристаллодержателю контактного электрода в виде тонкой про­волочки и стеклянного баллона. В результате формовки под проволоч­ным электродом образуется -переход.