6.7 Расчёт прочности балки в стадии эксплуатации
6.7.1 Проверка размеров бетонного сечения
Размеры
сечения проверяют из условия:
обеспечивающего прочность бетона стенки по сжатой полосе между наклонными трещинами.
Vsd = 0,334 МН, т.к. поперечное армирование пока неизвестно, принимают (в запас прочности) А = 0, тогда по формуле:
;
1
= 1;
При отсутствии нагрузок малой суммарной продолжительности по табл.1.19./5/ принимают b2 = 0,9, поэтому fck = 0,9·35 = 31,5МПа; fctd = 0,9·2,2 = 1,98 МПа;
По формуле b1 = 1 - fck = 1 – 0,01·31,5= 0,685;
Для сечения 0 – 0:
b = 0,27 м; h0 = 0,79 м;
Vrd = 0,3·1·0,685·31,5·0,27∙0,79 = 1,38 МН;
Условие выполняется Vrd > Vsd = 0,334МН
Для сечения 1 – 1:
b = 0,12 м; h0 = 0,79 м;
Vrd = 0,3·1·0,685·31,5·0,08·0,79 = 0,409 МН;
Условие выполняется Vrd > Vsd = 0,334МН.
6.7.2 Прочность нормальных сечений
Проверяют прочность для опасного сечения 2 – 2, расположенного на расстоянии 0,5L от опоры. Установившееся предварительное напряжение арматуры определяют с учетом коэффициента точности напряжения:
где
–
при механическом способе натяжении
арматуры принимается равным 0,1.
Т.к. Mct = fctm ∙ Wpl,b = 3,2·0,0465 = 0,1488 МНм; Mrp = Pm,t (L0p + an,t) = =1315,21·(0,32+ 0,49) = 1,065 МНм; и следовательно, Mct/ Mrp = 0,1488/1,065=0,14 < 0,25, принимаем sp = 0,1. Тогда sp = 1 – 0,1 = 0,9.
Определяют граничные значения относительной высоты сжатой зоны бетона. Тогда:
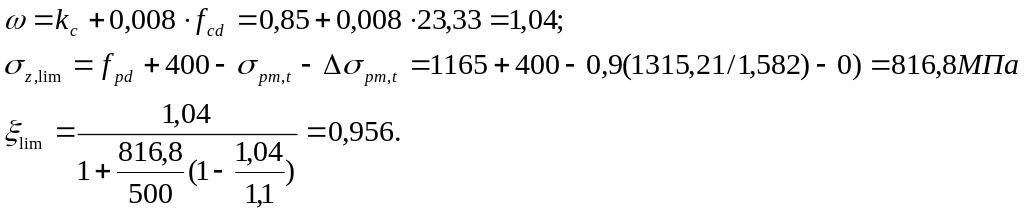Принимая
в первом приближении sn
= 1,15, проверяем условие:
fck b’f h’f + fyk A’s = 31,5·0,4·0,185 + 365·0,000314 = 2,446 МН < s6 fyk Asp = =1,15·1165·0,001532 = 2,05 МН. Так как оно не соблюдается, то граница сжатой зоны проходит в ребре и расчет выполняют как для элемента таврового сечения шириной
b’f = 0,4м, b=0,08м.
При sn = 1,15 высота сжатой зоны:
Поскольку
= x/h0
= 0,3/0,79 = 0,38 < lim
= 0,956, прочность проверяют из условия
при d0
= h
– a
= 0,79 – 0,1 = 0,69 м, тогда задаемся что
Несущая способность рассматриваемого сечения:
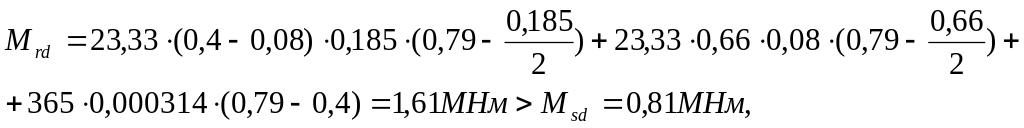
т.е. прочность сечения 2 – 2 обеспечена.
Прочность других нормальных сечений не проверяют, т.к. она тем более обеспечена.
6.7.3 Прочность наклонных сечений
Рассмотрим наклонное сечение, начало которого в растянутой зоне совпадает с наклонным сечением 1 – 1, т.е. с местом резкого изменения толщины стенки.
В этом месте толщина стенки равна 0,12м, но по мере удаления она уменьшается и становится равной 0,08 м, поэтому при расчете принимают (в запас прочности) b = 0,08 м.
Используя данные табл.7, определяют усилия обжатия в сечении 1 – 1 при sр = 0,9; Р0 = 0,9·797,33= 0,72 МН;
Тогда:
Принимаем
.
Проверяем условия:
где
= 0,25L
– Lx
= 0,25∙9,7 – 0,29 = 2,14 м.
Поскольку оба условия не выполняются, необходимо производить расчет поперечной арматуры.
Определяем
для опорного сечения. Поскольку
,
принимаем
,
тогда:
Подбираем
поперечную арматуру. Для наклонного
сечения от опоры до первого сосредоточенного
груза
=2,14
м; d
= 0,69м;
;
<
;
Принимаем
;
Поскольку:
<
то требуемая интенсивность поперечного армирования определяется по формуле:
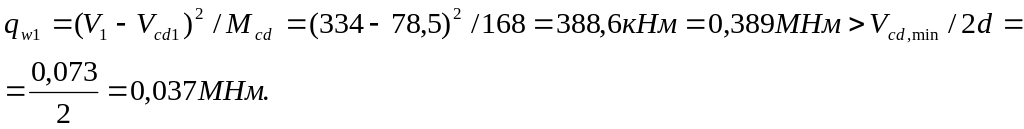
Наибольший шаг поперечных стержней определяем по формуле:
,
где V – значение поперечной силы на рассматриваемом участке
Принимаем
,
тогда требуемая площадь поперечных
стержней:
Принимаем 2 Ø10 S400 (As=1,57 см2) с шагом 100 мм.
Выясняем,
на каком расстоянии от опоры шаг
поперечных стержней может быть увеличен
от
до
.
При этом интенсивность поперечного
армирования:
;
;
.
Задаем
длину участка с шагом поперечных
стержней
равной расстоянию от опоры до первого
груза –
.
Проверяем условие
,
при значении
равным расстоянию от опоры до второго
груза
>
,
при этом
.
Значение
и
определяем по формуле:
;
<
;
<
Принимаем
.
Поскольку
>
,
;
>
Прочность этого наклонного сечения обеспечена.
Большое
значение
не рассматривается, поскольку при этом
поперечная сила резко уменьшается.
Таким
образом окончательно принимаем: на
приопорном участке длинной
шаг поперечных стержней
,
на следующем участке длинной
.
Выясняем
необходимость расчета прочности
наклонных сечений по изгибающему
моменту. Для этого по формуле
определяем момент образования трещин
в нормальном сечении, проходящем через
конец зоны передачи напряжений, т.е. на
расстоянии 0,99 м от торца балки.
Геометрические характеристики этого
сечения принимаем средними между
сечениями 1–1 и 2–2, т.е.
;
;
.
Полные потери предварительного
напряжения принимают такими же как
для сечения 2–2, т.е.
.
Момент от внешних нагрузок в рассматриваемом сечении:
;
усилие
предварительного напряжения
.
Момент образования трещин:
.
Поскольку трещины не образуются, прочность сечения по изгибающему моменту не рассчитывают.