Моделирование свойств (совокупности свойств) урбанизированной среды

Наиболее подходящей для математического описания любого -го свойства ( ) произвольного -го объекта ( ) обследуемой урбани­зированной территории является функция нормаль­ного закона распределе­ния на плоскости (закон Гаусса).

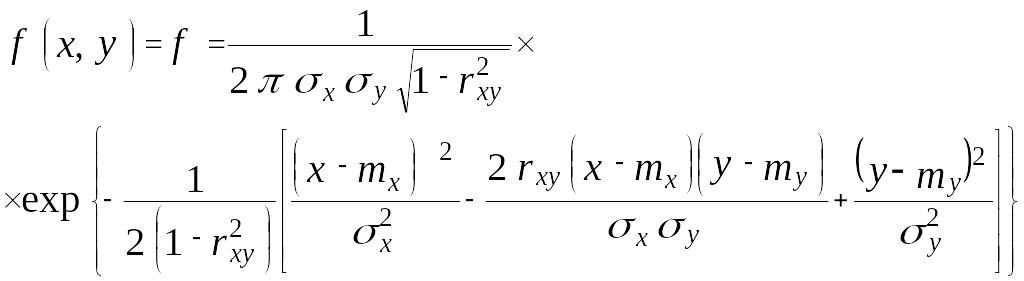(36)

где,

и - случайные величины;

- плотность распределения случай­ного вектора ( , ), то есть двухмерной случай­ной величины;

, - математические ожидания случайных величин и ;

, - средние квадратичные отклонения и ;

- коэффициент корреляции.

Применительно к модели некоторого j-го свойства любого объекта в (36) имеем:

и - координаты геодезической системы обследуемой террито­рии;

- функция плотности -го свойства -го объекта в геодезиче­ской системе координат;

, - координаты точки местонахождения -го объ­екта в системе координат ( , );

, - средние квадратические отклонения от точки местонахож­дения -го объекта, определяющие степень "затухания" влияния -го свой­ства -го объекта на окружающую ур­банизированную среду;

- коэффициент корреляции -го свойства -го объекта в координа­тах геодезической системы.

Таким образом, формулу (36) для математического представления j-го свойства -го объекта можно переписать в виде:

(37)

На практике чаще встречаются более простые случаи опи­сания -го свойства -го объекта:

- первый случай, ( и ), что соответствует некоррели­рованности (независимости) распространения -го свой­ства -го объекта относительно осей геодезической системы координат (рис. 2):

(38)

- второй, самый простой случай, ( ; ) соответст­вует круговому закону распределения Гаусса (рис. 3):

(39)

Рис.2. Геометрическая интерпретация математического описания

j-го свойства i-го объекта (общий случай).

Круговой закон Гаусса - самая удобная форма для практического описания -х свойств -х объектов урбанизированных терри­торий. Так как плотность двумерной случайной величины ( , ), то и функции -х свойств -х объектов можно также на­звать "плотностью" этих свойств. Вполне очевидно, что такое название полностью соответствует физиче­скому содержанию функции относительно рассматриваемых -х свойств -х объ­ектов.

Следует более подробно рассмотреть круговой закон Гаусса (39), так как возможные в практике оценки и обследования урбанизированных тер­риторий усложнения типа (38) и (37) логически с формальной очевид­но­стью выводятся из случая (39).

Рис.3. Геометрическая интерпретация кругового закона Гаусса

Функция плотности -го свойства -го объекта для об­щего случая (37) является функцией независимых переменных , (координаты произ­вольной точки в геодезической системе, в которой представлена обследуе­мая урбанизированная территория) и парамет­ров этого свойства:

, , , , , или:

(40)

Для кругового закона Гаусса (39) зависимость (40) упрощается:

(41)

где,

, - координаты местоположения рассматриваемого -го объ­екта в геодезической системе координат;

- среднеквадратическое отклонение от точки ( , ), оп­реде­ляющее степень "затухания" влияния -го свойства -го объекта на окру­жающую урбанизированную среду;

Вернемся к некоторым определениям, которые даны были ранее: "масса" -го свойства -го объекта, "степень затухания" -го свойства -го объекта, "функция плотности" (или "плотность") -го свойства -го объ­екта.

Пусть:

- "масса" -го свойства -го объекта, отражающая объем (полноту) этого свойства;

- "коэффициент затухания" влияния -го свойства -го объекта на окружающую среду;

- "функция плотности" ("плотность") -го свойства -го объ­екта.

Тогда для кругового закона Гаусса (39) имеем:

(42)

или с учетом ( 39 ):

(43)

где

- максимальная величина , то есть:

(44)

В отличие от теории вероятности, где

(45)

не равно единице, так как это вполне конкретная "масса" -го свойства -го объекта (объем, полнота), получаемая из исходных данных при анализе объектов и обследовании урбанизированных тер­риторий. То­гда и в виду линейной функции (43) пропорциональна и может быть вынесена за знаки интегралов:

(46)

Таким образом, "функция плотности" -го свойства -го объ­екта в от­личие от классического определения плотности вероятности случайных величин зависит от параметра - "массы" (объема, полноты) -го свой­ства, то есть:

(47)

что очень важно для решения задач по анализу объектов и обследова­нию урбанизированных территорий.

Таким образом, математической моделью -го свойства -го объ­екта (для кругового закона влияния этого свойства на окружающую среду - кру­говой закон Гаусса) является выражение (47). Эта модель, как видно из выражения (47) требует решения обратной задачи ( ) по выражению (46). Для ее решения можно использовать таб­лицы функций Лапласа, а саму задачу решать с помощью вычислительной техники.