2. Знакомство с установкой

На стенде представлена схема трехфазной линии электропередачи напряжением 35 кВ (рис.3) и ее однофазная действующая электрическая модель, выполненная с соблюдением масштабных коэффициентов подобия (рис.4). Номинальное напряжение модели - 100 В. Модель содержит следующие элементы:

1. автотрансформатор (Т), имитирующий источник питания;

2. линейные активное и индуктивное R_Л и Х_л сопротивления, имитирующие сопротивления линии электропередач;

3. нагрузочные активное и индуктивное R_H и Х_н сопротивления, имитирующие активно-индуктивную нагрузку, приведенную к концу линии;

4. набор конденсаторов различной емкости с выключателями, смонтированными на стенде;

5. выключатель SA1, предназначенный для одновременного выключения всех конденсаторов;

6. выключатели SA2 и SA3 - для переключения обмотки напряжений ваттметра в начало и конец схемы модели.

Стенд, кроме того, снабжен комплексом измерительных приборов: амперметром mА (для измерения силы тока в цепи), ваттметром W и вольтметрами V₁ и V₂ (для измерения активной мощности и напряжения в начале и конце линии), однофазным фазометром φ (для измерения cosφ). Питание на стенд подается через установленный в левом углу панели автоматический выключатель QF. Контроль наличия напряжения в схеме модели производится сиг­нальной лампой HL.

Условием полной компенсации реактивной индуктивной нагрузки модели является равенство

(14)

где Q_L - индуктивная нагрузка; Q_c - мощность конденсаторов.

Необходимую емкость для полной компенсации можно приближенно определить, зная режим работы линии до компенсации, т.е. зная U₂, Ih, cosφ_H.

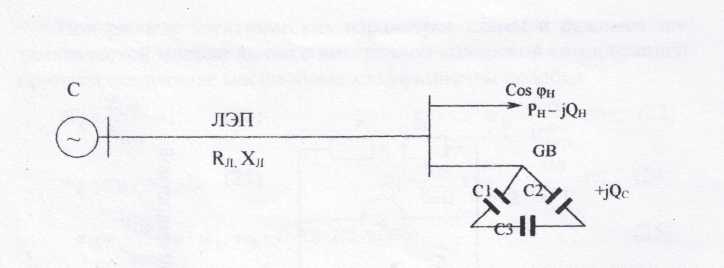
Рис. 3. Схема трехфазной ЛЭП с поперечной ёмкостной компенсацией

Полная и реактивная индуктивная мощность нагрузки составляют

S_H = U₂·I (15)

Q_L = S_H ·sinφ_H = U₂·I· sinφ_H (16)

Учитывая, что Q_L = Q_С, а Q_С = , записываем:

U₂·I· sinφ_H = (17)

Из последнего равенства получаем, что

(18)

Выражая ток в амперах, напряжение в вольтах, а емкость в микрофарадах, окончательно получаем зависимость для определения значения полной емкости для поперечной компенсации реактивной мощности модели линии:

(19)

где I - ток нагрузки при выключенной поперечной емкости, А; U₂ - напряжение в конце линии, В; φ_Н - угол сдвига по фазе между током и напряжением на нагрузке; ω - угловая частота.

При частоте f =50 Гц и ω = 2 · 3,14 · 50 = 314 формула (19) примет вид:

При расчете электрических параметров схемы и режимов математической модели линии с поперечной емкостной компенсацией приняты следующие масштабные коэффициенты подобия:

(21) (22)

(23) (24)

(25)

Номинальное напряжение модели линии .

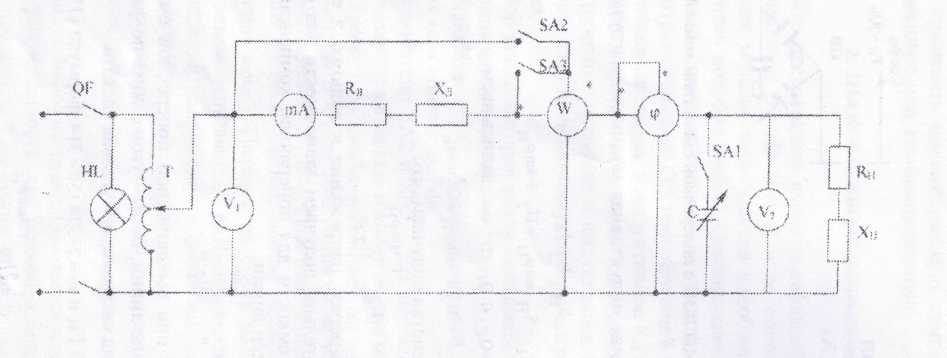
Рис,4. Схема однофазной модели переменного тока ЛЭП с поперечной емкостной

компенсацией