2.2.2. Основные погрешности измерения. Суммирование погрешностей

Деление основной погрешности измерений на систематическую и случайную очень важно, так как эти составляющие по-разному проявляются, и их оценивание требует разного подхода.

Применительно к CTD–измерениям систематическая компонента инструментальной погрешности эквивалентна точности определения градуровочной кривой, и, как правило, определяется одним значением, ∆_isХ = К_х.

Случайные погрешности, в отличие от систематических, подчиняются вероятностным законам.

Предположим, что CTD–зондирование выполнялось в слое морской воды, который однороден по параметру Х, а измеренная реализация Х(t) не содержит систематическую погрешность. В соответствии с аксиомой случайности, среднее значение функции x(t) отклонения величины параметра Х(t) от его среднеарифметического значения определённое на этом интервале Δt

(2.3)

должно равняться нулю. Дисперсия D (рассеяние):

. (2.4)

позволяет оценить среднеквадратическую погрешностью  результатов измерения.

Если эти результаты действительно содержат только случайные погрешности, то плотность распределения вероятностей значений X будет описываться нормальным законом распределения (уравнением закона Гаусса):

. (2.5)

На рис. 2.1 представлены два варианта нормального распределения значений случайной погрешности, р(ΔХ₁) и р(ΔХ₂). Измерения X₁, выполненные с меньшим разбросом значений , отличаются более острой формой вершины кривой распределения.

В практике измерений гидрологических параметров можно считать, что случайные погрешности подчинены нормальному закону (2.5). Поэтому для их оценки используется значение среднеквадратического отклонения результата измерения , установленного по дисперсии (2.4) профиля Х(t) на интервале измерения Δt, в пределах которого отмечается (либо предполагается) отсутствие стратификации морской среды по параметру Х.

При нормальном законе распределения случайной погрешности измерения параметра Х за максимальную погрешность принимается величина ∆_icХ  3_X:

. (2.6)

Случайные погрешности по значению превосходящие эту величину встречаются крайне редко (вероятность менее 0,3 %).

Кроме выражения (2.5), для нормального закона распределения приняты следующие соотношения между вероятностями и средними квадратическими отклонениями:

, (2.7)

. (2.8)

По корреляционной функции R(τ):

. (2.9)

определяется общая зависимость значений погрешности x(t) в некоторый момент времени t от значений в другой момент t+τ. Для количественной характеристики зависимости между случайными погрешностями x₁(t) и x₂(t+τ), взятыми через интервал τ, используют коэффициент корреляции:

. (2.10)

При тождественном равенстве x₁(t)≡x₂(t) и отсутствии смещения τ=0 коэффициент корреляции r(τ)=1.

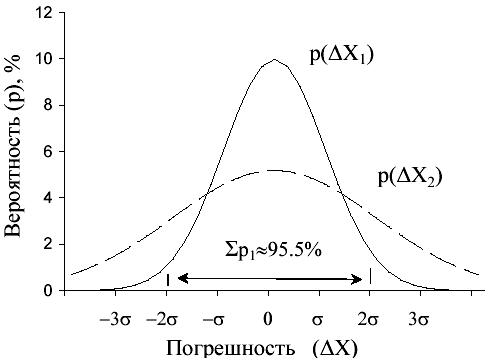
Рис. 2.1. Нормальное распределение значений случайной погрешности

При суммировании составляющих погрешности измерения необходимо исходить не из признака разделения погрешностей на систематические и случайные, а из положения о перерождении систематических погрешностей в случайные. Следовательно, при выборе метода суммирования погрешностей определяющим критерием должна являться степень корреляционной зависимости между соответствующими погрешностями.

Теория вероятностей, рассматривая погрешности как дисперсии случайных величин, для дисперсии суммы двух случайных величин даёт следующее выражение:

, (2.11)

где коэффициент r(τ) (2.10) определен при τ=0. Его значения изменяются от 0 (полная независимость появления погрешностей) до ±1 (погрешности жестко коррелированны).

При сильной взаимосвязи случайных погрешностей (r±1)

(2.12)

получаем правило алгебраического суммирования: суммарная погрешность равна алгебраической сумме отдельных погрешностей, а при r0

(2.13)

имеем правило геометрического суммирования: квадрат суммарной погрешности равен сумме квадратов погрешностей.