2. Порядок выполнения измерений

2.1. Определение расстояния между мнимыми источниками

2.1.1. Закрепив щель, бипризму и окулярный микрометр на заданных расстояниях L и d, регулировкой ширины щели и ее параллельности ребру бипризмы добиться четкой интерференционной картины.

2.1.2. Поместить линзу между бипризмой и окулярным микрометром. Перемещая линзу в направление бипризмы, добиться наличия увеличенного изображения мнимых источников света. Измерить с помощью окулярного микрометра расстояние l₁ по следующей методике:

2.1.2.1. С помощью ручки нониуса окулярного микрометра устанавливают перекрестие окуляра на «0» и совмещают «0» по шкале нониуса с риской нониуса (рис.5).

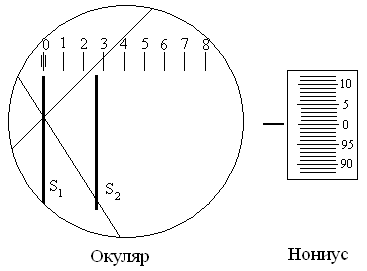
Рис. 5 Вид измерительных шкал окулярного микрометра

2.1.2.2. С помощью ручки перемещения салазок окулярного микрометра совмещают перекрестие микрометра с левым изображением мнимого источника света S₁.

2.1.2.3. С помощью ручки нониуса совмещают перекрестие с правым изображением мнимого источника света S₂ и записывают расстояние l₁ между S₁ и S₂:

l₁=N∙1+m∙0,01 (мм),

где N-число целых делений шкалы окуляра, m-число делений шкалы нониуса.

2.1.3. Перемещая линзу к окулярному микрометру, добиться наличия уменьшенного изображения мнимых источников света. Измерить расстояние l₂ аналогично п.п.2.1.2.1-2.1.2.3.

2.1.4. Измерения п.п. 2.1.2., 2.1.3 провести не менее 3 раз.

2.1.5. Измерения п.п. 2.1.1-2.1.5 провести для других расстояний d, заданных преподавателем.

2.1.6. Результаты измерений занести в самостоятельно разработанную таблицу.

2.2. Определение ширины интерференционной полосы

2.2.1. Отклонить линзу и измерить x по следующей методике:

2.2.1.1. Повторить п.2.1.1

2.2.1.2. С помощью ручки перемещения салазок окулярного микрометра совмещают перекрестие окулярного микрометра с серединой первого хорошо видимого левого интерференционного максимума (минимума).

2.2.1.3. С помощью ручки нониуса окулярного микрометра совмещают перекрестие с серединой 2, 3,…,11 максимума (минимума) интерференционной картины и записывают расстояние х_n между 1 и 2, 3,…,11 максимумом (минимумом) (целое число мм по шкале окулярного микрометра +десятые и сотые доли мм по шкале нониуса).

2.2.1.4. Определяют расстояние x, как , где n=1,2,…10 – количество максимумов (минимумов).

2.2.2. Измерения п.2.2.1 провести для других расстояний d, заданных преподавателем.

2.7. Результаты измерений занести в самостоятельно разработанную таблицу.

3. Обработка результатов измерений

3.1. Провести статистическую обработку результатов измерений l₁, l₂, Δx для каждого расстояния d.

3.2. Определить экспериментальное значение l по формуле (13) и сравнить его с результатом, полученным по формуле (10).

3.3. По формуле (9) определить значение λ_o для каждого расстояния d.

3.4. Расчитать доверительный интервал и относительную ошибку для λ_o (принять ∆l=0,01мм) для каждого расстояния d [5].

3.5. С помощью координатной оси сравнить полученные значения λ_o с табличными значениями длины волны для красного цвета.

Заключение

Сделать вывод о проделанной работе. Указать все полученные физические величины в виде: x_ист.=х±Δх, ε,  (ответ округлить по правилам).

Контрольные вопросы

1. Дать определения явления интерференции, когерентных волн, оптической длины пути, оптической разности хода.

2. Вывести условия максимумов и минимумов интерференции света.

3. Способы получения когерентных источников (метод Юнга, зеркала Френеля, бипризма Френеля).

4. Расчет интерференционной картины от двух источников.

5. Применение явления интерференции.

Изучение интерференционной схемы

получения колец Ньютона

Общие сведения

Интерференция – это явление, возникающее при сложении когерентных волн и состоящее в перераспределении интенсивности волн в пространстве, образовании минимумов в одних точках и максимумов в других. Наиболее простой способ получения интерференции лучей – это разделить один луч на два, а затем сложить их в точке наблюдения.

Основные проявления: интерференция в тонких плёнках (равного наклона) и интерференция в клине (равной толщины). В обоих случаях интерференция происходит при сложении отражённого и преломленного лучей вблизи границы раздела двух оптически разнородных сред.

Схема прохождения лучей при интерференции в клине показана на рис. 1. Падающий на клин луч 1 разделяется на два когерентных луча, один (луч 2) образуется при преломлении падающего луча, другой (луч 3) при отражении. Эти лучи, пройдя по различной траектории, пересекаются в точке D, где и происходит интерференция.

Рис. 1. Схема получения интерференции в клине

В случае малых величин угла падения  и угла клина  интерференция происходит вблизи поверхности клина. Оптическая разность хода  лучей 2 и 3 определяется как =(AB+BC)n_k+(CD –AD)n_c-/2, где n_k – показатель преломления материала клина; n_c – показатель преломления среды над клином. Член /2 возникает за счёт «потери полволны» (запаздывания фазы) в случае, если луч отражается при переходе из среды с меньшим показателем преломления (менее оптически плотной) в среду с большим показателем преломления (более оптически плотную). При малых  и  ADCD и ABBCd. Тогда

=2dn_k – , (1)

где d – толщина клина в точке B.

В этом случае выражения для интерференционных максимумов и минимумов имеют следующий вид:

(2)

где k=0,1,2,… – порядок интерференционного максимума и минимума.

Из формулы (2) видно, что интерференционные максимумы и минимумы соответствуют определённым толщинам клина, образуя интерференционные полосы, что и определило название интерференции – равной толщины. Для плоского клина полосы будут располагаться параллельно ребру, образованному соединением плоскостей.

Частным случаем интерференции на клине является интерференция в сферической линзе, помещённой на плоское стекло. В этом случае интерференционные полосы образуют замкнутые окружности, называемые кольцами Ньютона. Схема интерференции на сферической линзе показана на рис. 2.

Рис. 2. Схема хода лучей при интерференции на сферическом клине,

образованном линзой и пластиной

Луч 1 падает перпендикулярно плоской поверхности линзы. Интерференция наблюдается при сложении лучей 2 и 3, образованных при разделении луча 1 в точке А. Луч 2 образуется при отражении от поверхности линзы в точке А, луч 3 – при преломлении в той же точке. Как и в плоском клине, в случае интерференции на линзе, при малом угле падения  (это выполняется в случае большого радиуса линзы), интерференция будет наблюдаться вблизи сферической поверхности линзы. В данном случае образуется воздушный клин и луч 3 распространяется в воздушной среде, следовательно, показатель преломления клина n_k =1. Для малого угла  АВВСd, ADCD и формула (1) преобразуется:

= 2d+ .

Тогда для толщины слоёв линзы d, соответствующих максимумам и минимумам интерференции, выполняется соотношение:

; (3)

(очевидно, что максимум 0 – го порядка отсутствует).

Условие (3) определяет условия образования светлых (максимум) и тёмных (минимум) колец на поверхности линзы.

Рис.3. Схема для вывода радиуса кольца, соответствующего минимуму k-го порядка

Используя рис. 3, можно увидеть, что радиус тёмного кольца, соответствующего минимуму k – го порядка, находится по формуле:

, (4)

где R – радиус линзы.

Формула (4) выведена в предположении отсутствия зазора между линзой и пластиной, чего достичь на практике достаточно сложно из-за попадания на пластину мелких пылинок и возникновения царапин. Можно исключить вклад зазора в расчётную формулу, если использовать значение двух различных радиусов тёмных колец r_k и r_i. В этом случае расчётная формула для длины волны падающего света  примет следующий вид:

, (5)

где k и i – порядки интерференционных колец.

Формула (5) справедлива как для интерференционных минимумов, так и для интерференционных максимумов.