Определение главного фокусного расстояния линз Общие сведения

Линзы представляют собой прозрачные тела, ограниченные двумя поверхностями (сферой или плоскостью), преломляющими световые лучи, способные формировать оптические изображения предметов. Линза называется тонкой, если ее толщина (расстояние между ограничивающими поверхностями) значительно меньше радиусов поверхностей, ограничивающих линзу. Прямая, проходящая через центры кривизны поверхностей линзы, называется главной оптической осью О₁О₂ (рис.1). Точка, лежащая на пересечении линзы с главной оптической осью и обладающая свойством, что лучи проходящие через нее не преломляются, называется оптическим центром линзы О (рис.1). Фокус F- это точка, в которой после преломления собираются все лучи (или продолжение лучей), падающие на линзу параллельно главной оптической оси (рис.1). Расстояние от оптического центра до фокуса, называется фокусным расстоянием.

а)

б)

Рис. 1. Ход лучей, идущих параллельно главной оптической оси:

а) собирающая линза; б) рассеивающая линза

Построение изображения предмета в линзах осуществляется по следующей схеме (рис.2):

1. луч, проходящий через оптический центр линзы, не изменяет своего направления (луч 1);

2. луч, идущий параллельно главной оптической оси; после преломления в линзе (или его продолжение) проходит через второй фокус линзы (луч 2);

3. луч (или его продолжение), проходящий через фокус линзы; после преломления в ней выходит из линзы параллельно ее главной оптической оси (луч 3).

а)

б)

Рис.2. Построение изображений в линзах:

а) собирающая линза; б) рассеивающая линза

Плоскость, перпендикулярная главной оптической оси и проходящая через главный фокус, называется фокальной плоскостью. Параллельный пучок лучей, идущий под углом ≠0^о к главной оптической оси, после прохождения через линзу собирается в одной из точек фокальной плоскости – т.F′ (рис.3), называемой побочным фокусом. Чтобы определить положение этой точки, нужно провести луч, идущий через центр линзы и параллельный данному пучку, до пересечения его с фокальной плоскостью – луч OF′ (рис.3). Через точку пересечения F′ пройдут и остальные лучи.

а)

б)

Рис.3. Ход лучей, идущих под углом ≠0^о к главной оптической оси:

а) собирающая линза; б) рассеивающая линза

Для тонкой линзы справедлива следующая формула:

(1)

где f – фокусное расстояние линзы (f>0, если линза собирающая, f<0, если линза рассеивающая);

a– расстояние от предмета до линзы;

b – расстояние от линзы до изображения предмета (b>0, если изображение действительное, b<0, если изображение мнимое);

n₂₁ – относительный показатель преломления;

R_1, R₂- радиусы кривизны поверхностей линзы (R>0, если поверхность выпуклая, R<0, если поверхность вогнутая).

Величина называется оптической силой линзы. Единицей измерения оптической силы является диоптрия: .

Следующая важная характеристика линзы – диаметр линзы или апертура. Если линза ограничена диафрагмой, то под апертурой следует понимать диаметр диафрагмы d. Отношение апертуры к ее главному фокусному расстоянию 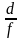называется относительным отверстием линзы. Отношение квадрата апертуры к квадрату фокусного расстояния называется светосилой линзы.

Фокусное расстояние собирающей линзы может быть определено разными способами.

Способ 1. Определение фокусного расстояния по расстоянию от предмета до линзы и от линзы до изображения предмета.

Из соотношения (1) получим:

.

(2)

Способ 2. Определение фокусного расстояния по величине предмета и его изображения и по расстоянию от линзы до изображения предмета.

Коэффициент увеличения линзы

,

(3)

где h – величина предмета;

H – величина изображения предмета.

Выразив расстояние от предмета до линзы из соотношения (3) и подставив его в формулу (1), получим фокусное расстояние линзы:

.

(4)

Способ 3. Определение фокусного расстояния по расстоянию от предмета до его изображения и по величине перемещения линзы.

Если расстояние А от предмета до изображения более 4f, то всегда найдутся два положения линзы, при которых на экране получается отчетливое изображение предмета: в одном случае уменьшенное, в другом увеличенное (рис.4). Нетрудно доказать, что оба положения линзы будут симметричны относительно середины расстояния между предметом и изображением.

Рис.4. Построение увеличенного и уменьшенного изображения предмета, не изменяя расстояния А

Рассмотрим одно из положений линзы, для которого расстояние от предмета до линзы – , а расстояние от линзы до изображения – . Подставив значения а и b в формулу (2), получим следующее фокусное расстояние линзы: . (5) Оптическая сила системы N линз, при условии, что расстояние между линзами много меньше

фокусного расстояния этой системы линз, равна:

.

(6)

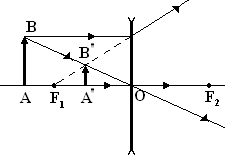
Рассеивающая линза всегда дает мнимое изображение предмета, поэтому вычислить фокусное расстояние описанными способами невозможно. Для его определения используем вспомогательную собирающую линзу, для которой D₁> (D₁ – оптическая сила собирающей линзы, 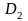– оптическая сила рассеивающей линзы). При этом условии . Тогда, определив оптическую силу собирающей линзы и оптическую силу системы линз, можно вычислить оптическую силу рассеивающей линзы:

.

(7)

Лабораторная работа № 3.1

ОПРЕДЕЛЕНИЕ ГЛАВНОГО ФОКУСНОГО

РАССТОЯНИЯ ЛИНЗ

Цель работы: различными методами определить фокусное расстояние собирающей и рассеивающей линз, составить технические характеристики линз.

1. Описание установки

Установка состоит из оптической скамьи 1, осветителя с нанесенной на нем шкалой 2, собирающей и рассеивающей линзы 3, экрана 4 (рис.5).

Рис. 5. Схема установки

Шкала, нанесенная на осветитель, выполняет роль предмета, изображение которого получается с помощью изучаемых линз. Все приборы устанавливаются так, чтобы их центры лежали на одной горизонтальной оси. Расстояние между приборами отсчитывается по шкале, нанесенной на оптической скамье.