10. Предельный переход для формулы Бернулли
-локальная теорема Лапласа: Pn(m)=1/√npq * Ф(x). X=(m-np)/ √npq, Ф(x) – четная, Ф(-x)= Ф(x). Ф(x>4)=0, n,m – большие числа. Ф(x)= 1/√2П * e-x2/2, lim √npq* Pn(m) / Ф(x) = 1
Pn(m) = n!/m!(n-m)! * pmqn-m- cмысл теоремы.
Если
вер-сть р наступления соб. А в каждом
испытании постоянна и отлична от 0 и 1,
то вер-сть Pm,n
того, что соб. А произойдет m
раз в n
независ. испытаниях при n→∞
≈:
,
где
-
ф-я Гаусса, и
.
Если np>0,
npq<20,
то эта ф-ла считается приближенно.
Свойства
ф-и f(x):
1.f(x)
четная, т.е. f(-x)=
f(x);
2. f(x)
- монотонно убывающая при х>0, причем
при х →∞, f(x)→0.
-интегральная теорема Лапласа: Pn(m1≤m≤m2)= Ф(x2) - Ф(x1)/ Ф(x)- функция Лапласа. X1=(m1 – np) / √npq, x2= (m2 – np)/ √npq
Ф(-x)= -Ф(x), Ф(x>4)=0,5.
Pn(m1≤m≤m2)=∑n!/m!(n-m)! * pmqn-m
P(a≤(m-np)/ √npq≤b)= 1/√2П * ∫e-x2/2dx
Если
вер-сть р наступл-я соб. А в каждом
испытании постоянна и отлична от 0 и 1,
то вер-сть того, что число m
наступл-я соб. А в n
независ. испытаниях заключено в пределах
от а до b
(включительно), при n→∞
≈:
Pn(a≤m≤b)≈0,5[Ф(x2)-Ф(x1)],
где
-
ф-я Лапласа,
,
,
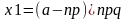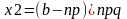испол-ся при тех же условиях, что и
локальная. Свойства
ф-и Ф(х):
1. Ф(х) нечетная, т.е. Ф(-х) = -Ф(х); 2. Ф(х)
монотонно возрастающая, причем при х→∞
Ф(х)→1.
11. Теорема Пуассона. Простейший поток событий, его свойства
n→∞, np=a, следовательно, lim pn(k)=ak/k! * e-a.
Теорема.
Если вер-сть р наступления соб. А в
каждом испытании →к 0 при n→∞,
причем произведение np
→к постоянному числу λ, то вероятность
Pm,n
того, что соб. А появится m
раз в n
независимых испытаниях, удовлетворяет
предельному равенству
.
По ф-ле Бернулли Pm,n=
pmqn-m;
=n!\(n-m)!m!=n(n-1)...(n-m+1)\m!
– подставляем в ф-лу Бернулли и учитывая,
что lim
np=
λ (при n→∞),
т.е. при достаточно больших n,
p≈
λ\n.
Подставляем рm=
(λ\n)m.
Pm,n=(λm\m!)*[1*(1-1\n)(1-2\n)…(1-(m-1)\n)]*(1-
λ\n)n(1-
λ\n)-m.
Т.к. lim(1-1\n)=lim(1-2\n)=…=lim(1-(m-1)\n)=1
(при
n→∞), а
lim(1- λ\n)n=e-λ
и
lim(1- λ\n)-m=1,
то
limPm,n= λme-λ\m!
Но
согласно условия теор. Пуассона: р→0,
n→∞,
np→λ,
λ≤10, то Pm,n≈
λme-λ
\
m!.
Простейший поток событий: поток событий – последовательность событий, происходящих в случайные моменты времени. Простейший поток – поток, для которого характерны признаки: 1.он стационарен; 2.он должен характеризоваться ординарностью. Если dt→0 , то произойдет 1 событие; 3. Отсутствие после действия.
Если 3 признака выполняются, то характеристика потока: интенсивность – среднее число события в потоке в единицу времени (λ). Pt(k)= (λ t)k/k! * e-λt
12. Св. Закон распределения св
СВ – действительная функция Х(w), отображающая Ω в Ωх R так, что прообразы событий из Fx лежат в F, т.е. являются событиями из F. Это величина, которая в результате единичного испытания принимает единственно возможное значение, не известное заранее. Случайная величина - переменная, котор. в результате испытания в зависимости от случая принимает одно из возможного множества своих значений (какое именно заранее не известно). Случайная величина наз-ся дискретной (прерывной), если множ-во ее значений конечное, или бесконечное, но счетное. Множество называется счетным, если его эл-ты можно перенумеровать натуральными числами. Непрерывная случ. величина - величина, бесконечное несчетное множество значений котор. есть некоторый интервал (конечный или бесконечный) числовой оси. Закон распределения СВ – любое правило, позволяющее нам перечислять все возможные значения СВ и указать вероятности их появления. Это всякое соотношение, устанавливающее связи между возможными значениями СВ и их вероятностями