Выполнение:

Во многих случаях представляет интерес не получение точеной оценки неизвестного параметра распределения, а указание области (например, интервала на числовой прямой), в которой этот параметр находится с вероятностью, не меньшей заданной. Statgraphics позволяет строить такие области.

ЗАДАНИЕ:

Требуется:

1) получить 10 случайный выборок объема n=100 из нормальной генеральной совокупности N(0,1);

2) построить по каждой из полученных выборок три доверительных интервала для математического ожидания M:

a) с доверительной вероятностью P=95%

b) с доверительной вероятностью P=90%

c) с доверительной вероятностью P=70%

3) выяснить, как часто доверительный интервал не накрывает истинное значение математического ожидания M=0 в случае a), в случае b), в случае c).

4) проанализировать, как зависит длина доверительного интервала от величины P;

5) сгенерировать 5 случайных выборок из N(0,1) с объемами n=10,30,50,100,1000;

6) построить для каждой из пяти выборок доверительные интервалы с одной и той же доверительной вероятностью P=95%

a) для математического ожидания M;

b) дисперсии σ²

7) проанализировать, как зависит длина доверительного интервала от объёма выборки в обоих случаях.

Для получений десяти нужных выборок используйте генератор случайных чисел. Заготовьте в тетради таблицу:

Название выборки	Доверительный Интервал для P=0,95	Его длина	Доверительный Интервал для P=0,90	Его длинна	Доверительный Интервал для P=0,7	Его длина

Построение доверительных интервалов

В строке меню выберите Analyze(Анализ), в раскрывшемся меню выберите Variable Data(Числовые данные), затем One-Variable Analysis (Анализ одной переменной).

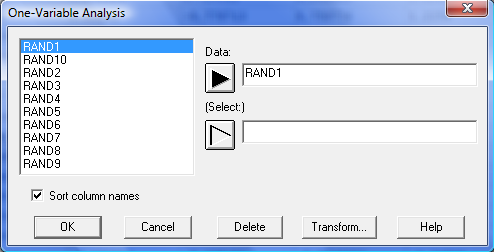
Рис. 3.1

В раскрывшемся окне (Рис.3.1) выберите название выборки, затем нажмите на кнопку , нажмите ОК.

Нажмите кнопку Tables (таблицы), раскроется диалоговое окно (рис. 3.2)

Рис. 3.2

выберите в нем Confidence Intervals(Доверительный интервалы), нажмите ОК. Перед вами появится новое окно, щёлкните по нему дважды, чтобы раскрыть. В этом окне вы можете увидеть данные: доверительный интервал для 95% вероятности для мат. ожидания и дисперсии. Вам нужен доверительный интервал для P=90%. Щелкните правой кнопкой в этом окне, выберите Pane Options(Настройка границ), в раскрывшемся окне наберите нужные цифры, нажмите ОК.

Выполните операцию и занесите в таблицу данные доверительного интервала с точностью до двух знаков после десятичной запятой, вычислите его длину. Повторите тоже самое для P=70%.

Аналогично заполните таблицу для остальных девяти выборок.

Посчитайте, во скольких случаях из десяти истинное значение мат. ожидания M=0 оказалось вне доверительного интервала для P=95%, P=90%, а затем для P=70%. В каком случае это происходит чаще?

Покажите результаты преподавателю.

Сгенерируйте сейчас опять пять выборок из нормальной совокупности N(0,1) для n=10,30,50,100,1000. постройте для каждой из этих выборок доверительные интервалы для мат.ожидания и дисперсии с доверительной вероятностью 95%. Заполните следующую таблицу:

Объем выборки	Доверительный интервал для M	Его длина	Доверительный интервал для σ2	Его длина

Как изменяются длины доверительных интервалов при зафиксированной доверительной вероятности с увеличением объема выборки?

Покажите результаты преподавателю.