Задание

1. Сгенерируйте 5 выборок из нормально распределенной генеральной совокупности размером 10, 50, 100, 500, 1000 каждая. Для каждой вы­борки постройте гистограмму. Покажите преподавателю.

Вопросы к лабараторной работе

1. Каков содержательный смысл распределения Бернулли?

2. Каков содержательный смысл равномерного распределения?

3. Почему в приложениях чаще других встречается нормальное рас­пределение?

4. Статистическим аналогом какой вероятностной кривой является гистограмма частостей? Полигон частостей? Кумулянта?

5. Что такое распределение Стьюдента? χ ²? Фишера?

6. Какой смысл имеют параметры a, b в распределении N(a,b)?

7. Что происходит с графиком плотности нормального распределения, если увеличивать мат.ожидание? Дисперсию?

8. Что происходит с графиком плотности распределения Стьюдента при увеличении числа степеней свободы?

9. Что происходит с графиком плотности распределения χ ² при увели­чении числа степеней свободы?

Лабораторная работа №3. Построение доверительных интервалов. Теоретический минимум.

1) Доверительный интервал- это интервал, построенный с помощью случайной выборки из распределения с неизвестным параметром, такой, что он содержит данный параметр с заданной вероятностью.

Пусть есть выборка из распределения , где - неизвестный параметр. Пусть также задана достоверность (желаемая вероятность попадания) . Тогда случайный интервал [L,U], где

есть некоторые статистики имеющейся выборки, такой, что

,

называется α - доверительным интервалом для параметра θ.

В приложениях вместо α часто используется . Например, термины 0.95-доверительный интервал и - доверительный интервал равнозначны.

Параметр α (или ) называется степенью доверия интервала [L,U].

2) Доверительный интервал для математического ожидания нормальной выборки.

Случай известной дисперсии.

Пусть - независимая выборка из нормального распределения, где σ2 - известная дисперсия. Определим произвольное и построим доверительный интервал для неизвестного среднего μ.

Утверждение. Случайная величина

имеет стандартное нормальное распределение N(0,1). Пусть z_α - α-процентиль стандартного нормального распределения. Тогда в силу симметрии последнего имеем:

.

После подстановки выражения для Z и несложных алгебраических преобразований получаем:

.

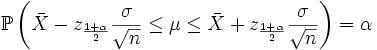Случай неизвестной дисперсии.

Пусть - независимая выборка из нормального распределения, где μ,σ2 - неизвестные константы. Построим доверительный интервал для неизвестного среднего μ.

Утверждение. Случайная величина

,

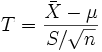где S - несмещённая выборочная дисперсия, имеет распределение Стьюдента с n − 1 степенями свободы t(n − 1). Пусть t_α,n − 1 - α-процентиль этого распределения. Тогда в силу симметрии последнего имеем:

.

После подстановки выражения для T и несложных алгебраических преобразований получаем:

.