Задание

1. Число пассажиров компании «Уральские авиалинии» одного из рей­сом между Екатеринбургом и Москвой за 30 дней между апрелем и ма­ем текущего года составило:

121 134 118 123 109 120 116 125 128 121 129 130 131 127 119 114 124 11О 126 134 125 128 123 133 132 136 134 129

От Вас требуется:

а) Просмотреть выборку на экране

б) Произвести интервальную группировку данных (построить интер­вальные вариационные ряды частот, частостей, накопленных частот и накопленных частостей);

в) Построить гистограмму, полигон и кумуляту частостей;

г) Вычислить выборочные числовые характеристики: среднее, моду, медиану, размах, дисперсию, стандартное отклонение, асимметрию, эксцесс.

Результат покажите преподавателю.

2. Рассмотрим данные, набранные в файле Cardata.sf.

От Вас требуется:

а) Просмотреть выборку на экране

б) Произвести интервальную группировку данных (построить интер­вальные вариационные ряды частот, частостей, накопленных частот и накопленных частостей);

в) Построить гистограмму, полигон и кумуляту частостей;

г) Вычислить выборочные числовые характеристики: среднее, моду, медиану, размах, дисперсию, стандартное отклонение, асимметрию, эксцесс.

Результат покажите преподавателю.

Вопросы к лабараторной работе

1. Как записывается выборочное среднее для не сгруппированных

данных?

2. Как записывается несмещенная выборочная дисперсия для не сгруппированных данных

3. Что такое мода (можно на примере)

4. Что такое медиана (можно на примере)

5. Что характеризуют асимметрия и эксцесс?

6. Для чего используется коэффициент вариации?

7. Что Вы понимаете под репрезентативностью выборки?

Лабораторная работа №2 Связь статистики с теорией вероятности.

Генератор случайных чисел.

Теоретический минимум

1) Генеральная совокупность (в англ. — population) — совокупность всех объектов (единиц), относительно которых учёный намерен делать выводы при изучении конкретной проблемы. Генеральная совокупность состоит из всех объектов, которые подлежат изучению. Состав генеральной совокупности зависит от целей исследования. Иногда генеральная совокупность - это все население определённого региона (например, когда изучается отношение потенциальных избирателей к кандидату), чаще всего задаётся несколько критериев, определяющих объект исследования. Например, женщины 10-89 лет, использующие крем для рук определённых марок не реже раза в неделю, и имеющие доход не ниже $150 на одного члена семьи.

2) Средним отклонение θ называют среднее арифметическое отклонений:

θ=(∑n_i |x_i- _в|)/∑n_i

Например, для ряда

x_i 1 3 6 16

n_i 4 10 5 1

имеем:

_в=(4∙1+10∙3+5∙6+1∙16)/(4+10+5+1)=80/20=4

θ=(4∙|1-4|+10∙|3-4|+5∙|6-4|+1∙|16-4|)/20=2,2

Среднее отклонение служит для характеристики рассеяния вариационного ряда.

3) Нормальным называется распределение, которое описывается функцией плотности вида

Р(х)=

Множитель удовлетворяет условию нормировки

Обычно выделяют стандартное нормальное распределение, имеющее

m_n=0, : p_H(x)= .

Кривая стандартного нормального распределения симметрична относительно оси ординат и имеет вид, представленный на рисунке 2.1

Рис. 2.1 Стандартное нормальное распределение

Интеграл от плотности вероятностей не выражается через элементарные функции. Для расчета вероятностей случайных величин с нормальным распределением составлены таблицы специальной функции, известной как Лапласа:

Ф(х)= dx.

Поскольку вычислить некоторую вероятность Р( )= для нормального распределения невозможно, используются некоторые специальные преобразования, которые позволяют найти искомую вероятность

Р( )=Ф( .

4) Отклонением называют разность между случайной величиной и ее математическим ожиданиям.

К наиболее известным законам распределения дискретной случайной величины относятся ряд законов, описываемых определенными аналитическими зависимостями.

5) Биноминальный закон описывается при помощи так называемой формулы Бернулли Р_n(k)=C_n^k р^k q^n-k.

Закон назван биноминальным, так как в правой части записан общий член разложения Ньютона

(р+q)ⁿ=Cⁿ_nрⁿ+C^n-1_np^n-1q+…+C⁰_nqⁿ.

Первый член разложения рⁿ определяет вероятность наступления рассматриваемого события n в n-независимых испытаний и т.д.

Закон Пуассона Р_n(к)= используется в схеме Бернулли при n .

равномерное распределение. Данное распределение непрерывной случайной величины на некотором интервале ( задается формулой

р(х)=

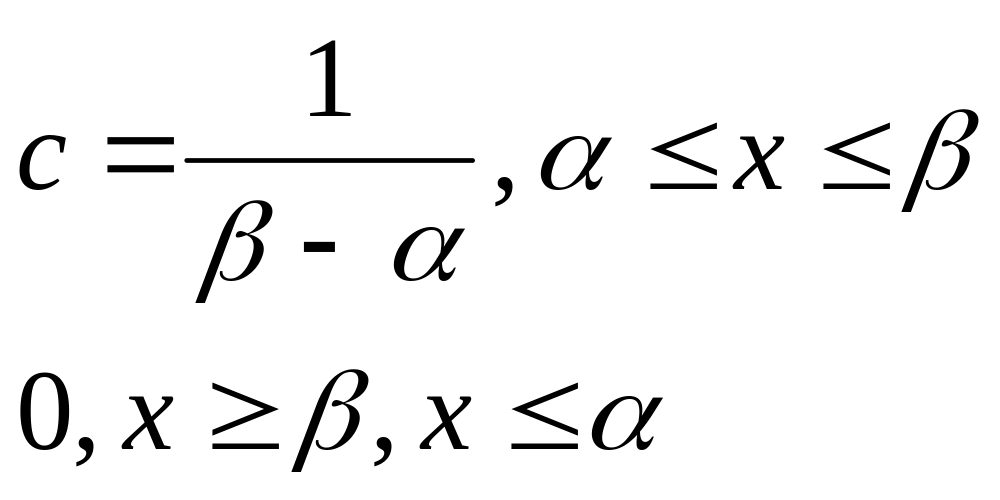
Для случайной величины , равномерно распределенной в интервале ( , вероятность попадания в любой интервал (х₁,х₂),лежащий внутри ( , пропорциональна длине этого интервала р(х₁< <x₂)=с(х₂-х₁);

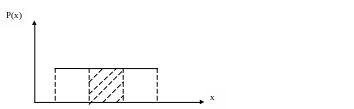
х₁ х₂

Рис. 2.2 Функция плотности равномерной случайной величины

6) Распределение Стьюдента.

t= ,

t- есть распределение Стьюдента с =n-1 степенями свободы.