Методические указания по выполнению самостоятельных работ по твмс на ппп статграф с

Темы самостоятельных работ:

№1 Ввод, первичная обработка и графическое представление статистических данных.

№ 2.

Теоретический минимум.

1) Пусть из генеральной совокупности извлечена выборка, причем x₁ наблюдалось n₁ раз, x₂-n₂ раз, x_k-n_k раз ∑n_i=n- объем выборки. Наблюдаемые значения x_i называют вариантами, а последовательность вариант, записанных в возрастающем порядке,- вариационным рядом. Числа наблюдений называют частотами.

Выборка — множество случаев (испытуемых, объектов, событий, образцов), с помощью определённой процедуры выбранных из генеральной совокупности для участия в исследовании.

Объём выборки — число случаев, включённых в выборочную совокупность. Из статистических соображений рекомендуется, чтобы число случаев составляло не менее 30—35.

2) Модой M₀ называют варианту, которая имеет наибольшую частоту. Например, для ряда

варианта…….1 4 7 9

частота …….5 1 20 6

мода равна 7.

3) Медианой m_e называют варианту, которая делит вариационный ряд на две части, равные по числу вариант. Если число вариант нечетно, т.е. n=2k+1, то m_e=X_k+1; при четном n=2k медиана

M= (X_k+X_k+1)/2.

Например, для ряда 2 3 5 6 7 медиана равна 5; для ряда 2 3 5 6 7 9 медиана равна (5+6)/2=5,5.

4) Дисперсией дискретной случайной величины называют математическое ожидание квадрата отклонения случайной величины от ее математического ожидания. Отклонением будем называть случайную величину, равную -M{ }:

D { } =M { -M { }}².

Дисперсию можно интерпретировать, как меру разброса значений случайной величины относительно ее математического ожидания.

Для вычисления дисперсии значительно более удобна другая формула:

D{ }=M{ ²}-M²{ }. Справедливость формулы (1.14) нетрудно доказать. Действительно,

D { } =M{ ²-2M{ } +M²{ }}.

Используя свойство аддитивности математического ожидания, запишем

D { } =M { ²}-2M { }M{ } +M²{ }.

И окончательно D{ }=M{ ²}-M²{ }, что и требовалось доказать.

D{ } обладает следующими свойствами:

1. D{c}=0

2. D{c }=c²D{ }

3. D{ +Y}=D{ }+D{Y}

для независимых случайных величин.

5) Среднее (математическое ожидание).

,где

М(Х)-математическое ожидание;Р_i-вероятность i-того события; х_i-i-тое испытание.

В статистике применяется выборочное среднее:

Преимущества: если эксперимент повторяется многократно, а результаты суммируются (например, в страховании, азартных играх), математическое ожидание — естественный выбор.

Недостатки: не соответствует интуитивному пониманию «среднего»; меньшинство с аномальными значениями (долгожители, миллиардеры, бракованные изделия и т. д.) серьёзно смещают мат.ожидание. В статистических расчётах рекомендуется отбрасывать такой «хвост»

6) Размахом варьирования R называют разность между наибольшей и наименьшей вариантами:

R=X_max-X_min .

Например, для ряда 1 3 4 5 6 10 размах равен 10-1=9.

Размах является простейшей характеристической рассеяния вариационного ряда.

7) Асимметрией теоретического распределения называют величину А_s=

где - называется центральным моментом третьего порядка, а σ³ :

,где

p(x)- плотность распределения вероятностей;

Практически определяют знак асимметрии по расположению кривой распределения относительно моды (для нормального распределения мода-значение аргумента х, при котором совпадает с математическим ожиданием). Если длинная часть кривой распределения расположена правее моды, то асимметрия положительна, в противном случае - отрицательна (рис.1.1).

Р(х)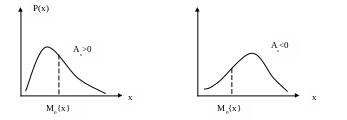

Рис.1.1 Распределение с положительной и отрицательной асимметрией

8) Эксцессом теоретического распределения называют характеристику, которая определяется равенством

Е_к= , где

.

Для нормального распределения =3,где

p(x)- плотность распределения вероятностей.

Если эксцесс Е_к>0, то распределение имеет более «высокую» и «острую» вершину, чем нормальное распределение и наоборот, если Е_к<0 (рис. 1.2).

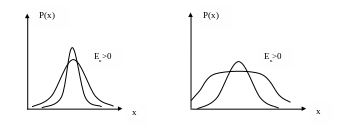
Рис.1.2 Эксцесс теоретического распределения

9) Нормальным называется распределение, которое описывается функцией плотности вида

Р(х)=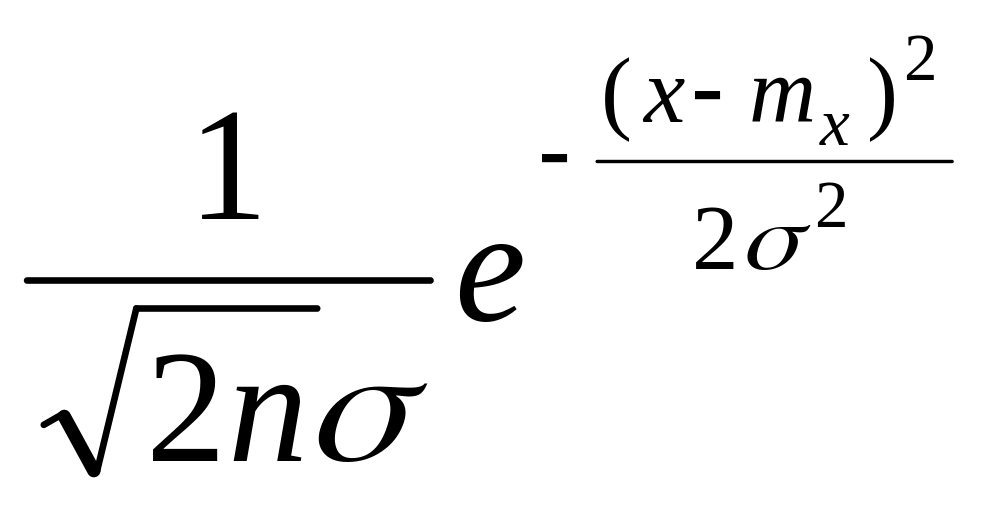

Множитель удовлетворяет условию нормировки

Обычно выделяют стандартное нормальное распределение, имеющее

m_n=0, : p_H(x)= .

Кривая стандартного нормального распределения симметрична относительно оси ординат и имеет вид, представленный на рисунке 2.1

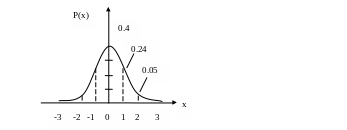
Рис. 2.1 Стандартное нормальное распределение

Интеграл от плотности вероятностей не выражается через элементарные функции. Для расчета вероятностей случайных величин с нормальным распределением составлены таблицы специальной функции, известной как Лапласа:

Ф(х)=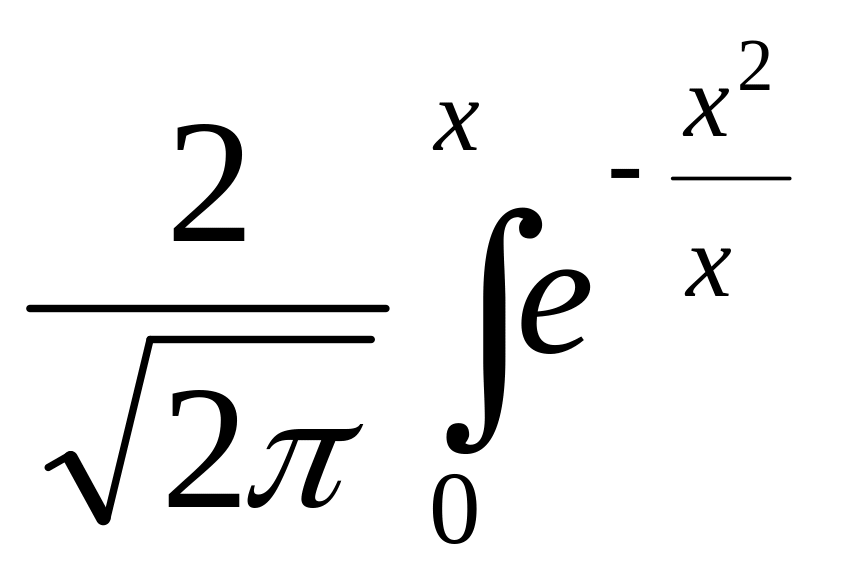 dx.

Поскольку вычислить некоторую вероятность Р( )= для нормального распределения невозможно, используются некоторые специальные преобразования, которые позволяют найти искомую вероятность

Р( )=Ф( .

10) Стандартное отклонение (иногда среднеквадратичное отклонение) — в теории вероятности и статистике наиболее распространенный показатель рассеивания значений случайной величины относительно её математического ожидания. Измеряется в единицах измерения самой случайной величины. Равен корню квадратному из дисперсии случайной величины. Стандартное отклонение используют при расчёте стандартной ошибки среднего арифметического, при построении доверительных интервалов, при статистической проверке гипотез, при измерении линейной взаимосвязи между случайными величинами.

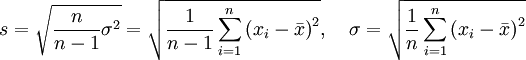
где — стандарт, стандартное отклонение, несмещенная оценка среднеквадратического отклонения случайной величины X относительно её математического ожидания; — дисперсия; — i-й элемент выборки; — среднее арифметическое выборки; — объём выборки.

Следует отметить отличие стандарта (в знаменателе n − 1) от корня из дисперсии (среднеквадратического отклонения) (в знаменателе n), при малом объёме выборки оценка дисперсии через последнюю величину является несколько смещенной, при бесконечно большом объёме выборки разница между указанными величинами исчезает. Выборка — лишь часть генеральной совокупности. Генеральная совокупность — абсолютно все возможные результаты. Получить результат, не входящий в генеральную совокупность абсолютно невозможно в принципе. Для случая с бросанием монетки генеральной совокупностью является: решка, ребро, орел. А вот пара орел-решка уже лишь выборка. Для генеральной совокупности математическое ожидание совпадает с истинным значением оцениваемого параметра. А вот для выборки не факт. Математическое ожидание выборки имеет смещение относительно истинного значения параметра. В силу этого, среднеквадратичная ошибка больше чем дисперсия, так как дисперсия — математическое ожидание квадрата отклонения от среднего значения, а среднеквадратичное отклонение — математическое ожидание отклонения от истинного значения. Разница в том, от чего ищем отклонение, когда дисперсия, то от среднего и не важно истинное это среднее или ошибочно, а когда среднеквадратичное отклонение, то ищем отклонение от истинного значения.

Правило 3-х сигм ( ) — практически все значения нормально распределённой случайной величины лежат в интервале . Более строго — не менее чем с 99,7 % достоверностью, значение нормально распределенной случайной величины лежит в указанном интервале. При условии, что величина истинная, а не полученная в результате обработки выборки. Если же истинная величина неизвестна, то следует пользоваться не σ, а s. Таким образом, правило 3-х сигм преобразуется в правило трех s.

11) Коэффициент вариации случайной величины — мера относительного разброса случайной величины; показывает, какую долю среднего значения этой величины составляет ее средний разброс.

Равен отношению стандартного отклонения к математическому ожиданию.

Так же используется такие обозначение:

В отличие от среднего квадратического или стандартного отклонения измеряет не абсолютную, а относительную меру разброса значений признака в статистической совокупности. Исчисляется в процентах. Вычисляется только для количественных данных.