
- •6. Обчислити інтеграл :
- •8. Обчислити границю ;
- •9. Розв'язати диференціальне рівняння .
- •6. Обчислити границю :
- •7. Обчислити інтеграл :
- •9. Розв'язати диференціальне рівняння .
- •7. Обчислити інтеграл :
- •8. Обчислити границю ;
- •9. Розв'язати диференціальне рівняння .
- •6. Обчислити границю :
- •9. Розв'язати диференціальне рівняння .
- •8. Обчислити границю ;
- •9. Розв'язати диференціальне рівняння .
- •5. Знайти , якщо , .
- •8. Знайти диференціал функції .
- •9. Розв'язати диференціальне рівняння .
- •8. Обчислити границю ;
- •9. Розв'язати диференціальне рівняння .
- •5. Знайти , якщо .
ВАРІАНТ 1.
1. Визначник другого порядку обчислюється за формулою:
а)
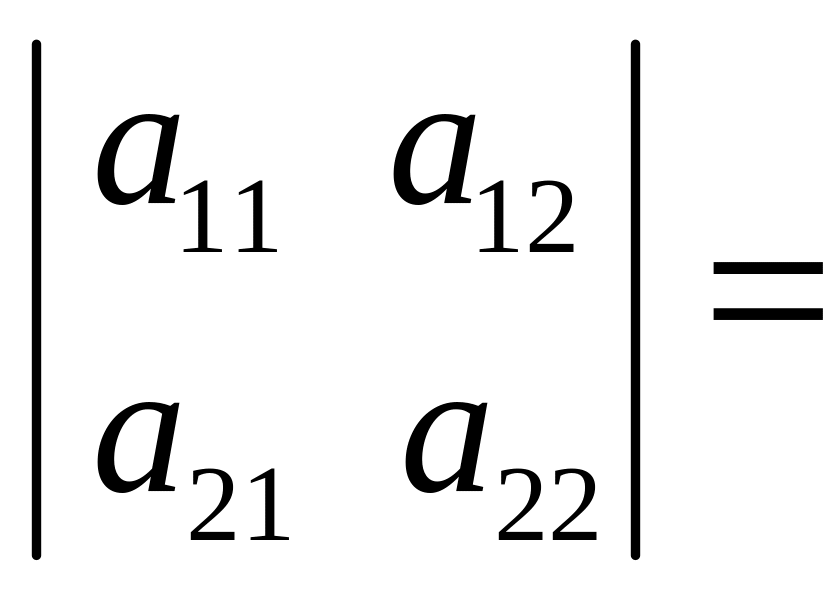
![]() ,
б)
,
б)
![]() ,
,
в)
![]() ,
г)
,
г)
![]() .
.
2. Якщо
в точці
![]() функція
функція
![]() не має, принаймні, однієї з однобічних
границь, або хоча б одна з однобічних
границь є нескінченною, то точка
називається
не має, принаймні, однієї з однобічних
границь, або хоча б одна з однобічних
границь є нескінченною, то точка
називається
а) усувною точкою розриву, б) точкою розриву першого роду,
в) точкою розриву другого роду, г) точкою неперервності функції.
3. У
формулі інтегрування за частинами
невизначений інтеграл
![]() дорівнює
дорівнює
а)
![]() ,
б)
,
б)
![]() ,
в)
,
в)
![]() ,
г)
,
г)
![]() .
.
4. Якщо
характеристичне рівняння має два
однакові корені
![]() ,
то загальний розв'язок диференціального
рівняння
,
то загальний розв'язок диференціального
рівняння
![]() має вигляд:
має вигляд:
а)
![]() ,
б)
,
б)
![]() ,
,
в)
![]() ,
г)
,
г)
![]() .
.
5. Обчислити
границю
![]() :
:
а) ![]() ,
б)
,
б) ![]() ,
в)
,
в) ![]() ,
г)
інша відповідь.
,
г)
інша відповідь.
6. Знайти
диференціал функції
![]() :
:
а) ![]() ,
б)
,
б) ![]() ,
,
в) ![]() ,
г)
інша відповідь.
,
г)
інша відповідь.
7. Обчислити
інтеграл
![]() :
:
а) ![]() ,
б) 3,
в) 4, г)
інша відповідь.
,
б) 3,
в) 4, г)
інша відповідь.
8. Знайти
добуток
![]() ,
якщо
,
якщо
![]() ,
,
![]() ;
;
Відповідь:
![]() .
.
9. Розв'язати
диференціальне рівняння
![]() .
.
Відповідь:
![]() ,
,
![]() .
.
ВАРІАНТ 2.
1. При заміні всіх стовпців визначника відповідними за номерами рядками, визначник
а) міняє знак на протилежний, б) приймає нове числове значення,
в) не змінює свого числового значення, г) стає нулем.
2.
Рівняння дотичної до графіка функції
![]() у точці
у точці
![]() має вигляд:
має вигляд:
а)
![]() ,
б)
,
б)
![]() ,
,
в)
![]() ,
г)
,
г)
![]() .
.
3.
Якщо
![]() і якщо
і якщо
![]() ,
то формула заміни змінної має вигляд:
,
то формула заміни змінної має вигляд:
а)
![]() ,
б)
,
б)
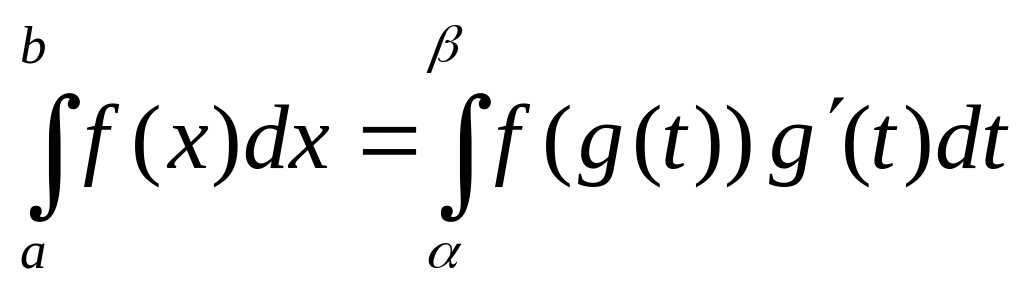 ,
,
в)
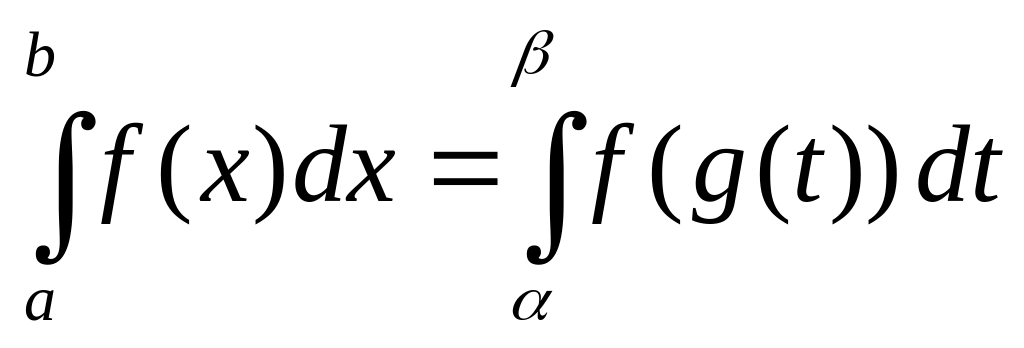 ,
г)
,
г)
![]() .
.
4. Однорідне диференціальне рівняння першого порядку розв'язується шляхом підстановки
а)
![]() ,
б)
,
б)
![]() ,
в)
,
в)
![]() ,
г)
,
г)
![]() .
.
5. Знайти
![]() ,
якщо
,
якщо
![]() ,
,
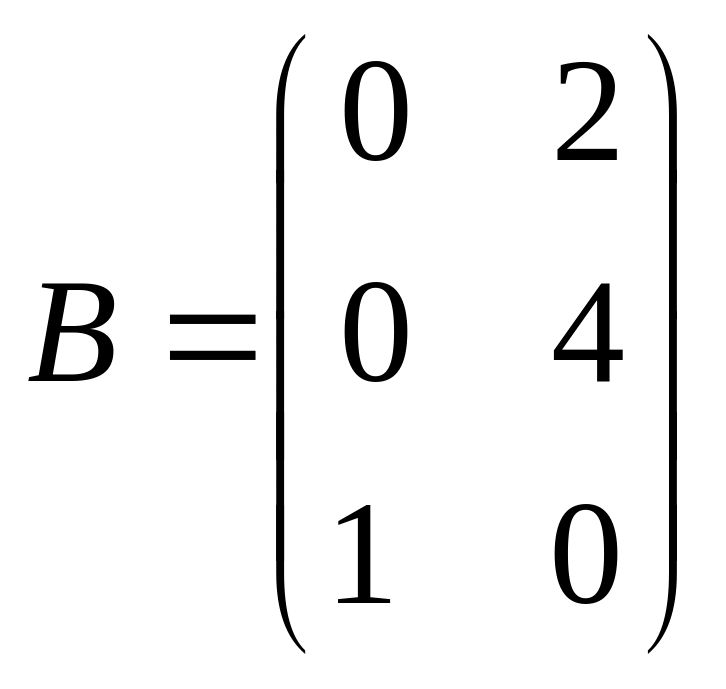 .
.
а)
![]() ,
б)
,
б)
![]() ,
в)
,
в)
![]() ,
г) інша відповідь.
,
г) інша відповідь.
6. Обчислити інтеграл :
а) ![]() ,
б)
,
б) ![]() ,
в)
,
г)
інша відповідь.
,
в)
,
г)
інша відповідь.
7. Знайти
восьмий член ряду
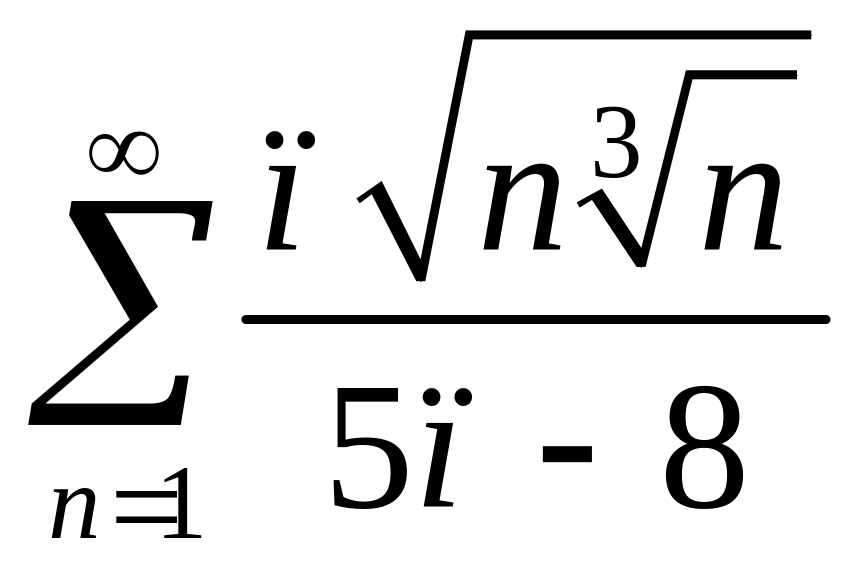 :
:
а)
,
б) 1,
в) ![]() ,
г)
інша відповідь.
,
г)
інша відповідь.
8. Обчислити границю ;
Відповідь:
![]() .
.
9. Розв'язати диференціальне рівняння .
Відповідь:
![]() .
.
ВАРІАНТ 3.
1. Якщо відповідні елементи двох рядків визначника співпадають, то визначник дорівнює
а) подвоєному значенню визначника, що отриманий при викреслюванні відповідних рядків, б) нулю, в) одиниці,
г) сумі добутків елементів цих рядків на їх алгебраїчні доповнення.
2. Величина, обернена нескінченно малій, є
а) величиною, що дорівнює нулю, б) величиною, що прямує до одиниці,
в) нескінченно великою величиною, г) нескінченно малою величиною.
3.
Якщо функції
![]() і
і
![]() диференційовні,
то похідна добутку цих функцій обчислюється
за формулою:
диференційовні,
то похідна добутку цих функцій обчислюється
за формулою:
а)
![]()
![]() ,
б)
,
б)
![]() ,
,
в)
![]() ,
г)
,
г)
![]() .
.
4. Степеневим рядом називається функціональний ряд вигляду:
а)
![]() ,
б)
,
б)
![]() ,
,
в)
![]() ,
,
г)
![]() .
.
5. Якщо
матриця
![]() має розмірність
має розмірність
![]() ,
то матриця
,
то матриця
![]() розмірності
розмірності
а)
,
б)
![]() ,
в)
,
в)
![]() ,
г) інша відповідь.
,
г) інша відповідь.
6. Обчислити границю :
а)
,
б) ![]() ,
в) 0, г)
інша відповідь.
,
в) 0, г)
інша відповідь.
7. Обчислити інтеграл :
а) 2,
б) 0,5,
в) ![]() ,
г)
інша відповідь.
,
г)
інша відповідь.
8. Знайти
похідну функції
![]() .
.
Відповідь:
![]() .
.
9. Розв'язати диференціальне рівняння .
Відповідь:
![]() .
.
ВАРІАНТ 4.
1. Матриця називається квадратною, якщо:
а) всі її елементи не дорівнюють нулю, б) число її рядків не дорівнює числу стовпців,
в) всі її недіагональні елементи дорівнюють нулю,
г) число її рядків дорівнює числу стовпців.
2.
Якщо
![]() ,
то величина
,
то величина
а)
![]() ‑ величина, що дорівнює нулю,
б)
‑ необмежена величина,
‑ величина, що дорівнює нулю,
б)
‑ необмежена величина,
в)
‑ нескінченно мала величина, г) ![]() ‑ нескінченно велика величина.
‑ нескінченно велика величина.
3.
Якщо функції
і
диференційовні
і
![]() ,
то похідна частки цих функцій обчислюється
за формулою:
,
то похідна частки цих функцій обчислюється
за формулою:
а)
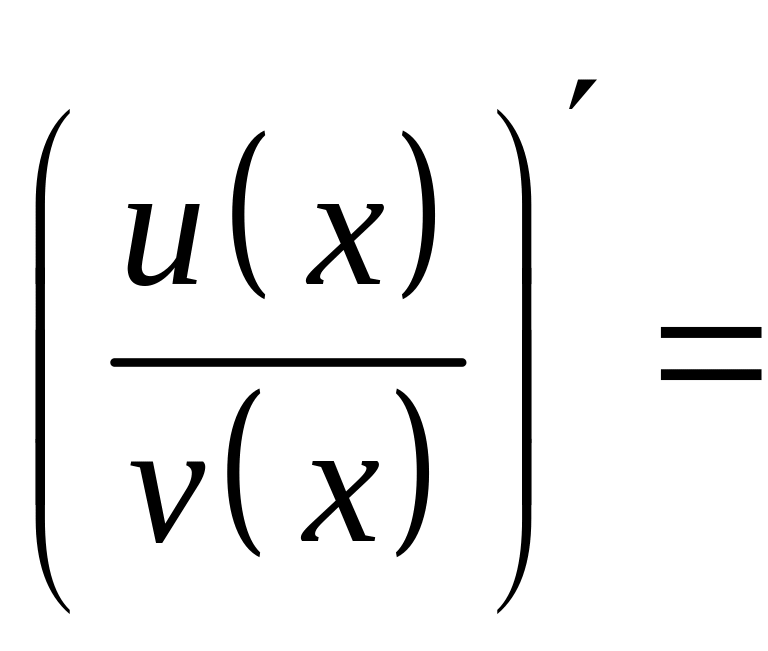
![]() ,
б)
,
б)
![]() ,
,
в)
![]() ,
г)
,
г)
![]() .
.
4.
Формула Ньютона-Лейбніца, якщо
![]() ‑ первісна функції
‑ первісна функції
![]() має вигляд:
має вигляд:
а)
![]() ,
б)
,
б)
![]() ,
,
в)
![]() ,
г)
,
г)
![]() .
.
5. Знайти
визначник матриці
![]() :
:
а)
![]() ,
б)
,
б)
![]() ,
в)
,
в)
![]() ,
г) інша відповідь.
,
г) інша відповідь.
6. Матриця
має розмірність
.
Для того, щоб можна було виконати операцію
додавання
![]() матриця
матриця
![]() повинна мати розмірність
повинна мати розмірність
а) , б) , в) , г) інша відповідь.
7. Обчислити інтеграл :
а) 0,
б) 2,
в) ![]() ,
г)
інша відповідь.
,
г)
інша відповідь.
8. Обчислити
границю
![]() ;
Відповідь:
;
Відповідь:
![]() .
.
9. Розв'язати
диференціальне рівняння
![]() .
Відповідь:
.
Відповідь:
![]() .
.
ВАРІАНТ 5.
1. При множенні матриці на число
а) всі елементи матриці умножаються на це число,
б) елементи одного з будь-яких стовпців умножаються на це число,
в) елементи одного з будь-яких рядків умножаються на це число,
г) матриця стає діагональною.
2. Величина, обернена нескінченно великий, є
а) величиною, що дорівнює нулю, б) величиною, що прямує до одиниці,
в) нескінченно великою величиною, г) нескінченно малою величиною.
3. Похідною другого порядку називається
а) квадрат похідної першого порядку, б) похідна від похідної першого порядку,
в) первісна похідної першого порядку,
г) похідна першого порядку, помножена на два.
4. Формула інтегрування за частинами для визначеного інтеграла має вигляд:
а)
![]() ,
б)
,
б)
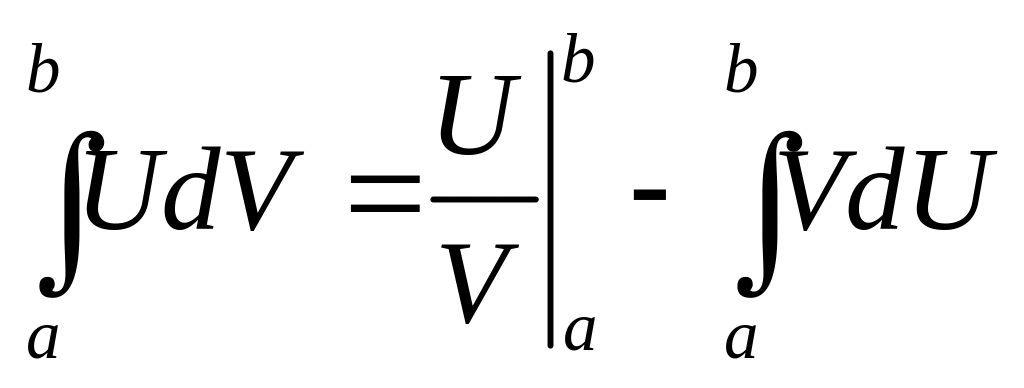 ,
,
в)
![]() ,
г)
,
г)
![]() .
.
5. Знайти
визначник матриці
 :
:
а)
![]() ,
б)
,
б)
![]() ,
в)
,
г) інша відповідь.
,
в)
,
г) інша відповідь.
6. Якщо
матриця
має розмірність
,
а матриця
‑
![]() ,
то розмірність матриці
,
то розмірність матриці
![]()
а)
,
б)
![]() ,
в)
,
в)
![]() ,
г) інша відповідь.
,
г) інша відповідь.
7. Знайти
інтеграл
![]() :
:
а)
![]() ,
б)
,
б) ![]() ,
в)
,
в) ![]() ,
г)
інша відповідь.
,
г)
інша відповідь.
