Пример № 3
Задание: решить транспортную задачу.
Автомобили производятся в трех городах: Питер, Тольятти и Таганрог объемом 8000, 13000 и 10000 штук соответственно.
Их надо перевезти в четыре других города: Киев, Москва, Воронеж, Вена, в количестве 5000, 11000, 11000 и 3500 штук соответственно. Стоимость перевозки авто задана матрицей (таб. 39):
Таблица 39
Стоимость перевозки
1 |
2 |
2 |
0 |
1 |
2 |
0 |
2 |
2 |
1 |
5 |
4 |
Необходимо найти оптимальный план перевозок при минимальной цене, учитывая, что в Киев необходимо поставить ровно 5000 авто, в другие города – не менее запрашиваемого количества. Весь объем произведенных авто необходимо реализовать.
Решение:
Для решения этой задачи применим функцию «Поиск решения». При этом необходимо произвести ряд действий.
Шаг 1. В лист Excel введем таблицу и заполним ее согласно условиям задачи (рис. 77):
85
|
A |
B |
C |
D |
E |
F |
1 |
Города |
Киев |
Москва |
Воронеж |
Вена |
Производство |
2 |
Питер |
1 |
2 |
2 |
0 |
8000 |
3 |
Тольятти |
1 |
2 |
0 |
2 |
13000 |
4 |
Таганрог |
2 |
1 |
5 |
4 |
10000 |
5 |
Потребность |
5000 |
11000 |
11000 |
3500 |
|
6 |
|
|
|
|
|
|
Рис. 77. Исходные данные
Шаг 2. Определим область приложения целевой функции (ЦФ). В данном случае она будет равна по объему диапазону из задания В2:Е4;B9:E11. Для наглядности закрасим эту область в цвет. Тогда Ваш лист примет вид (рис. 78):
Рис. 78. Определение области приложения целевой функции
Шаг. 3. Составим целевую функцию. В данной задаче она будет равна сумме произведений ячеек В2:Е4 на ячейки В9:Е11, и будет выглядеть следующим образом: =СУММПРОИЗВ(B2:E4;B9:E11). То есть в диапазоне ячеек В9:Е11 компьютер должен посчитать график перевозок. Внесем эту формулу в ячейку F15 (рис. 79).
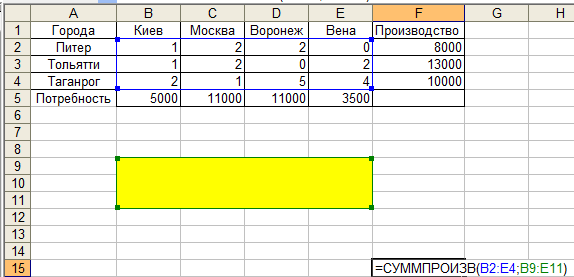
Р
86
Шаг 4. Далее необходимо задать ограничения, взятые из условия задачи. Из условия следует, что первый пункт (Киев) должен быть удовлетворен полностью, то есть в него надо отгрузить 5000 автомобилей. В остальные пункты (Москва, Воронеж, Вена) – не менее заданного количества. Для этого в ячейки В12:Е12 внесем формулы, суммирующие данные из диапазона В9:Е11 (рис. 80).
Также необходимо ограничить наши запасы автомобилей. Для этого в ячейки F9:F11 внесем формулы, суммирующие данные из диапазона В9:Е11 (рис. 81).
|
A |
B |
C |
D |
E |
F |
8 |
|
|
|
|
|
|
9 |
|
|
|
|
|
=СУММ(B9:E9) |
10 |
|
|
|
|
|
=СУММ(B10:E10) |
11 |
|
|
|
|
|
=СУММ(B11:E11) |
|
|
=СУММ(B9:B11) |
=СУММ(C9:C11) |
=СУММ(D9:D11) |
=СУММ(E9:E11) |
|
|
|
|
|
|
|
|
Рис. 80. Введение формул для ограничений
Шаг 5. В результате перечисленных (в шагах 1-4) действий лист Excel должен принять следующий вид (рис. 81):
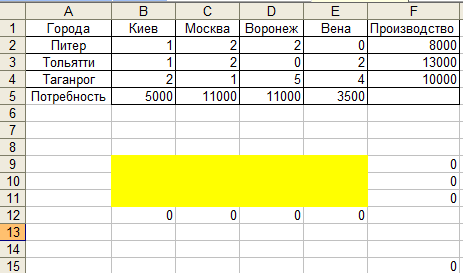
Рис. 81. Итоговая таблица
Шаг 6. Воспользуемся функцией «Поиск решения». Для этого выделим курсором ячейку с целевой функцией (F15), и зайдем в меню «Сервис»-«Поиск решения». Заполним диалоговое окно «Поиск решения»:
- в строке «установить целевую ячейку» введем $F$15;
- в строке «равной» установим «минимальному значению»;
- в поле «Изменяя ячейки» введем диапазон ячеек $B$9:$E$11.
Должно получиться следующее окно (рис. 82).
87
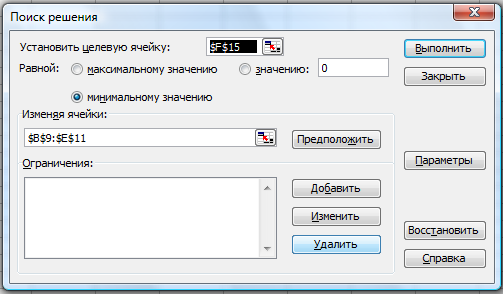
Рис. 82. Диалоговое окно «Поиск решения»
После произведенных действий, введем ограничения, нажав клавишу «Добавить». После этого появится окно «Добавление ограничения» (рис. 83).
Рис. 83. Окно «Добавление ограничения»
В окно «Добавление ограничения» (рис. 83) ведем первое ограничение (рис. 84). Данные рисунка 84 означают, что компьютер должен считать все автомобили в целых числах, то есть без половин, четвертей и пр.
Рис. 84. Окно «Добавление ограничения»
После произведенных действий введем второе ограничение, нажав кнопку «Добавить» окна «Добавление ограничения» (рис. 85). Данные рисунка 85 означают, что все полученные значения должны быть больше или равны нулю (то есть быть неотрицательными).
88
Рис. 85. Окно «Добавление ограничения»
Введем третье ограничение, нажав кнопку «Добавить» окна «Добавление ограничения» (рис. 86). Данные рисунка 86 означают, что в Киев надо привезти ровно 5000 автомобилей.
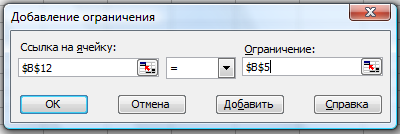
Рис. 86. Окно «Добавление ограничения»
Введем четвертое ограничение, нажав кнопку «Добавить» окна «Добавление ограничения» (рис. 87). Данные рисунка 87 означают, что в остальные города можно привезти автомобилей больше, чем заказано.
Рис. 87. Окно «Добавление ограничения»
Введем пятое ограничение, нажав кнопку «Добавить» окна «Добавление ограничения» (рис. 88). Данные рисунка 88 означают, что мы не можем перевезти больше автомобилей, чем их изготовлено.
Рис. 88. Окно «Добавление ограничения»
89
Таким образом, окно «Поиск решения» будет иметь следующий вид (рис. 89):
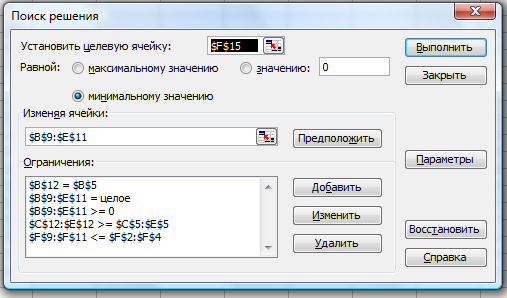
Рис. 89. Диалоговое окно «Поиск решения»
Шаг 7. Нажав кнопку «Выполнить», мы получим решение данной задачи (рис. 90):
Рис. 90. Окно «Результаты поиска решения»
Нажав кнопку «ОК», мы получим лист Excel следующего вида (рис.91):
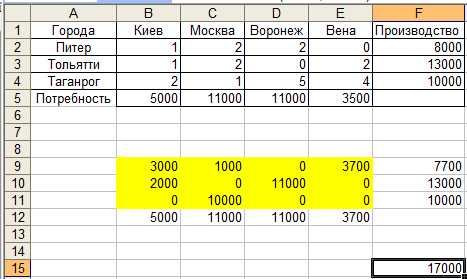
Р
90
Вывод: в город Киев привезено 5000 автомобилей, в город Москва – 11000 автомобилей, в город Воронеж – 11000 автомобилей, в город Вена – 3700 автомобилей.
Обратите внимание, что не произошло превышение запасов автомобилей находящихся на складе (при затратах равных 17000). Задача решена.