Любой компьютер содержит:
Арифметико-логическое устройство (АЛУ),
Запоминающее устройство (память),
Управляющее устройство
Устройство ввода-вывода информации (УВВ) и имеет программу, хранимую в его памяти (архитектура Джона фон Неймана).
Системный блок включает в себя: процессор, оперативное запоминающее устройство (ОЗУ) (размещены на материнской плате), накопители на гибких и жестких магнитных дисках, источник питания и др.
Устройства ввода информации: клавиатура, мышь, накопители на гибких магнитных дисках, модем, компьютерная сеть, сканер, световое перо, джойстик, трекбол, микрофон, дисковод CD-ROM.
Устройства вывода информации: монитор, принтер, плоттер, накопители на гибких магнитных дисках, звуковые колонки, встроенный динамик, стриммер, модем, компьютерная сеть.
Процессор: предназначен для вычислений, обработки информации и управления работой компьютера; ОЗУ, накопители на гибких и жестких магнитных дисках — для хранения информации. Процессоры характеризуются быстродействием и разрядностью Разрядность процессоров составляет 8, 16, 32, 64 бит.
Память: компьютера бывает внутренней и внешней. К внутренней памяти относится постоянное ЗУ (ПЗУ-BIOS или CMOS Setup), ОЗУ, КЭШ, видеопамять. К устройствам внешней памяти относятся накопители на жестком и гибком магнитных дисках (HDD и FDD), CD-ROM, магнитооптический диск и стриммер. ОЗУ используется процессором для кратковременного хранения информации во время работы компьютера.
КЭШ-память — это сверхоперативная сверхскоростная промежуточная память. КЭШ устраняет простои процессора, Наличие КЭШ в 256 Кб может увеличить производительность ПК на 20%. Размер КЭШ-памяти составляет от 64 Кб до 512 Кб.
НАКОПИТЕЛИ на гибких (FDD) и жестких (HDD) магнитных дисках служат для постоянного хранения информации.
КЛАВИАТУРА предназначена для ручного ввода информации в компьютер. Она содержит клавиши латинских и русских букв, цифр, различных знаков и специальные функциональные клавиши. Клавиатура компьютера состоит из 6 групп клавиш:
Буквенно-цифровые;
Управляющие;
Функциональные;
Цифровая клавиатура;
Управления курсором;
Световые индикаторы функций.
МОНИТОР (дисплей) предназначен для отображения информации на экране. Существуют текстовый и графический режимы дисплея.
Видеопамять — это специальная оперативная память, в которой формируется графическое изображение. К персональному компьютеру могут подключаться и другие дополнительные устройства (мышь, принтер, сканер и др.). Подключение производится через ПОРТЫ — специальные разъемы на задней панели, бывают параллельные и последовательные.
ПРИНТЕРЫ — для распечатки текста и графических изображений. Принтеры бывают матричные, струйные и лазерные.
МЫШЬ — манипулятор для управления.
3. Экономический эффект предполагает какой-либо полезный результат, выраженный в стоимостной оценке. Обычно в качестве полезного результата выступает прибыль или экономия затрат и ресурсов.
Все показатели, рынка можно разделить:
1. на оценочные, характеризующие достигнутый или возможный уровень развития или результатов той или иной деятельности;
2. затратные, отражающие уровень затрат по осуществлению различных видов деятельности.
В зависимости от цели анализа показатели могут выражаться в форме абсолютных, относительных и средних величин.
Абсолютные показатели бывают стоимостными и натуральными. В условиях рыночных отношений первостепенное значение придается стоимостным показателям, что обусловлено сущностью товарно-денежных отношений. Абсолютные показатели отражают уровень развития предприятия, достигнутый за определенный период времени
натуральные показатели объемов производства (штуки, метры, тонны и т.д.). Их используют при анализе объемов производства по отдельным видам однородной продукции.
Относительные показатели определяются как отношения абсолютных показателей, характеризующие долю одного показателя в другом, или как отношения разнородных показателей.К этим показателям относятся: прибыль на единицу стоимости основных средств, издержек или уставного фонда; производительность.
При́быль — превышение в денежном выражении доходов (выручки от реализации товаров и услуг) над затратами на производство или приобретение и сбыт этих товаров и услуг
Рентабельность это показатель, характеризующий уровень доходности предприятия, выраженный в процентах. Рентабельность осуществляется как отношение прибыли к затратам.
Рентабельность продукции (норма прибыли) – отношение общей суммы прибыли к издержкам производства и реализации продукции, т.е. относительная величина прибыли, приходящейся на 1 руб. текущих затрат.
Рентабельность производства (Ро) показывает отношение общей суммы прибыли к среднегодовой стоимости основных и нормируемых оборотных средств, т.е. величину прибыли в расчете на 1 руб. производственных фондов.
Также часто используются показатели рентабельности активов (капитала), рентабельности чистых активов, рентабельности собственного капитала и рентабельности реализации.
Билет 5 1. а) Lim[n->] y[n]=b. Опр-е: число b наз-ся пределом последовательности y[1],y[2],…,y[n],…, если абсолютная величина разности y[n]-b, начиная с некоторого номера N, остается меньшей любого заранее данного полож-го числа : |y[n]-b|<, при n>=N (N зависит от ).
lim[x->a] f(x)=b число b наз-ся пределом функции f(x) при x->a, если по мере того как x приближается к a будь то с права или слева, - значение f(x) неограниченно приближается к b. f(x) в точке a м.б неопр-на. Опр-е: число b есть предел ф-ии f(x) при x->a, если величина |f(x)-b| сколь угодно мала, при достаточной малости величины |x-a|.
Свойства пределов.
Предел алгебраической суммы равен алгебраической сумме пределов, т.е.
Предел произведения равен произведению пределов:
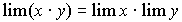
Постоянную величину можно выносить за знак предела:
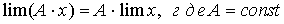
Предел частного равен частному пределов делимого и делителя, если предел делителя не равен нулю:
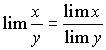
Предел целой положительной степени переменной величины равен той же степени предела той же переменной:
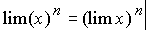
Виды неопределенности и некоторые способы их раскрытия.
Часто
при решении примеров на нахождение
пределов функций получаются выражения
вида:
Выражения
такого вида называются неопределенностями,
а процесс нахождения предела таких
выражений — раскрытием неопределенности.
Существуют стандартные методы для
раскрытия неопределенностей каждого
вида. Поясним это на примерах.
Решение примеров на нахождение пределов функций начинается с выяснения вопроса: есть неопределенность или ее нет. Если ее нет, то в функцию вместо переменной х подставляют предел, к которому х стремится, производят соответствующие алгебраические действия, результат которых и будет решением примера.
Например,
найти
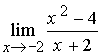
Решение:
Подставив х = –2 в выражение
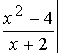получим неопределенность вида
Раскрытие
неопределенности достигается разложением
числителя на сомножители (как разность
квадратов): (х – 2)(х + 2), с последующим
сокращением на х – 2. Сомножитель (х –
2), содержащий неопределенность, уходит,
и мы можем теперь подставить вместо х
его предел и получить решение примера,
т.е.
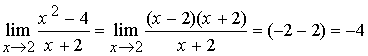
2. а) В информатике, как правило, измерению подвергается информация, представленная дискретным сигналом. При этом различают следующие подходы:
-Структурная мера: измеряет количество информации простым подсчетом информационных элементов, составляющих сообщение. Применяется для оценки возможностей запоминающих устройств, объемов передаваемых сообщений, инструментов кодирования без учета статистических характеристик их эксплуатации.
-Статистическая мера: учитывает вероятность появления сообщений: более информативным считается то сообщение, которое менее вероятно, т.е. менее всего ожидалось. Применяется при оценке значимости получаемой информации.
-Семантическая мера: учитывает целесообразность и полезность информации. Применяется при оценке эффективности получаемой информации и ее соответствия реальности.
Единица количества информации - величина информации, которой по определению присвоено значение, равное единице.
Единицы измерения информации служат для измерения объёма информации.
Объёмы информации можно представлять как логарифм количества состояний. Соответствующая ему единица — бит — является основой исчисления информации в цифровой технике.
3. Счет – способ группировки инф-и о состоянии и измерении БУ с целью текущего контроля.
Активные – предназначены для отражения состояния и движения ХС (учитывается то, что есть у пп)
Пассивные – пред для отраж состояния и движения источников ХС.
Синтетический учет – пред для отраж ХС и их источников в обобщенном виже. Особенность отражения объектов только в денеж выражении.
Аналитический учет – пред для конкретизации данных синтет счетов. Это счета на кот-х отраж детальные данные по каждому виду имущества обязательств и процессов. Открывается к определенному синт-му счету.
Уровни счетов: 1.Синтет счета; 2. Суб счета (промежуточное учет звено м/у А и С счетами); 3. Аналит счета.
План счетов – систематизирующий перечень С счетов и субсчетов, в основе которого исп-я классификация счетов по их Э содержанию. Является единым и обязательным для всех пп, кроме банков и бюждет орган-й.
Забалансовые счета – счета, на котор-х отражается ТМЦ, временно находящиеся на пп, но не принадлежащие ему. Они не вкл в валюту баланса (итог баланса). Не применяется метод 2й записи.
Билет 6 1.а) Основной целью экономики является рациональное функционирование хозяйствующих субъектов, т. е. оптимальная деятельность при ограниченных ресурсах. Одним из основных научных направлений в этой области является линейное программирование, методы которого активно используются в прогнозных расчетах, планировании и организации производственных процессов, а также в финансовой сфере.
Опр.: Линейное программирование — это область математического программирования, являющегося разделом математики, в котором изучаются методы исследования и отыскания экстремальных (наибольших и наименьших) значений некоторой линейной функции,на аргументы которой наложены линейные ограничения. Такая линейная функция называется целевой, а набор количественных соотношений между переменными, выражающих определенные требования экономической задачи в виде уравнений или неравенств, называется системой ограничений. Слово «программирование» введено в связи с тем, что неизвестные переменные, которые находятся в процессе решения задачи, обычно определяют программу, или план работы некоторого экономического субъекта.
Определение 2. Совокупность соотношений, содержащих целевую
функцию и ограничения на ее аргументы, называется математической моделью экономической задачи оптимизации.
Постановка задачи коммерческой деятельности может быть представлена в виде математической модели линейного программирования, если целевая функция может быть представлена в виде линейной формы, а связь с ограниченными ресурсами описать посредством линейных уравнений или неравенств. Кроме того, вводится дополнительное ограничение – значения переменных должны быть неотрицательны, поскольку они представляют такие величины, как товарооборот, время работы, затраты и другие экономические показатели.
В общем виде математическая модель задачи линейного программирования (ЗЛП) записывается как
L( ) = c1x1 + с2х2 + ... + CjXj + ... + CnXn max(min)
при ограничениях
где неизвестные; постоянные заданные величины.Наиболее распространенная интерпретация сформулированной задачи состоит в следующем: имеется п ресурсов при некоторых т ограничениях; нужно определить объемы этих ресурсов xj, при которых целевая функция будет достигать максимума (минимума), т. е. найти оптимальное распределение ограниченных ресурсов. При этом возникают также и ограничения, которые называются естественными:
Следует особо отметить, что экстремум целевой функции ищется на допустимом множестве решений, определяемом системой ограничений. При этом все или некоторые уравнения системы ограничений могут быть записаны также в виде неравенств.
Математическая модель в более краткой записи имеет вид
L( )= max(min)
при ограничениях
Xj 0, i =, j = .
Для составления математической модели ЗЛП необходимо выполнить следующие этапы:
• обозначить переменные;
• составить целевую функцию в соответствии с целью задачи;
• записать систему ограничений с учетом имеющихся в условии задачи показателей
Если все ограничения задачи заданы уравнениями, а переменные Xj неотрицательные, то модель такого вида называется канонической. Если хотя бы одно ограничение является неравенством, то модель называется неканонической. Далее мы укажем наиболее распространенные методы решения задач линейного программирования.