Билет 1

1. а) Ма́трица — математический объект, записываемый в виде прямоугольной таблицы элементов кольца или поля (например, целых или комплексных чисел), которая представляет собой совокупность строк и столбцов, на пересечении которых находятся её элементы. Количество строк и столбцов матрицы задают размер матрицы.

Матрицей размерности m x n называется прямоугольная таблица m x n чисел a _ij , i=1,..., m, j=1,..., n:

расположенных в m строках и n столбцах. Матрица называется квадратной, если m=n (n - порядок матрицы).

Линейные матричные операции

По определению, чтобы умножить матрицу на число, нужно умножить на это число все элементы матрицы.

Суммой двух матриц одинаковой размерности, называется матрица той же размерности, каждый элемент которой равен сумме соответствующих элементов слагаемых.

П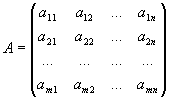 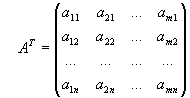роизведение матриц определяется следующим образом. Пусть заданы две матрицы A и B, причем число столбцов первой из них равно числу строк второй. Если то произведением матриц A и B, называется матрица, элементы которой вычисляются по формуле c _ij =a _i1 b _1j + a _i2 b _2j + ... +a _in b _nj , i=1, ..., m, j=1, ..., k.

Произведение матриц A и B обозначается AB, т.е. C=AB.

Произведение матриц, вообще говоря, зависит от порядка сомножителей. Если AB=BA, то матрицы A и B называются перестановочными.

Для квадратных матриц определена единичная матрица - квадратная матрица, все диагональные элементы которой единицы, а остальные - нули:

Единичная матрица чаще всего обозначается буквой E или E n, где n - порядок матрицы. Непосредственным вычислением легко проверить основное свойство единичной матрицы: AE=EA=A.

Скалярной матрицей называется диагональная матрица с одинаковыми числами на главной диагонали; единичная матрица - частный случай скалярной матрицы. Умножение матрицы на матрицы специального вида

Для квадратных матриц определена операция возведения в целую неотрицательную степень: A ⁰ =E, A ¹ =A, A ² =AA, ..., A ⁿ =A ^n-1 A, ....

 Для прямоугольных матриц определена операция транспонирования. Рассмотрим произвольную прямоугольную матрицу A. Матрица, получающаяся из матрицы A заменой строк столбцами, называется транспонированной по отношению к матрице и обозначается A ^T:

Верны соотношения: (A^T )^T =A; (A+B)^T=A^T +B^T ; (AB)^T =B^T A^T.

Квадратная матрица A, для которой A^T =A, называется симметричной. Элементы такой матрицы, расположенные симметрично относительно главной диагонали, равны.

Квадратная матрица A называется обратимой, если существует такая матрица X, что AX=XA=E. Матрица X называется обратной к матрице A и обозначается A ^-1, т.е. A A ^-1 =A ^-1A=E.. Известно, что если матрица A невырождена (т.е ее определитель отличен от нуля), то у нее существует обратная матрица A ^-1.Верно соотношение: (A^-1)^T =(A^T ) ^-1.

Квадратная матрица U, для к-ой U ^-1 =U ^T,, называется ортогональной матрицей.

Свойства ортогональной матрицы:

Модуль определителя ортогональной матрицы равен единице.

Сумма квадратов элементов любого столбца ортогональной матрицы равна единице.

Сумма произведений элементов любого столбца ортогональной матрицы на соответствующие элементы другого столбца равна нулю. Такими же свойствами обладают строки ортогональной матрицы.

Определитель

Пусть A квадратная матрица порядка n, n>1. Определителем квадратной матрицы A порядка n называется число

det A=

где M₁ ^<j> - определитель квадратной матрицы порядка n -1, полученной из матрицы A вычеркиванием первой строки и j -го столбца, называемый минором элемента a_1j .

Формула

det A = 

называется формулой вычисления определителя разложением по первой строке. Число (-1) ^j+1 M₁ ^<j> называется алгебраическим дополнением элемента a_1j. Пусть M_i ^<j> - определитель квадратной матрицы порядка n-1, полученной из матрицы A вычеркиванием i-й строки и j-го столбца (минор элемента a_ij ). Число (-1) ^j+i M_i ^<j> называется алгебраическим дополнением элемента aij матрицы A. Справедливы формулы вычисления определителя квадратной матрицы A разложением по i-й строке и разложением по j-му столбцу:

d et A=

для i=1,2,...,n, j=1,2,...,n.

Для квадратной матрицы второго порядка формула вычисления определителя упрощается:

d et 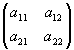= = 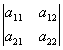a₁₁ a₂₂ - a₁₂ a₂₁,

поскольку, например, в формуле разложения определителя по 1-ой строке  M1 < 1> =a22 , M1 < 2> =a21.

Для квадратной матрицы третьего порядка формула вычисления определителя разложением по 1-ой строке имеет вид:

= - + .

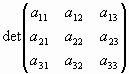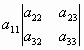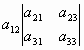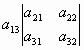2. а) Все современные дисковые операционные системы обеспечивают создание файловой структуры, предназначенной для хранения данных на дисках и обеспечения доступа к ним. Принцип организации файловой структуры – табличный.

Данные, о том, в каком месте диска записан тот или иной файл, хранятся в системной области диска в специальных таблицах размещения файлов (FAT-таблицах). К FAT-таблице предъявляются очень высокие требования по её надёжности, поскольку нарушение FAT-таблицы приводит к нарушению доступа к данным, записанным на диске.

Наименьшей физической единицей хранения данных является сектор.

Под управлением операционной системы осуществляются следующие функции обслуживания файловой структуры:

создание файлов и присвоение им имён;

создание каталогов (папок) и присвоение им имён;

копирование и перемещение файлов между дисками и между каталогами (папками) одного диска;

удаление файлов и каталогов (папок);

навигация по файловой структуре с целью доступа к заданному файлу, каталогу (папке);

управление атрибутами файлов.

Файл – это именованная последовательность байтов произвольной длины.

Операции с файлами: Создание папок, Создание файлов, Переименование папок и файлов, Перемещение и копирование папок и файлов, Удаление папок и файлов, Восстановление удаленных папок и файлов, Действия с группами папок и файлов, Поиск папок и файлов. Архивирование файлов

3. Государственный кредит – это совокупность экономических отношений, возникающих между государством как заемщиком (или займодателем) денежных средств и физическими (юридическими) лицами, иностранными правительствами в процессе формирования и использования общегосударственного фонда денежных ресурсов.

Государственный кредит отличается от банковского. Он, как правило, используется для покрытия дефицита государственного бюджета. Источником его возврата и уплаты процентов являются доходы бюджета, а не прибыль от выгодно размещенного кредита.

Его источником являются свободные средства населения, предприятий и организаций.

Существование государственного кредита приводит к появлению государственного долга. Сумма его состоит из сумм всех выпущенных и непогашенных долговых обязательств государства (как внутренних, так и внешних), включая выданные гарантии по кредитам, которые предоставляются иностранным заемщикам, местным органам власти, государственным предприятиям.

Государственный долг имеет экономически обоснованные границы. Величина долга характеризует состояние экономики и финансов государства, эффективность функционирования его правительственных структур. Поскольку источником покрытия государственного долга являются доходы бюджета, то есть налоги, можно утверждать, что величина долга – это взятые авансом у населения налоги.

В большинстве стран мира величина государственного долга регулируется законодательно. Государственный внутренний долг гарантируется всем имуществом, которое находится в общегосударственной собственности. Государственный долг подразделяется на капитальный и текущий. Капитальный государственный долг представляет всю сумму выпущенных и непогашенных долговых обязательств государства, включая начисленные проценты, которые должны быть выплачены по этим обязательствам. Текущий государственный долг составляет расходы по выплате доходов кредиторам по всем долговым обязательствам государства и по погашению обязательств, срок оплаты которых наступил.

Билет 2 1.а) Первообра́зной или примити́вной функцией (иногда называют также антипроизводной) данной функции f называют такую F, производная которой (на всей области определения) равна f, то есть F′= f. Вычисление первообразной заключается в нахождении неопределённого интеграла, а сам процесс называется интегрированием.

Т ак, например, функция является первообразной .

Т ак как производная константы равна нулю, будет иметь бесконечное количество первообразных; таких как или … и т. д.; таким образом семейство первообразных функции x² можно обозначить как F(x) = x³ / 3 + C, где C — любое число. Графики таких первообразных смещены вертикально относительно друг друга, и их положение зависит от значения C.

Первообразные важны тем, что позволяют вычислять интегралы. Если F — первообразная интегрируемой функции f, то:

Это соотношение называется формулой Ньютона — Лейбница.

Благодаря этой связи множество первообразных данной функции f называют неопределённым интегралом (общим интегралом) f и записывают в виде интеграла без указания пределов:

Е сли F — первообразная f, и функция f определена на каком-либо интервале, тогда каждая последующая первообразная G отличается от F на константу: всегда существует число C, такое что G(x) = F(x) + C для всех x. Число C называют постоянной интегрирования.

Каждая непрерывная функция f имеет первообразную F, одна из которых представляется в виде интеграла от f с переменным верхним пределом:

Также существуют не непрерывные (разрывные) функции, которые имеют первообразную. Например,

с f(0) = 0 не непрерывна при x = 0, но имеет первообразную с F(0) = 0.

Некоторые первообразные, даже несмотря на то, что они существуют, не могут быть выражены через элементарные функции (такие как многочлены, экспоненциальные функции, логарифмы, тригонометрические функции, обратные тригонометрические функции и их комбинации). Например:

В курсе микроэкономики часто рассматривают так называемы предельные величины, т.е. для данной величины, представляемой некоторой функцией у =f(x), рассматривают ее производную f'x. Например, если дана функция издержек С в зависимости от объема q выпускаемого товара С = С(q), то предельные издержки будут задаваться производной этой функции МС = С'(q). Ее экономический смысл - это издержки на производство дополнительной единицы выпускаемого товара. Поэтому часто приходится находить функцию издержек по данной функции предельных издержек.

2.а) Модель - это некий новый объект, который отражает существенные особенности изучаемого объекта, явления или процесса.

Признаки классификаций моделей:

1) по области использования;

Учебные модели – используются при обучении;

Опытные – это уменьшенные или увеличенные копии проектируемого объекта. Используют для исследования и прогнозирования его будущих характеристик

Научно - технические - создаются для исследования процессов и явлений

Игровые – репетиция поведения объекта в различных условиях

Имитационные – отражение реальности в той или иной степени (это метод проб и ошибок)

2) по фактору времени;

Статические – модели, описывающие состояние системы в определенный момент времени (единовременный срез информации по данному объекту). Примеры моделей: классификация животных…., строение молекул, список посаженных деревьев, отчет об обследовании состояния зубов в школе.

Динамические – модели, описывающие процессы изменения и развития системы (изменения объекта во времени). Примеры: описание движения тел, развития организмов, процесс химических реакций.

3) по отрасли знаний;

это классификация по отрасли деятельности человека: Математические, биологические, химические, социальные, экономические, исторические.

4) по форме представления

Материальные – это предметные (физические) модели.

Абстрактные (нематериальные) – не имеют реального воплощения.

По степени формализации информационные модели бывают образно-знаковые и знаковые.

Образно-знаковые модели :Геометрические (рисунок, пиктограмма, чертеж, карта, план, объемное изображение)Структурные (таблица, граф, схема, диаграмма)Словесные (описание естественными языками)Алгоритмические (нумерованный список, пошаговое перечисление, блок-схема)

Знаковые модели: Математические – представлены матем.формулами, отображающими связь параметров; Специальные – представлены на спец. языках (ноты, хим.формулы);

Алгоритмические – программы; Признаки классификаций моделей:Классификация моделей по области использования

Формы: Все модели можно разбить на два больших класса: модели предметные (материальные) и модели знаковые (информационные). Предметные модели воспроизводят геометрические, физические и другие свойства объектов в материальной форме. В процессе обучения широко используются такие модели: глобус (география), муляжи (биология), модели кристаллических решеток (химия) и др.

Модели информационные представляют объекты и процессы в форме рисунков, схем, чертежей, таблиц, формул, текстов и т. д. В школе часто применяются такие модели: рисунок цветка (ботаника), карта (география), формула (физика), блок-схема алгоритма (информатика), периодическая система элементов Д. И. Менделеева (химия), уравнение (математика) и т. д.

Никакая модель не может заменить сам объект. Но при решении конкретной задачи, когда нас интересует определенное свойство изучаемого объекта, модель оказывается полезным, а подчас и единственным инструментом исследования.

3. Налоговой контроль – контроль за функциями нс, который заключается в контроле за обеспечиванием своевременности и уплаты нп налогов в их полном объеме. Правильно организованный нк имеет 2 стороны:

- Широкие полномочия НО

- Уважение к нп и не причинение ему вреда.

Этапы нк:

1. Постановка на учет в НО все пп (ю.ф.л.) подлежащие обязательной постановке на учет в ФНС. Постановка на учет осуществляется по месту нахождения нп. В НО нк предоставляют ИНН.

2. Проведение налоговых проверок. Виды проверок:

Камеральные – форма текущего контроля, проводимая по месту нахождения но

Выездные – форма текущего контроля, проводимая по месту нахождения НП.

Финансовые санкции - мера гос. принуждения, применяемая к н/п в бесспорном порядке и выражающаяся в виде недоимок, штрафов, пени и т.д.

Виды санкции:

- правовостанновительные (компенсационные)

• пени

• недоимка

- карательные

• административная (штраф)

• уголовная (лишение свободы)

Билет 3

1.а) Основной целью экономики является рациональное функционирование хозяйствующих субъектов, т. е. оптимальная деятельность при ограниченных ресурсах. Одним из основных научных направлений в этой области является линейное программирование, методы которого активно используются в прогнозных расчетах, планировании и организации производственных процессов, а также в финансовой сфере.

Опр.: Линейное программирование — это область математического программирования, являющегося разделом математики, в котором изучаются методы исследования и отыскания экстремальных (наибольших и наименьших) значений некоторой линейной функции,на аргументы которой наложены линейные ограничения. Такая линейная функция называется целевой, а набор количественных соотношений между переменными, выражающих определенные требования экономической задачи в виде уравнений или неравенств, называется системой ограничений. Слово «программирование» введено в связи с тем, что неизвестные переменные, которые находятся в процессе решения задачи, обычно определяют программу, или план работы некоторого экономического субъекта.

Определение 2. Совокупность соотношений, содержащих целевую

функцию и ограничения на ее аргументы, называется математической моделью экономической задачи оптимизации.

Постановка задачи коммерческой деятельности может быть представлена в виде математической модели линейного программирования, если целевая функция может быть представлена в виде линейной формы, а связь с ограниченными ресурсами описать посредством линейных уравнений или неравенств. Кроме того, вводится дополнительное ограничение – значения переменных должны быть неотрицательны, поскольку они представляют такие величины, как товарооборот, время работы, затраты и другие экономические показатели.

В общем виде математическая модель задачи линейного программирования (ЗЛП) записывается как

L( ) = c1x1 + с2х2 + ... + CjXj + ... + CnXn max(min)

при ограничениях

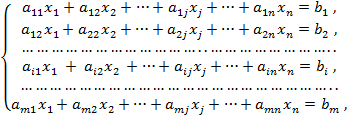
где неизвестные; постоянные заданные величины.Наиболее распространенная интерпретация сформулированной задачи состоит в следующем: имеется п ресурсов при некоторых т ограничениях; нужно определить объемы этих ресурсов xj, при которых целевая функция будет достигать максимума (минимума), т. е. найти оптимальное распределение ограниченных ресурсов. При этом возникают также и ограничения, которые называются естественными:

Следует особо отметить, что экстремум целевой функции ищется на допустимом множестве решений, определяемом системой ограничений. При этом все или некоторые уравнения системы ограничений могут быть записаны также в виде неравенств.

Математическая модель в более краткой записи имеет вид

L( )= max(min)

при ограничениях

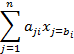
Xj 0, i =, j = .

Для составления математической модели ЗЛП необходимо выполнить следующие этапы:

• обозначить переменные;

• составить целевую функцию в соответствии с целью задачи;

• записать систему ограничений с учетом имеющихся в условии задачи показателей

Если все ограничения задачи заданы уравнениями, а переменные Xj неотрицательные, то модель такого вида называется канонической. Если хотя бы одно ограничение является неравенством, то модель называется неканонической. Далее мы укажем наиболее распространенные методы решения задач линейного программирования.

Графический способ решения злп.

Геометрическая интерпретация экономических задач дает возможность наглядно представить, их структуру, выявить особенности и открывает пути исследования бо­лее сложных свойств. ЗЛП с двумя переменными всегда можно решить графически. Однако уже в трехмерном пространстве такое решение усложняется, а в простран­ствах, размерность которых больше трех, графическое решение, вообще говоря, невозможно. Случай двух переменных не имеет особого практиче­ского значения, однако его рассмотрение проясняет свой­ства ОЗЛП, приводит к идее ее решения, делает геомет­рически наглядными способы решения и пути их практи­ческой реализации.

Пусть дана задача

(1)

(2)

(3)

Дадим геометрическую интерпретацию элементов этой задачи. Каждое из ограничений (2), (3) задает на плоскости некоторую полуплоскость. Полу­плоскость — выпуклое множество. Но пересечение любого числа выпуклых множеств является выпуклым множест­вом. Отсюда следует, что область допустимых решений задачи (1) — (3) есть выпуклое множество.

Перейдем к геометрической интерпретации целевой функции. Пусть область допустимых решений ЗЛП — не­пустое множество, например многоугольник .

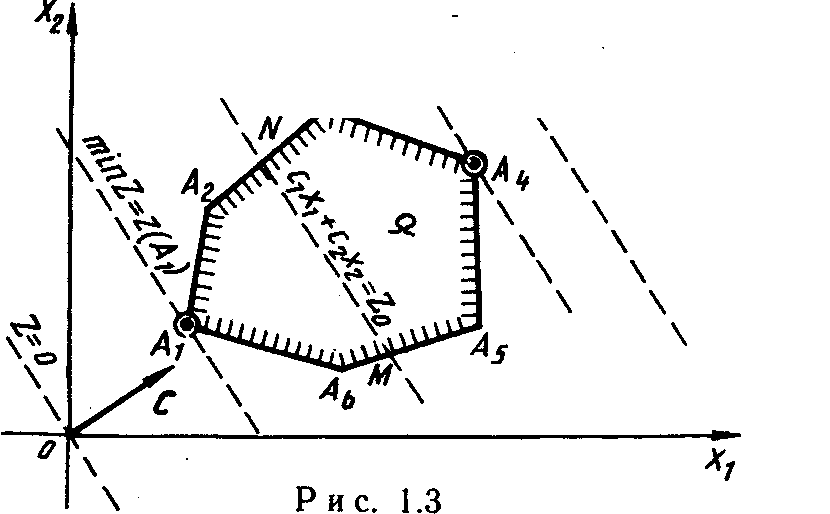
Выберем произвольное значение целевой функ­ции . Получим . Это уравнение пря­мой линии. В точках прямой NМ целевая функция сохра­няет одно и то же постоянное значение . Считая в ра­венстве (11) параметром, получим уравнение семей­ства параллельных прямых, называемых линиями уровня целевой функции (линиями постоянного значения).

Найдём частные производные целевой функции по и

(4)

(5)

Частная производная (4) ((5)) функции пока­зывает скорость ее возрастания вдоль данной оси. Следо­вательно, и — скорости возрастания соответст­венно вдоль осей и . Вектор называ­ется градиентом функции. Он показывает направление наискорейшего возрастания целевой функции:

Вектор — указывает направление наискорейшего убывания целевой функции. Его называют антигра­диентом.

Вектор перпендикулярен к прямым семейства

Из геометрической интерпретации элементов ЗЛП вы­текает следующий порядок ее графического решения.

1. С учетом системы ограничений строим область до­пустимых решений

2. Строим вектор наискорейшего возра­стания целевой функции — вектор градиентного направ­ления.

3. Проводим произвольную линию уровня

4. При решении задачи на максимум перемещаем ли­нию уровня в направлении вектора так, чтобы она касалась области допустимых решений в ее крайнем по­ложении (крайней точке). В случае решения задачи на минимум линию уровня перемещают в антиградиентном направлении

5. Определяем оптимальный план 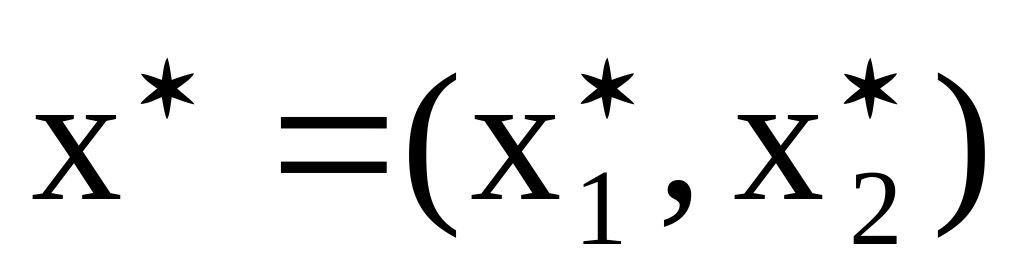и экстре­мальное значение целевой функции .

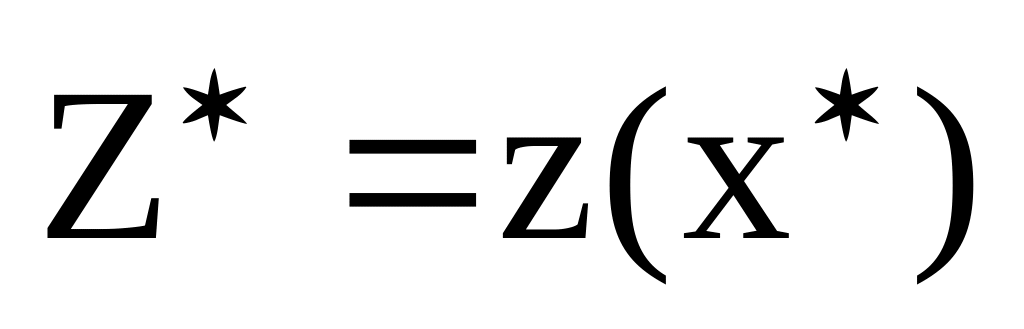Определение оптимального плана выпуска изделий. Рассмотрим на конкретном примере метод графического решения задачи линейного программирования. Фирма выпускает 2 вида мороженого: сливочное и шоколадное. Для изготовления мороженого используются два исходных продукта: молоко и наполнители, расходы которых на 1 кг мороженого и суточные запасы исходных продуктов даны в таблице.

Исходный продукт	Расход исходных продуктов на 1 кг мороженого			Запас, кг
	Сливочное		Шоколадное
Молоко	0,8	0,5		400
Наполнители	0,4	0,8		365

Изучение рынка сбыта показало, что суточный спрос на сливочное мороженое превышает спрос на шоколадное не более чем на 100 кг. Кроме того, установлено, что спрос на шоколадное мороженое не превышает 350 кг в сутки. Отпускная цена 1 кг сливочного мороженого 16 ден. ед., шоколадного — 14 ден. ед. Определить количество мороженого каждого вида, которое должна производить фирма, чтобы доход от реализации продукции был максимальным.

Решение.

Обозначим: xt — суточный объем выпуска сливочного мороженого, кг, х2 — суточный объем выпуска шоколадного мороженого, кг. Составим математическую модель задачи.

Целевая функция будет иметь вид

L(x) = 16x1 + 14x2 _→ max

п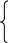 ри ограничениях

0,8х1 +0,5x2 < 400 (ограничение по молоку), (14.5)

0,4х1 +0,8x2 < 365 (ограничение по наполнителям), (14.6)

Х1 -х2 < 100 (рыночное ограничение по спросу), (14.7)

х2 < 350 (рыночное ограничение по спросу), (14.8)

х1≥ 0, х2≥ 0.

Укажем область допустимых (неотрицательных) решений; на

рис. 14.1 показаны ограничивающие линии, соответствующие равен-

ствам в соотношениях (14.5)—(14.8); стрелки указывают области, ко-

торые они ограничивают.

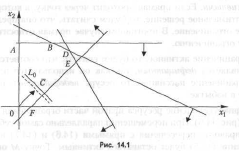
0ABDEF— область допустимых решений. Строим вектор С (16, 14). Линия уровня Lo определяется уравнением (она показана штрихом)

6x1 + 14х2 = const.

Перемещаем линию уровня по направлению вектора С. Точкой выхода 10 из области допустимых решений является точка D, ее координаты определяются как пересечение прямых, заданных ограничениями

Решая эту систему, получим координаты точки D (312,5; 300), которая является оптимальным решением, т. е.

при этом

Итак, максимальный доход от реализации составит 9200 ден. ед. в сутки при выпуске 312,5 кг сливочного и 300 кг шоколадного мороженого.

Экономический анализ задач

Проведем экономический анализ рассмотренной ранее задачи о производстве мороженого.Определим, как влияет на оптимальное решение увеличение или уменьшение запасов исходных продуктов. Для анализа задачи примем, что неравенства системы ограничений могут быть активными или пассивными. Если прямая проходит через точку, в которой находится оптимальное решение, то будем считать, что она представляет

активное ограничение. В противном случае прямая относится к пассивному ограничению.

Если ограничение активное, то будем считать, что соответствующий ресурс является дефицитным, так как он используется полностью. Если ограничение пассивное, то ресурс недефицитный и имеется в фирме в избытке. Рассмотрим увеличение ресурса правой части ограничения (14.5) по молоку (рис. 14.6). При перемещении параллельно самой себе прямой (14.5) вправо до пересечения с прямыми (14.6) и (14.7) в точке М ограничение (14.5) будет оставаться активным. Точку М определим как точку пересечения прямых (14.6) и (14.7):

откуда определяем точку М (370,83; 270,83). Подставляя координаты точки М в неравенство (14.5), получим предельно допустимый суточный запас молока:

при этом величина дохода составит

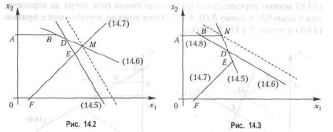
Рассмотрим увеличение ограничения по наполнителям (рис. 14.7).При перемещении параллельно самой себе прямой (14.6) вправо до пересечения с прямыми (14.5) и (14.8) в точке N ограничение (14.6) будет оставаться активным. Точку N определим как точку пересечения прямых:

откуда определяются координаты точки JV (281,25; 350).

Предельно допустимый суточный запас наполнителей можно увеличивать до значения

при этом величина дохода составит

Рассмотрим возможность изменений правой части пассивных ограничений (14.7) и (14.8). Не изменяя оптимальное решение (рис. 14.8), прямую (14.7) можно перемещать параллельно самой себе вверх до пересечения с точкой D (312,5; 300), т. е. правую часть ограничения (14.7) можно уменьшать до величины 312,5 - 300 = 12,5 кг. Прямую (14.7) можно также перемещать параллельно самой себе вниз до пересечения с осью 0Х, в точке Р (500; 0), т. е. правую часть ограничения (14.8) можно увеличивать до 500 кг.

Таким образом, при неизменном оптимальном решении разница в покупательском спросе между сливочным и шоколадным мороженым может изменяться в диапазоне от 12,5 до 500 кг. Аналогично, не изменяя оптимальное решение (рис. 14.5), прямую (14.8) можно перемещать параллельно самой себе вверх до пересечения с осью 0Х2 в точке R (0; 56,25) или вниз до пересечения с прямой(14.6) в точке D (312,5; 300).

2. Алгоритм линейной структуры - это алгоритм, в котором блоки выполняются в указанном порядке, последовательно друг за другом. Программа линейной структуры реализует соответствующий линейный алгоритм.

Чаще всего линейные алгоритмы используются для программирования вычислений по формулам. В этом случае удобно использовать набор встроенных функций Pascal: sin(x) - синус x; cos(x) - косинус x; tan(x)- тангенс x; ln(x) - натуральный логарифм x; exp(x) -показательная функция ex; sqr(x) - квадрат x; sqrt(x) - корень квадратный от х; abs(x) - модуль x.

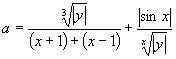
для x = 1,241 y = -0,879

program formula_2; var x, y, a: real; begin x : = 1.241; y : = -0.879; b : = exp(1/3 * ln(abs(y)))/ ((x + 1) + (x - 1)) + abs(sin(x))/ exp(1/x * ln(abs(y))); writeln('Результат: a =', a:12:3); end.