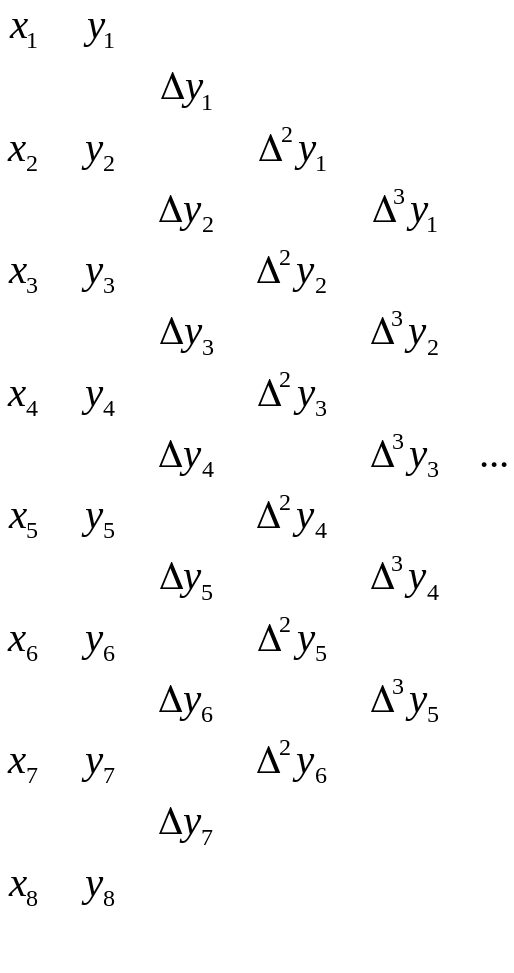Решение систем нелинейных уравнений (Тема №16)

Требуется решить систему нелинейных уравнений следующего вида.

В общем виде прямых решений данная система не имеет, только итерационные.

Метод Зейделя – аналогичен методу Зейделя для систем линейных уравнений.

Численное дифференцирование (Тема №17)

Численное дифференцирование используют в случае таблично-заданной функции или аналитической функции, приведённой к табличному виду, когда её дифференцирование затруднено. Такая функция называется сеточной, получается она как бы набрасыванием дискретной сетки аргументов на .

Дифференцирование таких функций сводится к локальной или глобальной интерполяции или аппроксимации сеточной функции и дифференцированию полученной функции. Как правило принимается равномерная сетка.

Сеточные функции связаны с понятием конечных разностей – шагов сеточной функции и её аргументов. Например для таблица правых конечных разностей выглядит так: - правые разности, - левые разности, - центральные разности. На основе конечных разностей первого порядка строятся разности старших порядков:

При локальной линейной интерполяции дифференцирование производится наиболее просто , где - левые или правые разности, - ошибка аппроксимации первого порядка. При использовании центральных разностей аппроксимация второго порядка, т.е. ошибка меньше. Формулы для старших производных находятся аналогично.

Дифференцирование локальных интерполяционных многочленов Лагранжа для равномерной сетки даёт следующие формулы по центральным разностям:

	’	”
При трёх узлах интерпо-ляции
При пяти уздах интерпо-ляции

*Примечание: последний член выражения – ошибка (погрешность) аппроксимации.

Производные при крайних значениях аргументов сеточной функции находятся по левым и правым разностям и имеют большую ошибку.

При трёх узлах
При пяти узлах
При трёх узлах
При пяти узлах

Для произвольного числа учитываемых узлов произвольной сетки и производной k-порядка зависимость можно найти по методу неопределённых коэффициентов. Пусть при n-узлах интерполяции, где i - узел для которого ищется производная. Коэффициенты можно получить, решив систему линейных уравнений, которая получена из исходного уравнения для n-многочленов вида . Например:

1.
2.
3.

После решения системы линейных уравнений получим следующие результаты: .

Полученное значение будет приближённым. Возможно увеличение порядка точности рассчитанных производных по методу Рунге-Ромберга. Это особенно эффективно при использовании линейных интерполяций. Пусть по сеточной функции определили её производную с шагом и с шагом . Данные производные точности . Тогда – порядок точности увеличивается на единицу.

Например:

составим таблицу соответствия:

	0,8	0,9	1,0
	0,512	0,729	1,0

Требуется определить:

.

Частные производные функции находятся аналогично. При этом сеточная функция не одномерна, а двухмерна и записывается в виде прямоугольной матицы. Есть возможность использовать не только разности по и отдельно , но и смешанно:

Примечание: - индекс по ; - шаг по .