План проведения

Лабораторных работ по курсу ММУ

Лабораторная работа №1 (2 пары)

1. Ознакомление с Excel.

Демонстрация и обучение студентов решению тестовой задачи, приведенной в Методическом пособии №1 по Лабораторным работам, на Excel с помощью надстройки Поиск решения.

2. Самостоятельное решение студентами на Excel с помощью надстройки Поиск решения задач линейного программирования из Методического пособия по выполнению Лабораторной работы №1.

Лабораторная работа №2 (2 пары)

1. Семинарское занятие по методу графического решения задач Линейного программирования. – 1-я п.

2. Семинарское занятие по симплекс-методу решения задач Линейного программирования. – 2-я п.

Лабораторная работа №3 (2 пары)

1. Контрольная работа №1. – 1-я п.

2. Демонстрация и обучение студентов решению тестовой транспортной задачи, приведенной в Методическом пособии №2 по Лабораторным работам, на Excel с помощью надстройки Поиск решения. – 2-я п.

3. Самостоятельное решение студентами на Excel с помощью надстройки Поиск решения транспортных задач из Методического пособия по выполнению Лабораторной работы №2. – 2-я п.

Лабораторная работа №4 (2 пары)

1. Самостоятельное решение студентами на Excel с помощью надстройки Поиск решения транспортных задач из Методического пособия по выполнению Лабораторной работы №2. – 1-я п.

2. Коллоквиум – собеседование преподавателя и студента по теоретической части курса ММУ и решению задач линейного программирования с помощью Excel– 2-я п.

Лабораторная работа №5 (2 пары)

1. Демонстрация и обучение студентов решению тестовых задач с бинарными переменными, приведенных в Методическом пособии №4 по Лабораторным работам, на Excel с помощью надстройки Поиск решения.

2. Самостоятельное решение на Excel задачи с бинарными переменными с помощью надстройки Поиск решения. Варианты – из Методического пособия по выполнению Лабораторной работы №4

План проведения

Лабораторных работ по курсу ММУ

Весенний семестр

Лабораторная работа №1 (2 пары)

Тема «Балансовые экономико-математические модели и их моделирование на Excel»

Тема 1: Экономико-математическая модель межотраслевого баланса (модель Леонтьева).

Тема 2: Экономико-математическая модель международной торговли.

1. Демонстрация и обучение студентов решению тестовых задач, приведенных в Методическом пособии по выполнению Лабораторной работы №5 (см. сайт кафедры meu.rsuh.ru), на Excel с помощью надстройки Поиск решения.

2. Самостоятельное решение студентами на Excel с помощью надстройки Поиск решения задач из Методического пособия по выполнению Лабораторной работы №5.

Лабораторная работа №2 (2 пары)

Тема: Задачи нелинейного программирования.

1. Демонстрация и обучение студентов решению тестовой задачи, приведенной в Методическом пособии по выполнению Лабораторной работы №6 (см. сайт кафедры meu.rsuh.ru), на Excel с помощью надстройки Поиск решения.

2. Самостоятельное решение студентами на Excel с помощью надстройки Поиск решения задач из Методического пособия по выполнению Лабораторной работы №6.

Лабораторная работа №3 (2 пары)

Тема: Сложные проценты и балансовое равенство

1. Демонстрация и обучение студентов решению задач, приведенных в Методическом пособии по выполнению Лабораторной работы №7 (см. сайт кафедры meu.rsuh.ru), на Excel с помощью надстройки Поиск решения.

2. Самостоятельное решение студентами на Excel с помощью надстройки Поиск решения задач из Методического пособия по выполнению Лабораторной работы №7.

Лабораторная работа №4 (2 пары) – семинар и коллоквиум

1-я пара:

Коллоквиум по прочитанному курсу (см. сайт кафедры meu.rsuh.ru).

2-я пара: Семинар по решению задач перед контрольной работой.

Темы:

- нелинейные модели задач нелинейного программирования;

- сложные проценты и балансовое уравнение погашения кредита;

- теория принятия решений. Критерии Лапласа, Вальда, максимаксный, Сэвиджа,

максимального ожидаемого выигрыша и минимального ожидаемого риска

Лабораторная работа №5 (2 пары) – Контрольная работа, коллоквиум

Лабораторная работа № 1

Тема: Задачи линейного программирования и их решение средствами Excel.

Программное обеспечение: Microsoft Excel

Основные сведения

В большинстве оптимизационных задач зависимости между переменными линейны. Линейность предполагает наличие двух свойств пропорциональности и аддитивности.

1. Пропорциональность означает, что вклад каждой переменной в целевую функцию и общий объем потребления соответствующих ресурсов прямо пропорционален уровню (величине) этой переменной.

Аддитивность заключается в том, что целевая функция представляет собой сумму вкладов от различных переменных. Аналогично левая часть каждого ограничения должна представлять собой сумму расходов, каждое слагаемое которой пропорционально величине соответствующей переменной. Если, например, фирма, производит два конкурирующих вида продукции, увеличение сбыта одного из которых отрицательно сказывается на объеме реализации другого, то такая модель не обладает свойством аддитивности.

Математическую модель задачи линейного программирования в общем виде можно записать в виде:

min (max) W = c₁ x₁ + c₂ x₂ +... + c_n x_n; (целевая функция)

при ограничениях:

a₁₁ x₁ + a₁₂ x₂ + ... + a_1n x_n £ (=, ³) b₁

a₂₁ x₁ + a₂₂ x₂ + ... + a_2n x_n £ (=, ³) b₂

. . .

a_m1 x₁ + a_m2 x₂ + ... + a_mn x_n £ (=, ³) b_m

x_j ³ 0, j=1, 2, ... n

Рассмотрим конкретную задачу:

Задача. Руководство фирмы предполагает производить продукцию двух моделей А₁ и А₂. Их производство ограниченно наличием сырья, временем эксплуатации оборудования и денежными кредитами. Для каждого изделия модели А₁ требуется 0,3 м³ древесины, 0,2 часа работы станков и затратить 1,6 денежных единиц, а для изделия модели А₂ - 0,4 м³ древесины, 0,5 часа работы станков и 1 ден. ед. Фирма может получить от своих поставщиков до 170 м³ древесины в неделю и использовать оборудование в течение 160 часов. На финансирование проекта предполагается выделять 800 ден. ед. Сколько изделий каждой модели следует фирме выпускать в неделю, если каждое изделие модели А₁ должно приносить 2 ден. ед. прибыли, а каждое изделие модели А₂ - 4 ден. ед. прибыли?

Построение математической модели

Переменные. Так как нужно определить объемы производства каждого вида моделей продукции, переменными в модели являются:

х₁ - количество выпущенных за неделю изделий модели А₁,

х₂ - количество выпущенных за неделю изделий модели А₂.

Целевая функция. Так как прибыль от реализации 1-го изделия модели А₁ равна 2 денежным единицам, недельный доход от ее продажи составит 2*х₁ ден. ед. Аналогично доход от реализации х₂ штук изделия модели А₂ составит 4*х₂ ден. ед. в неделю.

При допущении независимости объемов сбыта каждой из моделей общий доход равен сумме двух слагаемых - дохода от продажи модели А₁ и дохода от продажи модели А₂.

Обозначив общий доход через W, можно дать следующую математическую формулировку целевой функции: определить (допустимые) значения х₁ и х₂, максимизирующие величину общего дохода W = 2*х₁ + 4*х₂.

Ограничения. При решении рассматриваемой задачи должны быть учтены ограничения на расход древесины, время эксплуатации оборудования и финансовые возможности фирмы.

Ограничение на расход древесины можно записать следующим образом:

0,3 х₁ + 0,4 х₂ £ 170,

здесь 0,3 х₁ расход древесины на выпуск недельного объема в х₁ изделий модели А₁, а 0,4 х₂ - х₂ изделий модели А₂. Суммарный расход древесины на выпуск двух моделей не может превышать максимально возможный запас древесины в 170 м³.

Ограничение на время использование оборудования можно записать следующим образом:

0,2 х₁ + 0,5 х₂ £ 160,

здесь: 0,2 х₁ - количество часов работы оборудования в неделю для выпуска х₁ изделий модели А, а 0,5 х₂ - х₂ изделий модели В в неделю. Время эксплуатации станков для выпуска обоих моделей не может превышать максимально возможный запас времени работы оборудования в160 часов.

Ограничение на использование финансов можно записать следующим образом:

1,6 х₁ + 1,0 х₂ £ 800,

здесь: 1,6*х₁ - количество денежных ресурсов расходуемых в неделю для выпуска х₁ изделий модели А, а 1,0*х₂ - х₂ изделий модели В в неделю. Сумма затрат на выпуск обоих моделей не может превышать максимально возможный запас финансов.

Поскольку х₁ и х₂ выражают еженедельный объём выпускаемых изделий, то они не могут быть отрицательными, т.е. х₁ ³ 0 и х₂ ³ 0 (условие не отрицательности переменных).

Итак, математическую модель задачи № 1 можно записать следующим образом:

max W= 2 х₁ +4 х₂ (целевая функция) (1)

при ограничениях:

0,3 х₁ + 0,4 х₂ £ 170 (2)

0,2 х₁ + 0,5 х₂ £ 160 (3)

1,6 х₁ + х₂ £ 800 (4)

х₁ ³ 0, х₂ ³ 0 (5)

Процесс решения задачи средствами Microsoft Excel

Рис. 1. Фрагмент Листа рабочей книги с исходными данными

Вызовите Microsoft Excel. В новой рабочей книге переименуйте "Лист№1" в ЛР 1 Вариант №… Отчет (Фамилия № группы)

 

Задание Исходных данных задачи

Начиная с ячейки с именем А1 на Листе окна Excel постройте следующую таблицу (рис. 1.):

В ячейки с адресами В2:С4 – двоеточие означает диапазон ячеек, начинающийся с ячейки с адресом В2 и заканчивающийся ячейкой с адресом С4 – заносятся коэффициенты при неизвестных х₁ и х₂ в ограничениях (2)–(4).

После занесения в ячейку числа или формулы необходимо нажать клавишу ENTER.

В ячейки с адресами В5:С5 занесены коэффициенты в целевой функции (1).

В строке Переменные ячейки В6:С6 пусты; в них после решения задачи, будут занесены рассчитанные значения переменных х₁ и х₂ .

Рис. 2. Фрагмент Листа Excel на экране с диалоговым окном Поиск решения

В столбце Ограничения в ячейки G2:G4 занесены формулы для расчеты левых частей ограничений (2)–(5). Каждая формула начинается со знака «=». Для введения формулы в ячейку G2, щелкните мышью на ячейке с этим адресом (ячейка будет обведена жирной рамкой). В ячейке напечатайте следующее: =СУММПРОИЗВ(B2:C2;B6:C6). Здесь записано, что числа в ячейках с адресами В2:С2 умножаются на соответствующие им числа в ячейках В6:С6 и затем результаты произведений просуммированы. Тем самым задано ограничение (2). Задание ограничений (3) и (4) содержится в ячейках G3, G4; в них напечатаны напечатайте формулы =СУММПРОИЗВ(B3:C3;B6:C6) и =СУММПРОИЗВ(B4:C4;B6:C6) соответственно.

В ячейку В7 занести формулу =СУММПРОИЗВ(B5:C5;B6:C6), которой записана целевая функция (1). В эту же ячейку бедет занесено вычисленное значение целевой функции.

 

Решение задачи

Поставить курсор мыши в ячейку В7 и нажать на левую кнопку мыши – туда после решения задачи, будет занесено вычисленное значение целевой функции.

Войти в меню Сервис, выбрать в нем Поиск решения и щелкнуть на нем левой кнопкой мыши. На экране появится диалоговое окно Поиск решения (рис. 2). В поле Установить целевую ячейку занести $B$7. Для этого проще всего установить курсор мыши внутрь ячейки, щелкнуть в ней левой кнопкой мыши, затем щелкнуть мышью на ячейке В7.

Поскольку ищется максимум целевой функции, то после слова Равной выделим Максимальному значению, щелкнув в кружочке мышью.

Рис. 3. Диалоговое окно Добавление ограничения

В поле Изменяя ячейки занесем диапазон $B$6:$C$6 так как именно эти ячейки отведены под значения вычисляемых переменных. Для этого поставим курсор в поле Изменяя ячейки , затем поставим курсор на ячейке В6 и при нажатой левой кнопке мыши переведем курсор на ячейку С6. В поле Изменяя ячейки появится необходимый диапазон ячеек.

В поле Ограничения занесем ограничения (2)–(5). Для этого щелкнем мышью на кнопке Добавить. Появится диалоговое окно Добавление ограничения (рис. 3).

В поле Ссылка на ячейку поставить курсор мыши в поле, затем поставить курсор на ячейку G2, где задана формула ограничения. В среднее поле, щелкнув на кнопке со стрелочкой, занесем соответствующий знак неравенства. В поле Ограничение занесем правую часть ограничения, расположенную в ячейке Е2. Щелкнуть на кнопке ОК. Попадаем снова в поле Поиск решения. Затем повторяя описанные выше действия, заносим остальные ограничения (рис. 2).

Рис. 4. Диалоговое окно Параметры поиска решения

Снова в поле Поиск решения (рис. 2). Щелкнуть мышью на кнопке Параметры.

Рис. 5. Диалоговое окно Результаты поиска решения

На экране появится диалоговое окно Параметры поиска решения. В этом окне (рис. 4) устанавливаются параметры поиска решения. Здесь отметить квадратики Линейная модель, Неотрицательные значения, Автоматическое масштабирование. Щелкнем на кнопке ОК.

Снова попадаем в диалоговое окно Поиск решения. В этом окне (рис. 2) щелкнем левой кнопкой мыши на кнопку Выполнить. На экран

выводится окно Результаты поиска решения (рис. 5).

Одновременно на Листе экрана также появляются результаты решения задачи (рис. 6): В столбце Ограничения выводятся их рассчитанные значения . В строке переменные – значения рассчитанных переменных х₁ и х₂ . В ячейке с целевой функцией – рассчитанное значение целевой функции.

Рис. 6. Результаты решения задачи расположенные на Листе экрана

Итак найдено решение: х₁ = 300, х₂ = 200, Fmax = 1400.

В окне Результаты поиска решения содержится тип отчета: Результаты, Устойчивость, Пределы. Для получения всех видов отчетов надо щелкнуть кнопкой мыши на каждом из них – соответствующие строчки будут закрашены – а затем на ОК. Отчеты отображаются в нижней строке Листа на экране Excel. Для их вызова необходимо щелкнуть на соответствующем отчете.

В отчете по результатам (рис. 7) приведены значения неизвестных и целевой функции, а также данные о выполнении ограничений. В графе Статус указаны связанные и несвязанные переменные.

В отчете по устойчивости (рис. 8) приведены границы устойчивости неизвестных задачи – допустимое увеличение и уменьшение коэффициентов целевой функции, границы устойчивости двойственных оценок. В графе Нормированная стоимость элемент этой графы показывает, на сколько уменшится значение функции, если в решении переменную увеличить на единицу.

В отчете по пределам (рис. 9) показаны нижние и верхние пределы изменения неизвестных и значения целевой функции при этих изменениях.

 

 

Рис. 7. Отчет по результатам

 

Рис. 8 Отчет по устойчивости

 

Рис. 9. Отчет по пределам

Индивидуальные задания

Задание 1. Небольшая фабрика изготовляет два вида красок: для наружных (№1) и внутренних (№2) работ. Продукция обоих видов поступает в оптовую продажу. Для производства красок используются два исходных продукта – А и В. Максимально возможные суточные запасы этих продуктов составляют 6 и 8 т соответственно. Расходы А и В на 1т соответствующих красок приведены в табл.

Изучение рынка сбыта показало, что суточный спрос на краску для внутренних работ (№2) никогда не превышает спрос на краску для наружных работ (№1) более чем на 1 т. Кроме того, установлено, что спрос на краску № 2 никогда не превышает 2 т в сутки.

Прибыль от реализации одной тонны красок № 1 равна 3 тыс. денежных единиц, а для краски № 2 – 2 тыс. ден. ед.

 

Исходный продукт	Расход исходных продуктов (в тоннах) на тонну краски		Максимально возможный запас, т
	Краска № 1	Краска № 2
А	1	2	6
В	2	1	8

 

Какое количество краски каждого вида должна производить фабрика, чтобы доход от реализации продукции был максимальным?

 

Задание 2. Пошивочное предприятие намечает выпуск двух видов костюмов – мужских и женских. На женский костюм требуется 1 м шерсти, 2м лавсана и 1чел/день трудозатрат. На мужской костюм требуется 3,5 м шерсти, 0,5 м лавсана и 1чел/день трудозатрат. Всего имеется 350 м шерсти, 240 м лавсана и 150 чел/день трудозатрат. Определить сколько костюмов каждого вида необходимо сшить, чтобы обеспечить максимальную прибыль, если прибыль от реализации женского костюма составляет 10 денежных единиц, от мужского – 20 денежных единиц. При этом следует иметь в виду, что необходимо сшить не менее 60 мужских костюмов.

 

Задание 3. Для производства двух видов изделий А и В предприятие использует три вида сырья. Нормы расхода сырья каждого вида на изготовление единицы продукции данного вида приведены в табл. В ней же указаны прибыль от реализации одного изделия каждого вида и общее количество сырья данного вида, которое может быть использовано предприятием.

Учитывая, что изделия А и В могут производиться в любых соотношениях (сбыт обеспечен), требуется составить такой план их выпуска, при котором прибыль предприятия от реализации всех изделий является максимальной.

 

Вид сырья	Нормы расхода сырья (кг) на одно изделие		Общее количество сырья (кг)
	А	В
1	12	4	300
2	4	4	120
3	3	12	252
Прибыль от реализации одного изделия (руб)	30	40

 

Задание 4. Для производства столов и шкафов мебельная фабрика использует необходимые ресурсы. Нормы затрат ресурсов на одно изделие данного вида, прибыль от реализации одного изделия и общее количество имеющихся ресурсов каждого вида приведены в табл.

 

Ресурсы	Нормы затрат ресурсов на одно изделие		Общее количество ресурсов
	стол	шкаф
Древесина (м3):
1 вида	0,2	0,1	40
2 вида	0,1	0,3	60
Трудоемкость (человеко-час)	1,2	1,5	371,4
Прибыль от реализации одного изделия (руб)	6	8

 

Определить, сколько столов и шкафов следует изготовлять, чтобы прибыль от их реализации была максимальной.

 

Задание 5. Для производства двух видом изделий А и В используется токарное, фрезерное и шлифовальное оборудование. Нормы затрат времени для каждого из типов оборудования на одно изделие данного вида приведены в табл. В ней же указан общий фонд рабочего времени каждого из типов оборудования, а также прибыль от реализации одного изделия.

Найти план выпуска изделий А и В, обеспечивающий максимальную прибыль от их реализации.

 

Тип оборудования	Затраты времени (оборуд.-час) на обработку одного изделия		Общий фонд полезного рабочего времени оборудования (ч)
	А	В
Фрезерное	10	8	168
Токарное	5	10	180
Шлифовальное	6	12	144
Прибыль от реализации одного изделия (руб)	14	18

 

Задание 6. На мебельной фабрике из стандартных листов фанеры необходимо вырезать заготовки трех видов в количествах, соответственно равных 24, 31 и 18 шт. Каждый лист фанеры может быть разрезан на заготовки двумя способами. Количество получаемых заготовок при данном способе раскроя приведено в табл. В ней же указана величина отходов, которые получаются при данном способе раскроя одного листа фанеры.

 

Вид заготовки	Количество заготовок (шт) при раскрое по способу
	1	2
1	2	6
2	5	4
3	2	3
Величина отходов (см2)	12	16

 

Определить, сколько листов фанеры и по какому способу следует раскроить так, чтобы было получено не меньше нужного количества заготовок при минимальных отходах.

 

Задание 7. На звероферме могут выращиваться черно-бурые лисицы и песцы. Для обеспечения нормальных условий их выращивания используется три вида кормов. Количество корма каждого вида, которое должны ежедневно получать лисицы и песцы, приведено в табл. В ней же указаны общее количество каждого вида, которое может быть использовано зверофермой, и прибыль от реализации одной шкурки лисицы и песца.

 

Вид корма	Количество единиц корма, которое ежедневно должны получать		Общее количество корма
	Лисица	Песец
1	2	3	180
2	4	1	240
3	6	7	426
Прибыль от реализации одной шкурки (руб)	16	12

 

Определить, сколько лисиц и песцов следует выращивать на звероферме, чтобы прибыль от реализации их шкурок была максимальной.

 

Задача 8. Компания производит полки для ванных комнат двух размеров – А и В. Агенты по продаже считают, что в неделю на рынке может быть реализовано до 550 полок. Для каждой полки типа А требуется 2 м2 материала, а для полки типа В – 3 м2 материала. Компания может получить до 1200 м2 материала в неделю. Для изготовления одной полки типа А требуется 12 мин машинного времени, а для изготовления одной полки типа В – 30 мин; машину можно использовать 160 час в неделю. Если прибыль от продажи полок типа А составляет 3 денежных единицы, а от полок типа В – 4 ден. ед., то сколько полок каждого типа следует выпускать в неделю?

 

Задача 9. Небольшая фирма производит два вида продукции: столы и стулья. Для изготовления одного стула требуется 3 фута древесины, а для изготовления одного стола – 7 футов. На изготовление одного стула уходит 2 часа рабочего времени, а на изготовление стола – 8 часов. Каждый стул приносит 1 долл. прибыли, а каждый стол – 3 долл. Сколько стульев и сколько столов должна изготовить эта фирма, если она располагает 420 футами древесины и 400 часами рабочего времени и хочет получить максимальную прибыль?

 

Задача 10. Некоторая фирма выпускает два набора удобрений для газонов: обычный и улучшенный. В обычный набор входит 3 фунта азот- ных, 4 фунта фосфорных и 1 фунт калийных удобрений, а в улучшенный – 2 фунта азотных, 6 фунтов фосфорных и 3 фунта калийных удобрений. Известно, что для некоторого газона требуется по меньшей мере 10 фунтов азотных, 20 фунтов фосфорных и 7 фунтов калийных удобрений. Обычный набор стоит 3 долл., а улучшенный – 4 долл. Какие и сколько наборов удобрений нужно купить, чтобы обеспечить эффективное питание почвы и минимизировать стоимость?

Задача 11. На имеющихся у фермера 400 акрах земли он планирует посеять кукурузу и сою. Сев и уборка кукурузы требует на каждый акр 200 долл. затрат, а сои – 100 долл. На покрытие расходов, связанных с севом и уборкой, фермер получил ссуду в 60 тыс. долл. Каждый акр, засеянный кукурузой, приносит 40 бушелей, а каждый акр, засеянный соей, – 80 бушелей. Фермер заключил договор на продажу, по которому каждый бушель кукурузы принесет ему 3 долл., а каждый бушель сои – 1 долл. Однако, согласно этому договору, фермер обязан хранить убранное зерно в течение нескольких месяцев на складе, максимальная вместимость которого равна 21 тыс. бушелей. Фермеру хотелось бы знать, сколько акров нужно засеять каждой из этих культур, с тем чтобы получить максимальную прибыль.

 

Задача 12. На заводе используется сталь трех марок: А, В, С, запасы которых равны соответственно 10, 16 и 12 ед. Завод выпускает два вида изделий. Для изделия 1 требуется по одной единице стали всех марок. Для изделия 2 требуется 2 единицы стали марки В, одна – марки С и не требуется сталь марки А. От реализации единицы изделия вида 1 завод получает 300 руб. прибыли, а вида 2 – 200 руб. Составить план выпуска продукции, дающий наибольшую прибыль

 

Задача 13. Производитель безалкогольных напитков располагает двумя разливочными машинами А и В по 4 шт. каждой. Машина А спроектирована для пол-литровых бутылок, а машина В – для литровых. Машина А может выпускать до 50 пол-литровых бутылок в 1 мин, а машина В – до 30 литровых бутылок в 1 мин. Каждая из машин работает ежедневно по 6 час, при пятидневной рабочей неделе. Прибыль от продажи одной пол-литровой бутылки составляет 4 цента, а одной литровой бутылки – 10 центов. Недельная продукция не может превосходить 259200 л; рынок за неделю принимает не более 288000 пол-литровых бутылок и не более 180000 литровых бутылок. Сколько бутылок пол-литровых и литровых должна выпускать каждая машина А и В за 1 мин., чтобы максимизировать недельную прибыль производителя от продажи безалкогольных напитков, при имеющихся средствах.

 

Литература

1. Таха Х. Введение в исследование операций, в 2-х книгах. Пер. с англ.. – М.: Мир, 1985

2. Акулич И.Л. Математическое программирование в примерах и задачах. – М.: Высш. Шк., 1986

3. Шикин Е.В., Чхартишвили А.Г. Математические методы и модели в управлении. – М., Дело, 2002

4. Банди Б. Основы линейного программирования. Пер. с англ. – М.: Радио и связь, 1989

Порядок выполнения работы

На лабораторную работу каждый студент приносит чистую, неиспользованную дискету МД 3,5'. На этой дискете будут содержаться файлы с исходными данными и результатами по всем выполненным работам.

Задание. Получить вариант задачи у преподавателя. Составить математическую модель задачи. Найти оптимальное решение задачи в Excel и показать результаты поиска решения преподавателю на экране компьютера. Отчет составляет на МД.

Отчет. Отчет по лабораторной работе представляется на дискете студента и должен содержать файл с названием ЛР 2 Вариант №… Отчет (Фамилия № группы).

Состав отчета, записанный на МД:

- математическая модель задачи, предъявляемая преподавателю (может быть написана от руки).

- Рабочий лист Excel с исходными данными и математической моделью, протокол решения задачи, куда входят:

- результаты решения в виде отчета Результаты

Отчет на компьютере и МД демонстрируется преподавателю на данном лабораторном занятии.

Сдача лабораторной работы преподавателю принимается только при наличии у студента МД с результатами расчета и отметки у преподавателя о выполненной лабораторной работе. Во время сдачи лабораторной работы студент должен уметь проводить анализ полученных результатов.

 

Лабораторная работа № 2.

Тема: Транспортные задачи и их решение средствами Excel.

Программное обеспечение: Microsoft Excel

Основные сведения

Общая постановка транспортной задачи состоит в определении оптимального плана перевозок некоторого однородного груза из m пунктов отправления А₁, А₂, …, А_m в n пунктов назначения В₁, В₂, …, В_n . При этом в качеств критерия оптимальности обычно берется либо минимальная стоимость перевозок всего груза, либо минимальное время его доставки. Рассмотрим транспортную задачу, в качестве критерия оптимальности которой взята минимальная стоимость перевозок всего груза. Обозначим c_ij тарифы перевозки единицы груза из i-го пункта отправления в j-й пункт назначения, через a_i – запасы груза в i-ом пункте отправления, через b_j – потребности в грузе в j-ом пункте назначения, а через x_ij – количество единиц груза, перевозимого из i-го пункта отправления в j-й пункт назначения. Тогда математическая постановка зачади состоит в определении минимального значения функции

(1)

при условиях

(2)

(3)

(4)

Поскольку переменные удовлетворяют системам линейных уравнений (2) и (3) и условию неотрицательности (4), обеспечиваются доставка необходимого количества груза в каждый из пунктов назначения, вывоз имеющегося груза из всех пунктов отправления, а также исключаются обратные перевозки.

Очевидно, общее наличие груза у поставщиков равно , а общая потребность в грузе в пунктах назначения равна 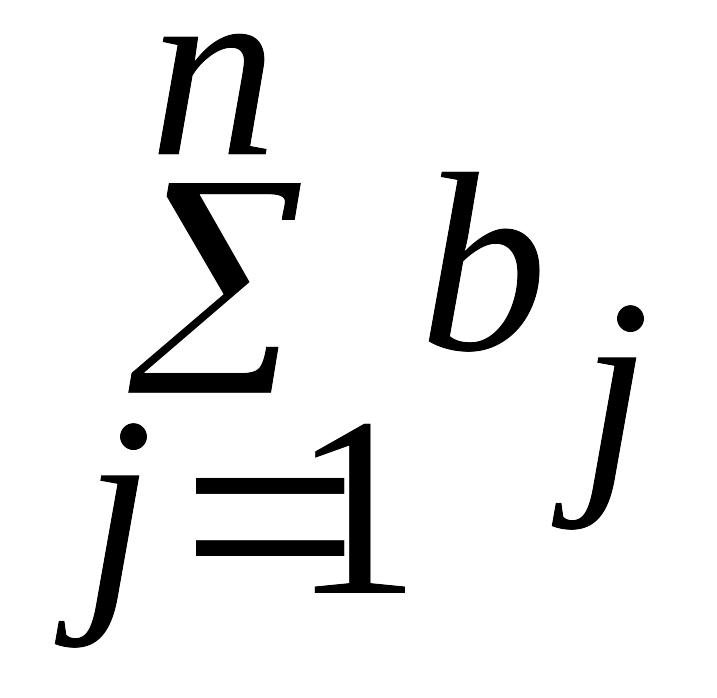единиц. Если общая потребность в грузе в пунктах назначения равна запасу груза в пунктах отправления, т.е.

= , (5)

то модель такой транспортной задачи называется закрытой. В противном случае – открытой.

В случае превышения запаса над потребностью, т.е.

>

вводится фиктивный (n+1) потребитель (или пункт назначения) с потребностью равной b_n+1 = – , а соответствующие транспортные тарифы от всех поставщиков до фиктивного потребителя полагаются равными нулю. Полученная задача становится закрытой транспортной задачей, для которой выполняется равенство (5).

В случае превышения потребности некоторого потребителя над общими запасами, т.е.

<

вводится фиктивный (m+1) пункт отправления с запасом груза в нем, равным с потребностью равной a_m+1 = – , а соответствующие транспортные тарифы от фиктивного поставщика до всех потребителей полагаются равными нулю. Полученная задача становится закрытой транспортной задачей, для которой выполняется равенство (5).

 

Рассмотрим конкретную задачу:

 

Задача. Четыре предприятия данного экономического района для производства продукции получают сырье от трех поставщиков. Потребности в сырье каждого из предприятий соответственно равны 900, 600, 800 и 600 ед. Сырье сосредоточено в трех местах его получения, а запасы соответственно равны 600, 800 и 1000 ед. На каждое из предприятий сырье может завозиться из любого пункта его получения. Тарифы перевозок являются известными величинами и задаются матрицей

.

Составить такой план перевозок, при котором общая стоимость перевозок является минимальной.

Построение математической модели

Обозначим через x_ij количество единиц сырья, перевозимого из i-го пункта его получения на j-е предприятие. Задача является открытой, так как сумма запасов грузов 600 + 800 + 1000 = 2400 в местах отправления, не равна сумме потребностей грузов в местах назначения 900 + 600 + 800 + 600 = 2900. Так как потребности в грузах превышают их запасы, то вводим фиктивного поставщика с номером 4, у которого запас груза равен 2900 – 2400 = 500. В этом случае общий запас станет равным 2900 и мы получим закрытую транспортную задачу. При этом все тарифы от фиктивного поставщика ко всем потребителям груза полагаются равными нулю. В матрице тарифов появится четвертая строка, в которой стоят все нули. Целевая функция не изменится.

Условия доставки и вывоза необходимого и имеющегося сырья обеспечиваются за счет выполнения следующих равенств:

x₁₁ + x₁₂ + x₁₃.+ x₁₄.= 600 (6)

x₂₁ + x₂₂ + x₂₃.+ x₂₄.= 800 (7)

x₃₁ + x₃₂ + x₃₃.+ x₃₄.= 1000 (8)

x₄₁ + x₄₂ + x₄₃.+ x₄₄.= 500 (9)

x₁₁ + x₂₁ + x₃₁. + x₄₁ = 900 (10)

x₁₂ + x₂₂ + x₃₂..+ x₄₂ = 600 (11)

x₁₃ + x₂₃ + x₃₃. + x₄₃ = 800 (12)

x₁₄ + x₂₄ + x₃₄. + x₄₄= 600 (13)

При данном плане перевозок , общая стоимость перевозок составит

F = 4x₁₁ + 3x₁₂ + 2₁₃.+ 1x₁₄ + 2x₂₁ + 1x₂₂.+ 7x₂₃ +

+ 9x₂₄ + 3x₃₁ + 6x₃₂.+ + 8x₃₃ + 4x₃₄ → min. (14)

Таким образом, математическая постановка задачи состоит в нахождении такого неотрицательного решения системы линейных уравнений (6)–(13), при котором целевая функция (14) принимает минимальное значение.

 

Решение задачи средствами Microsoft Excel

Рис. 1. Фрагмент Листа рабочей книги с исходными данными

Вызовите Microsoft Excel. В новой рабочей книге переименуйте "Лист№1" в ЛР 2 Вариант №… Отчет (Фамилия № группы)

 

Задание Исходных данных задачи

Начиная с ячейки с именем А1 на Листе окна Excel постройте следующую таблицу (рис. 1.):

Ячейки с адресами В4:Е7 резервируются для переменных (рис. 1) – это изменяемые ячейки. В ячейках F4:F7 заносятся запасы грузов в пунктах отправления, включая и

фиктивный, в ячейках B9:E9 заносятся потребности (спрос) в грузах в пунктах назначения.

После занесения в ячейку числа или формулы необходимо нажать клавишу ENTER.

В ячейки с адресами В15:Е18 занесены коэффициенты матрицы затрат на перевозку грузов.

Ячейки G4:G7 содержат формулы для расчета ограничений (6) – (9). Формула ограничения (6) занесена в ячейку G4 и имеет вид =СУММ(B4:E4). Соответственно ограничения (7), (8) и (9) занесены в ячейки G5, G6 и G7 в виде формул =СУММ(B5:E5), =СУММ(B6:E6) и =СУММ(B7:E7).

В ячейках В10:Е10 содержатся формулы ограничений (9)–(12), которые соответственно имеют вид: =СУММ(B4:B7), =СУММ(C4:C7), =СУММ(D4:D7), =СУММ(E4:E7).

В ячейки В15:Е18 занесены матрица затрат на перевозки между всеми пунктами отправления груза и назначения. Четвертая строка этой матрицы соответствует перевозкам от фиктивного поставщика.

Формула для расчета Целевой функции (13) занесена в ячейку С19 и имеет вид: =СУММПРОИЗВ(B15:E18;B4:E7). В эту же ячейку будет занесено вычисленное значение целевой функции.

Рис. 2. Диалоговое окно Поиск решения с занесенными формулами ограничений

 

Решение задачи

Поставить курсор мыши в ячейку С19, в которой будет содержаться вычисленное значение целевой функции, и нажать на левую кнопку мыши.

Войти в меню Сервис, выбрать в нем Поиск решения и щелкнуть на нем левой кнопкой мыши. На экране появится диалоговое окно Поиск решения (рис. 2).

 

Рис. 3. Диалоговое окно Добавление ограничения

 

Рис. 4. Диалоговое окно Параметры поиска решения

В поле Установить целевую ячейку заносится $С$19. Для этого проще всего установить курсор мыши внутрь ячейки, щелкнуть в ней левой кнопкой мыши, затем щелкнуть мышью на ячейке С17.

Поскольку ищется минимум целевой функции, то после слова Равной выделим Минимальному значению, щелкнув в кружочке мышью.

В поле Изменяя ячейки занесем диапазон $B$4:$Е$7 так как именно эти ячейки отведены под значения вычисляемых переменных. Для этого поставим курсор в поле Изменяя ячейки , затем поставим курсор на ячейке В4 и при нажатой левой кнопке мыши переведем курсор на ячейку Е7. В поле Изменяя ячейки появится необходимый диапазон ячеек.

В поле Ограничения занесем ограничения (6)–(12), (14), а также условия неотрицательности переменных. Для этого щелкнем мышью на кнопке Добавить. Появится диалоговое окно Добавление ограничения (рис. 3). Третье ограничение (рис. 2) занесено следующим образом: в окне Поиск решения щелкнуть на кнопке Добавить. Откроется диалоговое окно Добавление ограничения. В поле Ссылка на ячейку поставить курсор мыши нажать на левую ее кнопку. Затем поставить курсор мыши на ячейку G4, глее введено ограничение и при нажатой кнопке мыши провести вплоть до ячейки с адресом G7. В среднем поле окна Добавить ограничения выбираем знак равенства, а в последнем поле описанным выше способом заносим ячейки F4:F7, содержащие запасы поставщиков. Аналогично заносятся и другие ограничения (рис. 2).

Снова в поле Поиск решения (рис. 2). Щелкнуть мышью на кнопке Параметры.

На экране появится диалоговое окно Параметры поиска решения. В этом окне (рис. 4) устанавливаются параметры поиска решения. Здесь отметить квадратики Линейная модель, Неотрицательные значения, Автоматическое масштабирование. Щелкнем на кнопке ОК.

Рис. 5. Диалоговое окно Результаты поиска решения

Снова попадаем в диалоговое окно Поиск решения. В этом окне (рис. 2) щелкнем левой кнопкой мыши на кнопку Выполнить. На экран выводится окно Результаты поиска решения (рис. 5).

Одновременно на Листе экрана также появляются результаты решения задачи (рис. 6): в столбце и строке Ограничения выводятся их рассчитанные значения . В ячейках В4:Е7 содержатся значения рассчитанных переменных – объемов перевозок от каждого пункта отправления к каждому пункту назначения. В ячейке с целевой функцией С19 – рассчитанное значение целевой функции.

Итак найдено решение: F_min = 5200, x₁₁ = 0, x₁₂ = 0, x₁₃.= 300, x₁₄ = 300, x₂₁ = 200, x₂₂.= 600, x₂₃ = 0, x₂₄ =0, x₃₁ = 700, x₃₂.= 0, x₃₃ = 0, x₃₄.= 300, и фиктивные переменные x₄₁ = x₄₂ =+x₄₄.= 0, x₄₃.= 500.

Рис. 6. Результаты решения транспортной задачи в окне Excel

 

Замечание. Прежде чем приступать к решению транспортной задачи данного варианта, необходимо проверить баланс между общим запасом груза у поставщиков и общей потребностью у потребителей. Если соответствующие суммы не равны между собой, необходимо ввести либо фиктивного поставщика, либо фиктивного потребителя (см. выше).

Индивидуальные задания:

Вариант № 1.

Необходимо решить транспортную задачу: минимизировать расходы на доставку продукции заказчикам со складов фирмы, учитывая следующие затраты на доставку одной единицы продукции, объём заказа и количество продукции, хранящейся на каждом складе. Тарифы на перевозку единицы продукции, объёмы запасов продукции на складах, а также объёмы заказанной продукции представлены в таблице №1.

Склад	Магазины заказчики					Запасы на складе (ед. прод)
	“Анна”	“Вада”	“Ева”	“Алла”	“Мех”
“Таганка”	1	3	4	5	2	20
“ВВЦ”	2	1	1	4	5	15
“Щёлково”	1	3	3	2	1	40
“Коньково”	3	1	4	2	3	15
Объём заказа (ед. прод)	15	10	25	5	9

 

Вариант № 2.

Необходимо решить транспортную задачу: минимизировать расходы на доставку продукции заказчикам со складов фирмы, учитывая следующие затраты на доставку одной единицы продукции, объём заказа и количество продукции, хранящейся на каждом складе :

Таблица тарифов на перевозку продукции и объёмов запасов на складе и заказов :

Магазин   Склад	“Росс- тек”	“Шер”	“Тка-ни”	“Мода”	“Вита”	Запасы на складе (ед.прод)
Иваново	12	14	32	20	3	54
Москва	8	10	12	24	12	32
Новгород	6	8	12	24	8	85
Серпухов	10	18	4	8	9	162
Объём заказа (ед.прод)	100	70	30	45	50

 

Вариант № 3 .

Необходимо решить транспортную задачу: минимизировать расходы на доставку продукции заказчикам со складов фирмы, учитывая следующие затраты на доставку одной единицы продукции, объём заказа и количество продукции, хранящейся на каждом складе :

Таблица тарифов на перевозку продукции и объёмов запасов на складе и заказов :

Магазин   Склад	“Всё для дома”	“Здоровый сон”	“Фея”		“Ночное царство”		“Мех”	Запасы на складе (ед.прод)
“Вороново”	1	3	4	5			2	20
“Фили”	2	1	1	4			5	15
“Беляево”	1	3	3	2			1	40
“Выхино”	3	1	4	2			3	15
Объём заказа (ед.прод)	15	10	25	5			9

 

Вариант № 4 .

Необходимо решить транспортную задачу: минимизировать расходы на доставку продукции заказчикам со складов фирмы, учитывая следующие затраты на доставку одной единицы продукции, объём заказа и количество продукции, хранящейся на каждом складе :

Таблица тарифов на перевозку продукции и объёмов запасов на складе и заказов :

Магазин   Склад	ВДНХ	Юго—Запад-ная	Фили	Арбат-ская	Соколь-ники	Запасы на складе (ед.прод)
Пролетарская	10	8	3	15	16	60
Митино	7	5	9	4	6	30
Строгино	2	0	14	5	20	40
Объём заказа (ед.прод)	10	20	40	30	65

 

Вариант № 5.

Необходимо решить транспортную задачу: минимизировать расходы на доставку продукции заказчикам со складов фирмы, учитывая следующие затраты на доставку одной единицы продукции, объём заказа и количество продукции, хранящейся на каждом складе :

Таблица тарифов на перевозку продукции и объёмов запасов на складе и заказов :

 

Магазин   Склад	Тверь	Рязань	Тула	Чехов	Запасы на складе (ед.прод)
Москва	5	3	7	2	25
Санкт-Петербург	2	6	4	5	36
Саратов	3	7	1	9	40
Самара	6	4	8	3	50
Объём заказа (ед.прод)	20	45	15	25

 

Вариант № 6 .

Необходимо решить транспортную задачу: минимизировать расходы на доставку продукции заказчикам со складов фирмы, учитывая следующие затраты на доставку одной единицы продукции, объём заказа и количество продукции, хранящейся на каждом складе :

Таблица тарифов на перевозку продукции и объёмов запасов на складе и заказов :

Магазин   Склад	Сокол	Риж-ская	ВДНХ	Киев-ская	Царицыно	Запасы на складе (ед.прод)
Пражская	3	7	3	4	0	50
Волжская	6	2	5	7	4	55
Курская	8	5	8	3	4	60
Савёловская	1	3	6	5	3	20
Объём заказа (ед.прод)	30	60	40	20	15

Вариант № 7 .

Необходимо решить транспортную задачу: минимизировать расходы на доставку продукции заказчикам со складов фирмы, учитывая следующие затраты на доставку одной единицы продукции, объём заказа и количество продукции, хранящейся на каждом складе :

Таблица тарифов на перевозку продукции и объёмов запасов на складе и заказов :

Магазин   Склад	Новго-род	Москва	Самара	Саратов	Тверь	Запасы складов (ед.прод)
Нижний Новгород	4	0,5	2	1	3	35
Саратов	5	2	0,5	0	2	25
Самара	4	2	0	0,5	2	30
Санкт- Петербург	2	1	4	4,5	3	40
Объём заказа (ед.прод)	30	15	25	30	25

Вариант № 8 .

Необходимо решить транспортную задачу: минимизировать расходы на доставку продукции заказчикам со складов фирмы, учитывая следующие затраты на доставку одной единицы продукции, объём заказа и количество продукции, хранящейся на каждом складе :

Таблица тарифов на перевозку продукции и объёмов запасов на складе и заказов :

Магазин   Склад	“Колбасы”	“Мясо”	“Мясные деликатесы”	“Ди-на”	Запасы на складе (ед.прод)
Черкизово	1	0	0,5	2	45
Царицыно	3	2	4	1	50
Бородино	0	2,5	2	3	15
Вешняки	4	3	1,5	2	20
Объём заказа (ед.прод)	30	40	20	25

 

Вариант № 9.

Необходимо решить транспортную задачу: минимизировать расходы на доставку продукции заказчикам со складов фирмы, учитывая следующие затраты на доставку одной единицы продукции, объём заказа и количество продукции, хранящейся на каждом складе :

Таблица тарифов на перевозку продукции и объёмов запасов на складе и заказов :

Магазин   Склад	“Булоч-ная”	“Хлеб”	“Сла- дос- ти”	“Сдо-ба”	“Сладко- ежка”	Запасы на складе (ед.прод)
“Крекер”	2,5	4	1	3	1,5	40
“Славянка”	3,5	2	3	1,6	4	55
“Сластёна”	0	1	2,5	2	1	25
Объём заказа (ед.прод)	20	50	40	30	50

 

Вариант № 10 .

Необходимо решить транспортную задачу: минимизировать расходы на доставку продукции заказчикам со складов фирмы, учитывая следующие затраты на доставку одной единицы продукции, объём заказа и количество продукции, хранящейся на каждом складе :

Таблица тарифов на перевозку продукции и объёмов запасов на складе и заказов :

 

 

Магазин   Склад	“Диана”	ГУМ	ЦУМ	“Прага”	“Елена”	Запасы на складе (ед.прод)
“Перово”	2	3	1,5	2	1	50
“Волжская”	5	6	4	5	0	80
“Пражская”	3	2	2,5	3	3,5	50
“Беговая”	1	3,5	1	0	1,5	60
Объём заказа (ед.прод)	30	50	50	40	25

 

Вариант № 11 .

Необходимо решить транспортную задачу: минимизировать расходы на доставку продукции заказчикам со складов фирмы, учитывая следующие затраты на доставку одной единицы продукции, объём заказа и количество продукции, хранящейся на каждом складе :

Таблица тарифов на перевозку продукции и объёмов запасов на складе и заказов :

Магазин   Склад	Москва	Тверь	Санкт-Петербург	Саратов	Запасы на складе (ед.прод)
Москва	0	1	1,5	3	50
Екатеринбург	5	3	5	2	30
Саратов	3	2,5	4	0	35
Вологда	2	2	3	2	40
Объём заказа (ед.прод)	40	50	25	30

 

Вариант № 12 .

Необходимо решить транспортную задачу: минимизировать расходы на доставку продукции заказчикам со складов фирмы, учитывая следующие затраты на доставку одной единицы продукции, объём заказа и количество продукции, хранящейся на каждом складе :

 

Таблица тарифов на перевозку продукции и объёмов запасов на складе и заказов :

Магазин   Склад	“Сумки”	“Мода”	“Анна”	“Галан-терея”	Запасы на складе (ед.прод)
Выхино	1	0	2	2,5	25
Арбатская	3	2,5	1,4	2	30
Каховская	2	1	4	3	40
Сокол	1,7	3	3,5	0,5	50
Объём заказа (ед.прод)	20	15	30	25

 

Вариант № 13.

Необходимо решить транспортную задачу: минимизировать расходы на доставку продукции заказчикам со складов фирмы, учитывая следующие затраты на доставку одной единицы продукции, объём заказа и количество продукции, хранящейся на каждом складе :

Таблица тарифов на перевозку продукции и объёмов запасов на складе и заказов :

Магазин   Склад	“Канц. товары”	“Школь-ник”	“Детский мир”	“Учебные принадлеж-ности	Запасы на складе (ед.прод)
Смоленская	1,5	2	0,5	3	25
Митино	0,5	4	3	2,5	20
Перово	3	1	2	0	30
Калужская	2	0,5	1,5	1	10
Объём заказа (ед.прод)	10	20	30	15

 

Вариант № 14 .

Необходимо решить транспортную задачу: минимизировать расходы на доставку продукции заказчикам со складов фирмы, учитывая следующие затраты на доставку одной единицы продукции, объём заказа и количество продукции, хранящейся на каждом складе :

Таблица тарифов на перевозку продукции и объёмов запасов на складе и заказов :

Заказчик   Склад	Типогра-фия №2	“Школь-ник”	“Детский мир”	“Книги”	Запасы на складе (ед.прод)
Рижская	2	1,5	0	0,5	25
Фили	1	2	3	1	65
Выхино	3	0,5	1	2,5	15
Объём заказа (ед.прод)	20	30	15	22

 

Вариант № 15 .

Необходимо решить транспортную задачу: минимизировать расходы на доставку продукции заказчикам со складов фирмы, учитывая следующие затраты на доставку одной единицы продукции, объём заказа и количество продукции, хранящейся на каждом складе :

Таблица тарифов на перевозку продукции и объёмов запасов на складе и заказов :

Магазин   Склад	“Свадебный салон”	ГУМ	ЦУМ	“Салон для новобрачных”	Запасы на складе (ед.прод)
Динамо	0	1	0,5	2	25
Сокольники	2	3	2	1	15
Кусково	3	2	1	0,5	10
Объём заказа (ед.прод)	15	20	15	10

 

Вариант № 16 .

Необходимо решить транспортную задачу: минимизировать расходы на доставку продукции заказчикам со складов фирмы, учитывая следующие затраты на доставку одной единицы продукции, объём заказа и количество продукции, хранящейся на каждом складе :

Таблица тарифов на перевозку продукции и объёмов запасов на складе и заказов :

Магазин Склад	“Мужская одежда”	“Руслан”	ГУМ	“Элита”	Запасы на скла-де (ед.прод)
Профсоюзная	1	3	2	2,5	20
Каховская	2	0,5	1,5	3	35
Семёновская	4	2	3	0	40
Пражская	3,5	1,5	3	1	15
Объём заказа (ед.прод)	30	20	25	15

 

Литература

1. Акулич И.Л. Математическое программирование в примерах и задачах. – М.: Высш. Шк., 1986

2. Костевич Л.С. Математическое программирование: Информ. технологии оптимальных решений. – Мн.: Новое знание, 2003

 

Лабораторная работа № 6

Тема: Задачи нелинейного программирования и их решение средствами Excel.

Программное обеспечение: Microsoft Excel

Основные сведения

При решении многих экономических задач и других задач наиболее полный и точный учет зависимостей между факторами и показателями, влияющими на критерий эффективности и ограничения, приводит к построению нелинейных экономико-математических моделей. Например, при формировании оптимальной производственной программы предприятия по критерию затрат учитывается себестоимость единицы продукции, которая уменьшается при увеличении объема выпускаемой продукции и приводит к нелинейному критерию эффективности.

В математических моделях нелинейных оптимизационных задач, называемых задачами нелинейного программирования, целевая функция и ограничения являются нелинейными функциями. Модель остается нелинейной и в случае если только целевая функция нелинейна, а ограничения – линейны, или наоборот – хотя бы одно из ограничений нелинейно, а целевая функция линейна.

В общем виде, математическая модель нелинейной задачи программирования формулируется следующим образом. Необходимо найти такой вектор n неизвестных , который доставляет максимум (или минимум) целевой функции , т.е.

и удовлетворяет системе ограничений

В отличие от задач линейного программирования, для задач нелинейного программирования не существует общего метода, позволяющего решать любые оптимизационные нелинейные задачи. Это обусловлено тем, что в задачах нелинейного программирования область допустимых решений может быть невыпуклой, а целевая функция может достигать экстремума не только на границе, но и внутри области допустимых решений системы ограничений. Кроме того, нелинейная целевая функция может иметь несколько локальных экстремумов, среди которых необходимо найти глобальный. В общем случае, ни один из существующих методов не гарантирует определение глобального экстремума.

Вместе с тем, некоторые типы задач нелинейного программирования хорошо изучены и для них существуют методы определения глобального экстремума. К таким задачам можно отнести классические задачи оптимизации без ограничений или с ограничениями-равенствами, у которых отсутствуют условия неотрицательности и дискретности переменных, целевая функция и функции в ограничениях непрерывны, имеют непрерывные частные производные по крайней мере второго порядка.

Особое место среди задач нелинейного программирования занимают выпуклые задачи, у которых область допустимых ограничений и целевая функция являются выпуклыми или вогнутыми. К таким задачам относятся, в частности, задачи квадратичного программирования, для которых характерно то, что целевая функция и/или ограничения являются функциями своих аргументов, в степени не выше второй. Наиболее важной характеристикой выпуклых (вогнутых) моделей нелинейного программирования является то, что для них локальный экстремум обязательно является и глобальным экстремумом.

Ниже рассматриваются только выпуклые (вогнутые) задачи нелинейного программирования.

 

 

Пример решения задачи нелинейного программирования с использованием Excel.

 

Задача. Предприятие может выпускать два вида продукции (j = 1, 2). На ее изготовление расходуется три вида ресурсов (i = 1, 2, 3). С учетом брака расход ресурсов на единицу производимой продукции j-го вида определяется выражением , а прибыль в зависимости от объемов производства равна , где – искомый объем производства продукции j-го вида; – норма расхода i-го ресурса на производство единицы продукции j-го вида; – коэффициент изменения расхода соответствующего ресурса с учетом выпуска бракованных изделий; – прибыль от реализации единицы продукции j-го вида; – коэффициент изменения прибыли, влияющий на объем производства продукции j-го вида. Требуется найти такие объемы производства продукции, при которых прибыль была бы максимальной.

Численные исходные данные приведены в таблице:

Ресурс	Нормы расхода ресурсов ( ) на продукцию вида j		Запас ресурса		Коэффициент изменения норм расхода ресурсов ( ) на продукцию вида j
	1	2			1	2
1	15	18	1350		0,1	0,05
2	12	16	1400		0,2	0,2
3	17	14	1580		0,1	0,15
Прибыль за ед. продукции	100	120
Коэффициент изменения прибыли	– 0,08	– 0,1

 

 

Математическая модель

Целевая функция, которую необходимо максимизировать равна

Максимум целевой функции находится при ограничениях

Математическую модель приведем к виду, пригодному для использования в Excel. После раскрытия скобок получаем

 

Решения задачи средствами Microsoft Excel

Вызовите Microsoft Excel.