
Cosmology. The Origin and Evolution of Cosmic Structure - Coles P., Lucchin F
..pdf
138 Phase Transitions and Inflation
F 1
T > Tc
2
T < Tc
Φ
Figure 7.1 Free energy F of a system which undergoes a spontaneous symmetry breaking at a phase transition of second order in the order parameter Φ. The minimum of curve 1, corresponding to a temperature T > Tc, represents the equilibrium disordered state; the transition occurs at T = Tc; one of the two minima of curve 2, corresponding to the temperature T < Tc, represents the equilibrium ordered state which appears after the transition.
is called the latent heat of the phase transition. One would have this type of transition if, for example, in Equation (7.3.1) one added an extra term γ(Φ2)3/2, with γ < 0, to the right-hand side. We now have the type of behaviour represented in Figure 7.2: in this case F acquires two new minima which become equal or less than F0 = F(0) for T Tc.
In first-order phase transitions, when T changes from the situation represented by curve 1 of Figure 7.2 to that represented by curve 3, the phenomenon of supercooling can occur: the system remains in the disordered state represented by Φ = 0 even when T < Tc (state A); this represents a metastable equilibrium. As T decreases further, or the system is perturbed by either internal or external fluctuations, the system rapidly evolves into state B, which is energetically stable, liberating latent heat in the process. The system, still in the ordered state, is heated again up to a temperature of order Tc by the release of this latent heat, a phenomenon called reheating.
7.4 Cosmological Phase Transitions
The model of spontaneous symmetry breaking has been widely applied to the behaviour of particle interactions in the theories outlined in Section 7.2. Because phase transitions of this type appear generically in the early Universe according to standard particle physics models, the initial stages of the Big Bang are often described as the era of phase transitions. One important idea, which we shall refer to later, is that we can identify the order parameter Φ with the value of some scalar quantum field, most importantly the Higgs field at GUT scales, and the free energy F can then be related to the e ective potential describing the interactions of that field, V(Φ). We shall elaborate on this in Sections 7.7 and 7.10.

Cosmological Phase Transitions |
139 |
|
F |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|||
|
|
|
T > |
|
T |
c |
|
|
|
|||||||||
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
2 |
||||||||||||
|
|
|
|
|
|
T |
|
|
|
|
|
|
|
|||||
|
A |
|
|
|
|
|
= T |
|
c |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
3 |
||||||||
T < |
T |
c |
||||||||||||||||
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B
Φ
Figure 7.2 Free energyF of a system which undergoes a spontaneous symmetry breaking at a phase transition of first order in the order parameter Φ. The absolute minimum of curve 1, corresponding to a temperature T > Tc, represents the equilibrium disordered state; the transition does not happen at T = Tc (curve 2), but at T < Tc, when the barrier between the central minimum and the two others becomes negligible (curve 3).
The period from tP 10−43 s, corresponding to a temperature TP 1019 GeV, to the moment at which quarks become confined in hadrons at T 200–300 MeV, can be divided into various intervals according to the phase transitions which characterise them.
1.TP 1019 GeV > T > TGUT 1015 GeV. In this period quantum gravitational e ects become negligible and the particles are held in thermal equilibrium for T 1016 GeV by means of interactions described by a GUT. Thanks to the fact that baryon number is not conserved in GUTs, any excess of baryons over antibaryons can be removed at high energies; at T 1015 GeV the Universe is baryon-symmetric, i.e. quarks and antiquarks are equivalent. It is possibly also the case that viscosity e ects at the GUT scale can lead
to a reduction in the level of inhomogeneity of the Universe at this time. At temperatures TGUT 1015 GeV, corresponding to t 10−37 s, we will take the simplest GUT symmetry of SU(5).
2.T 1015 GeV. At T 1015 GeV there is a spontaneous breaking of the SU(5) symmetry into SU(3) × SU(2) × U(1) or perhaps some other symmetry for some intervening period. As we shall see in detail later, the GUT phase transition at TGUT results in the formation of magnetic monopoles: this is a problem of the standard model which is discussed in Section 7.6 and which may be solved by inflation, which is usually assumed to occur in this epoch. A GUT which unifies the electroweak interactions with the strong interactions, puts leptons and hadrons on the same footing and thus allows processes which do not conserve baryon number B (violation of baryon number conservation
140 Phase Transitions and Inflation
is not allowed in either QCD or electroweak theory). It is thought therefore that processes could occur at TGUT, which might create a baryon–antibaryon asymmetry which is observed now in the form of the very large ratio nγ/nb, as we explained in Section 5.5. In order to create an excess of baryons from a situation which is initially baryon-symmetric at T > 1015 GeV, i.e. to realise a process of baryosynthesis, it is necessary to have
(a)processes which violate B conservation;
(b)violation of C or CP symmetry (C is charge conjugation; P is parity conjugation; violation of symmetry under these operations has been observed in electroweak interactions), otherwise, for any process which violates B-conservation, there would be another process with the same rate happening to the anti-baryons and thus cancelling the net e ect;
(c)processes which do violate B-conservation must occur out of equilibrium because a theorem of statistical mechanics shows that an equilibrium distribution with B = 0 remains so regardless of whether B, C and CP are violated – this theorem shows that equilibrium distributions cannot be modified by collisions even if the invariance under time-reversal is violated.
It is interesting to note that the three conditions above, necessary for the creation of a baryon–antibaryon asymmetry, were given by Sakharov (1966). It seems that these conditions are valid at T 1015 GeV, or slightly lower, depending on the particular version of GUT or other theory; it is even the case that baryosynthesis can occur at much lower energies, around the electroweak scale. Even though this problem is complicated and therefore rather controversial, with reasonable hypotheses one can arrive at a value of baryon–antibaryon asymmetry of order 10−8–10−13, which includes the observed value: the uncertainty here derives not only from the fact that one can obtain baryosynthesis in GUTs of various types, but also that in any individual GUT there are many free, or poorly determined, parameters. It is also worth noting that, if the Universe is initially lepton-symmetric, the reactions which violate B can also produce an excess of leptons over antileptons (equal in the case of SU(5) GUTs to that of the baryons over the antibaryons). This is simply because the GUTs unify quarks and leptons: this is one theoretical motivation for assumption, which we shall make in the next chapter: that the chemical potential for the leptons is very close to zero at the onset of nucleosynthesis. Notice finally that in a GUT the value of the baryon asymmetry actually produced depends only on microphysical parameters; this means that, even if the Universe is inhomogeneous, the value of the asymmetry should be the same in any region. Given that it is proportional to the entropy per baryon σrad, it turns out that any inhomogeneity produced must be of adiabatic type (i.e. leaving σrad unchanged relative to an unperturbed region). In some very special situations, which we shall not go into here, it is possible however to generate isothermal fluctuations. We shall discuss adiabatic and isothermal perturbations in much more detail in Chapter 12.
Problems of the Standard Model |
141 |
3.TGUT > T > TEW. When the temperature falls below 1015 GeV, the unification of the strong and electroweak interactions no longer holds. The superheavy bosons rapidly disappear through annihilation or decay processes. In the moment of symmetry breaking the order parameter Φ, whose appearance signals the phase transition proper, can assume a di erent ‘sign’ or ‘direction’ in adjoining spatial regions: it is possible in this way to create places where Φ changes rapidly with spatial position, as one moves between different regions, similar to the ‘Bloch walls’ which, in a ferromagnet, separate the di erent domains of magnetisation. These ‘singular’ regions where Φ is discontinuous have a structure which depends critically upon the symmetry
which has been broken; we shall return to this in Section 7.6. The period we are discussing here lasts from tGUT 10−37 s to tEW 10−11 s: in logarithmic terms this is a very long time indeed. It is probable that phase transitions occur in this period which are not yet well understood. This corresponds to an energy range from 100–1015 GeV; within the framework of the SU(5) model discussed above there are no particles predicted to have masses in this range of energies, which is, consequently, called the ‘grand desert’. Nevertheless, there remain many unresolved questions regarding this epoch. In any case, towards the end of this period one can safely say that, to a good approximation, the Universe is filled with an ideal gas of leptons and
antileptons, the four vector bosons, quarks and antiquarks and gluons; in all this corresponds to g 102. At the end of this period the size of the cosmological horizon is around one centimetre and contains around 1019 particles.
4.TEW > T > TQH 200–300 MeV. At T 102 GeV there will be a spontaneous breaking of the SU(2) × U(1) symmetry, through a phase transition which is probably of first order but very weakly so. All the leptons acquire masses
(with the probable exception of the neutrinos) while the intermediate vector bosons give rise to the massive bosons W+, W− and Z0 and photons. The massive bosons disappear rapidly through decay and annihilation processes when the temperature falls below around 90 GeV. For a temperature TQH 200–300 MeV, however, we have a final phase transition in the framework of QCD theory: the strong interactions do indeed become very strong and lead to the confinement of quarks into hadrons, the quark–hadron phase transition. There thus begins the (very short) hadron era, which we shall dis-
cuss in the next chapter. When the temperature reaches TQH, the cosmological time is tQH 10−5 s and the cosmological horizon is around a kilometre in size.
7.5 Problems of the Standard Model
The standard model of the hot Big Bang is based on the following assumptions.
1.That the laws of physics which have been verified at the present time by laboratory experiments are also valid in the early Universe (this does not
142 Phase Transitions and Inflation
include such theories as GUT, supersymmetry and the like which we refer to as ‘new physics’) and that gravity is described by the theory of general relativity without a cosmological constant.
2.That the Cosmological Principle holds.
3.That the appropriate ‘initial conditions’, which may in principle be predicted
by a more general theory, are that the temperature at some early time ti is such that Ti > 1012 K and the contents of the Universe are in thermal equilibrium, that there is (somehow) a baryon asymmetry consistent with the observed value of σrad, that Ω(ti) is very close to unity (see below), and, finally, that there is some spectrum of initial density fluctuations which give rise to structure formation at late times.
This standard cosmology has achieved four outstanding successes:
1.the predictions of light-element abundances produced during cosmological nucleosynthesis agree with observations, as we shall see in the next chapter;
2.the cosmic microwave background is naturally explained as a relic of the initial ‘hot’ thermal phase;
3.it accounts naturally for the expansion of the Universe; and
4.it provides a framework within which one can understand the formation of galaxies and other cosmic structures.
There remain, however, certain problems (or, at least, unexplained features) connected with the Big Bang cosmology:
1.the origin of the Universe or, in less elevated language, the evolution of the Universe before the Planck time;
2.the cosmological horizon, which we discuss below;
3.the question of why the Universe is close to being flat, again discussed below;
4.the baryosynthesis or, in other words, the origin of the baryon asymmetry;
5.the evolution of the Universe at energies greater than T > 100 GeV;
6.the origin of the primordial spectrum of density fluctuations, whatever it is;
7.the apparently ‘excessive’ degree of homogeneity and isotropy of the Universe; and
8.the nature of the ubiquitous dark matter.
Notice that there are, apparently, more ‘problems’ than ‘solutions’!
The incorporation of ‘new physics’ into the Big Bang model holds out the possibility of resolving some of these outstanding issues, though this has so far only been achieved in a qualitative manner. The assumptions made in what one might call the ‘revised standard model’ would then be that
1.known physics and theories of particle physics (‘new physics’) are valid, as is general relativity with Λ not necessarily zero;

The Monopole Problem |
143 |
2.the Cosmological Principle is valid; and
3.the same initial conditions hold as in the standard model at Ti 1019 GeV, except that the baryon asymmetry is accounted for (in principle) by the new physics we have accepted into the framework.
Successes of the ‘revised standard model’ are
1.all the advantages of the standard model;
2.a relatively clear understanding of the evolution of the Universe at T > 1012 K;
3.the possible existence of non-baryonic particles as candidates for the dark matter;
4.the explanation of baryosynthesis (though, as yet, only qualitatively); and
5.a consolidation of the theory of structure formation by virtue of the existence of non-baryonic particles through (3).
This modernised version of the Big Bang therefore eliminates many of the problems of the standard model, particularly the fourth, fifth and eighth of the previous list, but leaves some and, indeed, adds some others. Two new problems which appear in this model are concerned with: (1) the possible production of magnetic monopoles and (2) the cosmological constant. We shall discuss these in Sections 7.6 and 7.7. We shall see later in this chapter that the theory of inflation can ‘solve’ the monopole, flatness and horizon problems.
7.6 The Monopole Problem
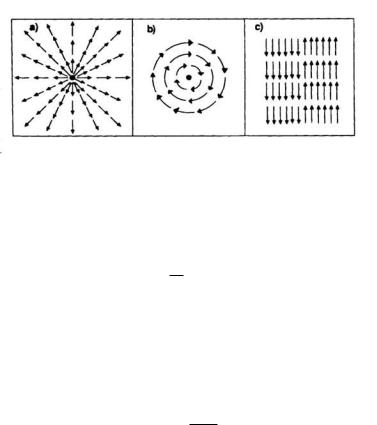
Any GUT in which electromagnetism, which has a U(1) gauge group, is contained within a gauge theory involving a spontaneous symmetry breaking of a higher symmetry, such as SU(5), provides a natural explanation for the quantisation of electrical charge and this implies the existence of magnetic monopoles. These monopoles are point-like defects in the Higgs field Φ which appears in GUTs. Defects are represented schematically in Figure 7.3, in which the arrows indicate the orientation of Φ in the internal symmetry space of the theory, while the location of the arrows represents a position in ordinary space. Monopoles are zero dimensional; higher-dimensional analogues are also possible and are called strings (one dimensional), domain walls (two dimensional) and textures (three dimensional).
In this discussion we shall use electrostatic units. Monopoles have a magnetic charge
gn = ngD, |
(7.6.1) |
which is a multiple of the Dirac charge gD,
gD = |
c |
= 68.5e; |
(7.6.2) |
2e |
144 Phase Transitions and Inflation
|
(a) |
(b) |
(c) |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Figure 7.3 Schematic representation of topological defects in the Higgs field: a monopole (a); a string (b); a domain wall (c). The three-dimensional analogue of these defects is called a texture, but we cannot draw this in two dimensions! The arrows represent the orientation of the field Φ in an internal symmetry space, while their position indicates location in real space.
a mass
c |
|
mM 4π e2 mX 103mX, |
(7.6.3) |
where X is the boson that mediates the GUT interaction, called the Higgs boson, with mass
mX e( c)1/2mGUT 10−1mGUT |
(7.6.4) |
(mGUT is the energy corresponding to the spontaneous breaking of the GUT symmetry); the size of the monopoles is
|
|
rM mXc . |
(7.6.5) |
For typical GUTs, such as SU(5), we have mGUT 1014–1015 GeV, so that mM 1016 GeV ( 10−8 g) and rM 10−28 cm.
The other types of topological defects in the Higgs field shown in Figure 7.3 are also predicted by certain GUTs. The type of defect appearing in a phase transition depends on the symmetry and how it is broken in a complicated fashion, which we shall not discuss here. From a cosmological perspective, domain walls, if they exist, represent a problem just as monopoles do and which we shall discuss a little later. Cosmic strings, however, again assuming they exist, may be a solution rather than a problem because they may be responsible for generating primordial fluctuations which give rise to galaxies and clusters of galaxies, though this is believed only by a minority of cosmologists; we shall discuss this option briefly in Section 13.9.
Now let us explain the cosmological monopole problem. In the course of its evolution the Universe su ers a spontaneous breaking of the GUT symmetry at TGUT, for example via SU(5) → SU(3)×SU(2)×U(1). As we discussed in Section 7.3 it therefore moves from a disordered phase to an ordered phase characterised by an order parameter Φ ≠ 0, which in this case is just the value of the Higgs field. During this transition monopoles will be formed. The number of monopoles can

The Cosmological Constant Problem |
145 |
be estimated in the following manner: if ξ is the characteristic dimension of the domains which form during the breaking of the symmetry (ξ is also sometimes called the correlation length of the Higgs field), the maximum number density of monopoles nM,max is of the order ξ−3. In reality, not all the intersections between domains give rise to monopoles: one expects that this reduces the above estimate by a factor p 101 . Given that the points within any single domain are causally connected, we must have
ξ < rH(t) 2ct 0.6g (T)−1/2 |
TPc |
, |
(7.6.6) |
|||||
kBT2 |
||||||||
where TP is the Planck temperature. It turns out therefore that, at TGUT, |
|
|||||||
|
GUT 1/2 |
T |
GUT |
3 |
|
|
|
|
|
|
|
|
|
||||
nM > p |
g (T ) |
|
nγ(TGUT), |
(7.6.7) |
||||
0.6TP |
|
|
||||||
which, for TGUT 1015 GeV, gives |
|
|
|
|
|
|
|
|
|
nM > 10−10nγ. |
|
|
|
(7.6.8) |
|||
Any subsequent physical processes are expected to be very ine cient at reducing the ratio nM/nγ. The present density of monopoles per unit volume is therefore expected to be
n0M > 10−10n0γ n0b, |
(7.6.9) |
which is of order, or greater than, that of the baryons and which corresponds to a density parameter in monopoles of order
mM |
Ωb 1016, |
|
ΩM > mp |
(7.6.10) |
clearly absurdly large.
The problem of the domain walls, in cases where they are predicted by GUTs, is of the same character. The problem of cosmological monopole production, which to some extent negates the successes of cosmologies incorporating the ‘new physics’, was the essential stimulus which gave rise to the inflationary cosmology we shall discuss later in this chapter.
7.7 The Cosmological Constant Problem
As we saw in Chapter 1, the Einstein equations with Λ ≠ 0, having
Tij(Λ) = −pΛgij + (pΛ + ρΛc2)UiUj, |
(7.7.1) |
||||
where |
|
|
|
|
|
ρΛ = − |
pΛ |
|
Λc2 |
|
|
|
≡ |
|
, |
(7.7.2) |
|
c2 |
8πG |
||||
146 Phase Transitions and Inflation
yield for the case of a homogeneous and isotropic universe the relations
a˙2 = 38 πG(ρ + ρΛ)a2 − Kc2, |
(7.7.3 a) |
||||
a¨ = − |
4 |
πG ρ + 3 |
p |
− 2ρΛ a. |
(7.7.3 b) |
3 |
c2 |
||||
From these equations at t = t0, putting p0 0, we obtain
K |
|
H02 |
|
|
|
= |
|
(Ω0 + ΩΛ − 1), |
(7.7.4 a) |
a02 |
c2 |
|||
|
q0 = 21 Ω0 − ΩΛ, |
(7.7.4 b) |
||
where ΩΛ ≡ ρΛ/ρ0c. The observational limits on Ω0 and q0 yield
|
|
|
|
|
|
|
|
|
m4 |
|
|
|
|
|
|ρΛ| < |
2 |
ρ0c |
|
4 |
× |
10−29 g cm−3 |
|
10−46 |
n |
|
10−48 |
GeV4 |
(7.7.5) |
|
( /c)3 |
||||||||||||||
|
|
|
|
|
|
|
(mn is the mass of a nucleon; in the last relation we have used ‘natural’ units in which = c = 1), corresponding to
|Λ| < 10−55 cm−2. |
(7.7.6) |
From Λ one can also construct a quantity which has the dimensions of a mass
|
|
3 |
|
1/4 |
|
3 |
1/4 |
|
|
mΛ = |ρΛ| |
|
|
|
|
= |
|
|Λ| |
< 10−32 eV |
(7.7.7) |
c |
|
8πGc |
(to be compared with the upper limit on the mass of the photon: according to recent estimates this is mγ < 3 × 10−27 eV). The problem of the cosmological constant lies in the fact that the quantities |Λ|, |ρΛ| and |mΛ| are so amazingly and, apparently, ‘unnaturally’ small.
The modern interpretation of Λ is the following: ρΛ and pΛ represent the density and pressure of the vacuum, which is understood to be like the ground state of a quantum system:
ρΛ ≡ ρv, pΛ ≡ pv = −ρvc2 |
(7.7.8) |
(the equation of state pv = −ρvc2 comes from the Lorentz-invariance of the energy–momentum tensor of the vacuum). In modern theories of elementary particles with spontaneous symmetry breaking it turns out that
ρv V(Φ, T), |
(7.7.9) |
where V(Φ, T) is the e ective potential for the theory. This is the analogous quantity to the free energy F discussed above in the simple (non-quantum) thermodynamical case of Section 7.3; its variation with T determines the spontaneous breaking of the symmetry; Φ is the Higgs field, the expectation value of which

The Cosmological Horizon Problem |
147 |
is analogous to the order parameter in the thermodynamical case. An important consequence of Equation (7.7.9) is that the cosmological ‘constant’ depends on time through its dependence upon T. This fact is essentially the basis of the inflationary model we shall come to shortly.
Modern gauge theories predict that
ρv |
m4 |
|
( /c)3 + const., |
(7.7.10) |
where m is the energy at which the transition occurs (1015 GeV for GUT transitions, 102 GeV for the electroweak transition, 10−1 GeV for the quark–hadron transition and (perhaps) 103 GeV for a supersymmetric transition). The constant in Equation (7.7.10) is arbitrary (although its value might be accounted for in supersymmetric theories). In the symmetry-breaking phase one has a decrease of ρv of order
∆ρv |
m4 |
|
( /c)3 , |
(7.7.11) |
corresponding to 1060 GeV4 for the GUT, 1012 GeV4 for supersymmetry, 108 GeV4 for the electroweak transition, and 10−4 GeV4 for QCD.
In light of these previous comments the cosmological constant problem can be posed in a clearer form:
ρv(tP) = ρv(t0)+ i |
∆ρv(mi) 10−48 GeV4 +1060 GeV4 = i |
∆ρv(mi)(1+10−108), |
|
|
(7.7.12) |
where ρv(tP) and ρv(t0) are the vacuum density at the Planck and present times, respectively, and mi represents the energies of the various phase transitions which occur between tP and t0. Equation (7.7.12) can be phrased in two ways: ρv(tP) must di er from i ∆ρv(mi) over the successive phase transitions by only one part in 10108; or the sum i ∆ρv(mi) must, in some way, arrange itself so as to satisfy (7.7.12). Either way, there is definitely a problem of extreme ‘fine-tuning’ in terms of ρv(tP) or i ∆ρv(mi).
At the moment, there exist only a few theoretical models which even attempt to resolve the problem of the cosmological constant. Indeed, many cosmologists regard this problem as the most serious one in all cosmology. This is strictly connected with the theory of particle physics and, in some way, to quantum gravity. Inflation, we shall see, does not solve this problem; indeed, one could say that inflation is founded upon it.
7.8 The Cosmological Horizon Problem
7.8.1 The problem
Recall that one of the fundamental assumptions of the Big Bang theory is the Cosmological Principle, which, as we explained in Chapter 6, is intimately connected
