Теорема про єдиний розв'язок рівнянь електродинаміки.

Розглянемо для внутрішніх задач електродинаміки: маємо об'єм V, обмежений поверхнею S. Теорема говорить: розв'язок рівняння електродинаміки для об'єму V, обмеженого поверхнею S, буде єдиним при наступних умовах:

1. В початковий момент часу t = 0 вектори поля і однозначно задані в межах всього об'єму V.

2. На протязі всього часу від 0 до t на поверхні S задані однозначно або , або .

- на частині поверхні S₁

- на частині поверхні S₂

Тобто розв'язок, який ми отримаємо згідно з цими умовами буде єдиний.

Доведення від супротивного:

нехай існують 2 розв'язки цієї задачі:

, і ,

Так як ми маємо лінійне середовище (тобто працює принцип суперпозиції), то рівнянням Максвела повинні задовольняти не тільки ці 2 розв'язки, а й будь-яка їх комбінація.

Розглянемо комбінацію поля , :

Для цього третього рішення:

а) відсутні сторонні струми ;

б) в момент t = 0 і задані однозначно, а значить , а значить :

; ; (при t = 0)

в) на поверхні S поля і дорівнюють нулю. Фізично це означає, що через цю поверхню енергія не проходить:

,

Застосуємо до третього розв'язку теорему Пойнтінга, згідно з якою зменшення енергії електромагнітного поля іде на:

(бо );

, бо проекція

, бо проекція

Залишилось:

- потужність переходу електромагнітної енергії в теплову (це швидкість переходу). Цей процес незворотній, тобто: (завжди).

Розглянемо :

1. в момент t = 0 

2. а далі , тобто пришли до протиріччя.

Тому залишається тільки те, що:

,

тобто на протязі всього проміжку від 0 до t:

А це значить, що:



Отже довели теорему.

Для зовнішніх задач електродинаміки: задані струми в обмеженому об'ємі V.

Задаємо однозначно поля в початковий момент часу, потім всю область, де існують струми, обмежуємо поверхнею S радіуса R :

1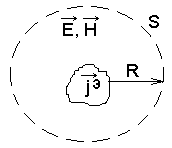 ) t = 0 : ,

2) На протязі часу  0  t  : при умові, що R, а швидкість поширення електромагнітної енергії скінчена (швидкість світла) і завжди на поверхні , і ця теорема зводиться до внутрішньої теореми (попередньої).

Поляризація електромагнітних хвиль.

Електромагнітні хвилі можуть бути як поляризовані так і неполяризовані.

Неполяризовані - це такі, в яких напрямок вектора в кожну мить часу невизначений (змінюється хаотично), (світлові промені, космічне випромінювання).

Поляризовані - це такі, в яких ми можемо визначити в кожну мить часу напрямок вектора .

Поляризація визначається напрямком вектора .

При поширенні електромагнітних хвиль вектори і будуть перпендикулярні до напрямку поширення хвилі, а вектор співпадає з поширенням хвилі.

Кут між площиною поляризації і площиною землі називається кутом поляризації :

Площина поляризації - це площина, яка задається векторами і .

В иди поляризації:

1. Лінійна поляризація : міняється величина , але не змінюється напрямок в просторі (так само і век вектор ).

Годограф вектора для лінійної поляризації це пряма лінія.

В площині це буде синусоїда (розподіл вектора ).

Вектор .

- фазова швидкість (якщо  і  дійсні величини):

- при розгляданні з часом t картинка зміщується вправо з швидкістю .

с - швидкість світу

Якщо  і  - комплексні величини:

; ;

т о розподіл в загальному випадку буде такий ( змінюється по cos , буде зсунутий по фазі - або запізнення, або випередження):

Вектор Пойнтінга на одних ділянках буде протилежний координаті Z , а на інших - співпадати, тобто це будуть пульсації енергії.

Р озглянемо, що буде на поверхні провідника: вектор Пойнтінга буде направлений вздовж лінії передачі. В середині провідника вектор Пойнтінга має дві складові, і ми будемо мати перетворення енергії в теплову. Вектор буде направлений в середину провідника.

Розподіл вектора :

Б лижче до поверхні провідників потік вектора Пойнтінга буде більшим.

Епюри розподілу вектора Пойнтінга:

Я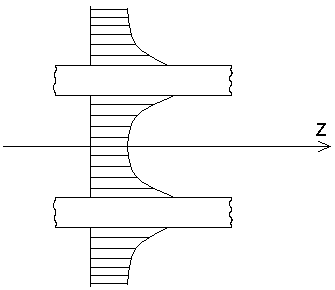 кщо кути будуть однаковими, то фаза буде нуль:

Якщо магнітні і електричні втрати будуть різними, то фаза буде або - або +.

Відносно поверхні Землі поляризація може бути різна (це і для лінійної і для еліптичної поляризації).

Н априклад, вертикальна поляризація (перпендикулярно до поверхні):

Горизонтальна поляризація: в цьому випадку вібратори можемо поставити горизонтально до землі (для телебачення):

Н а ділянці 1 - сумарне випромінювання  0, бо відстань між провідниками мала. А на ділянці 2 - є випромінювання.

Може бути похила поляризація:

Кругова поляризація:

в кожній точці простору вектори і змінюють свій напрямок, але не змінюють величину. Годографом є коло, яке повторюється з періодом:

Вектор при поширенні може обертатись або по часовій стрільці або проти (лівий чи правий гвинт).

Г одографом вектора в просторі є спіраль по циліндру. (В залежності який гвинт по напрямку поширення - маємо ліву і праву поляризацію):

3) Еліптична поляризація: змінюється як величина, так і напрямок і .

Годографом є еліпс (може бути права або ліва поляризація).

Вона може бути похилою, вертикальною і горизонтальною (в залежності від напрямку).

Коефіцієнт еліптичності:

В ектор в просторі поширюється по поверхні еліптичного циліндра.

В лінійній поляризації :

В круговій поляризації :

Є антени, які випромінюють електромагнітні хвилі з круговою поляризацією. Наприклад, спіральна антена:

М ожна отримати кругову поляризацію синтезом з двох лінійних поляризаторів.

В ектор при - різниця фаз (робиться фазообертачами) (права кругова поляризація); при - ліва кругова поляризація.

Кругову поляризацію можна отримати з двох лінійних хвиль при умовах:

1. кут в просторі 90 (між площинами поляризації);

2. амплітуди однакові (інакше буде еліптична поляризація);

3. різниця фаз дорівнює ;

Всі інші випадки приведуть до появи еліптичної поляризації.

З двох хвиль з круговою поляризацією можна отримати хвилю з лінійною поляризацією, якщо:

1. вони мають однакову амплітуду;

2. крутяться в протилежних напрямках;

Якщо амплітуди рівні, а фази різні, то ми можемо сумарну поляризацію двох кругових поляризацій крутити в просторі як ми хочемо (міняти кут нахилу, міняючи різницю фаз між круговими хвилями).

Задача1: випромінювання елементарного електронного випромінювача.

Будемо розв'язувати безпосередньо рівняння Максвела:

Маємо два рівняння з двома невідомими і розв'язок буде у вигляді системи. Треба знайти розподіл електричного і магнітного поля і .

Повинно бути задано : розподіл струмів, ₀, , ₀, , .

Для спрощення задачі вводимо векторні електродинамічні потенціали:

- векторний потенціал електричних струмів;

- векторний потенціал магнітних струмів.

Треба знайти поля через потенціали (без викладок)

()

, - поки що нам не відомі.

()

Якщо замість і в рівняння Максвела підставити ці і , то після всіх операцій ми отримаємо два окремих незалежних рівняння:

- рівняння Гельмгольца

k - хвильове число : ;

 - фазова постійна ;

 - постійна згасання електромагнітної хвилі.

Далі задача зводиться до окремого розв'язку двох диференційних рівнянь.

Рівняння і - це система неоднорідних диференційних рівнянь Гельмгольца.

Т епер постановка задачі зводиться до такої: маємо об'єм V, в якому задані струми і треба знайти потенціали або в деякій точці просторі на відстані r :

Запишемо загальний розв'язок цих рівнянь :

k - хвильовий вектор :

- довжина елементарного вібратора.

Наша антенна система може бути Т - подібна, розподіл струму в ній буде нерівномірний, і нам потрібно буде інтегрувати по всьому об'єму, зайнятому струмом. Ми будемо знаходити поле в якійсь точці як суперпозицію полів від кожного елементарного випромінювача, на які ми розбили нашу Т - подібну антену. Але ми будемо розглядати окремі задачі для простих елементарних випромінювачів ( ).

Першим елементарним випромінювачем буде провідник, в якому електричний струм розподілений рівномірно .

В ибираємо сферичну систему координат.

Центр системи в середині провідника :

Д алі необхідно знайти векторний потенціал електричних струмів, знаючи розподіл струму, тобто розв'язати рівняння Гельмгольца :

При тих допущеннях, які ми зробили (рівномірний розподіл струму), цей розв'язок легко знайти виносячи струм за знак інтегралу :

Припущення : ; (елементарний вібратор настільки малий, що координата {від вібратора до точки} >>довжини вібратора).

Тоді :

- момент струму

Знайдемо потенціал магнітних струмів : бо

Розпишемо в сферичній системі координат, вздовж координати Z :

(проекція на площину XOY - це точка)

Підставивши це у () і () :

Всі інші складові магнітного поля = 0

Електричне поле буде мати 2 складові:

Це все буде в сферичній системі координат. Задача розв'язана. Ми отримали загальний розв'язок.

Розглянемо цей розв'язок біль детально. Залежності від кута  тут нема, від кута є залежність: або cos або sin. А залежність від r відбувається по різних законах . Множник означає, що електромагнітне поле існує у вигляді поширення електромагнітних хвиль з якоюсь фазою : - фазовий множник.

А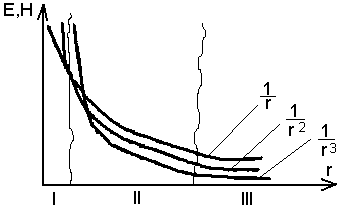 мплітуда змінюється по законам : .

Намалюємо ці залежності:

Можна спростити ці вирази, розбивши координату r на 3 зони :

I - ближня зона :

при  = 0 (втрат немає) :

Це значить, що (при цьому ) ;

в цьому випадку :

- магнітне поле в ближній зоні навколо обмеженого провідника з струмом (якщо б провідник був нескінченно великий, то була б залежність не , а ).

Т.ч. ми отримали закон Біо-Савара-Лапласа для стаціонарного магнітного поля короткого провідника.

Це електричне поле електричного диполя, тобто електростатичне поле двох зарядів (закон зміни , якщо б у нас був один заряд, то ми мали б закон ).

Тобто ми маємо для електричного диполя закон Біо-Савара-Лапласа, який є законом Кулона.

Різниця фаз між H і E 90, так як в знаменнику стоїть j. Тобто, якщо електричне поле максимальне то нема і навпаки.

С ереднє значення вектора Пойнтінга за період :

( )

Тут ми маємо реактивну (коливальну) енергію в першій зоні :

H  jE

Перша зона - це зона індукції.

Друга зона - це зона, де всі значення поля мають приблизно однакові амплітуди (тому треба зберігати всі члени ), тобто використовуємо такі формули :

III зона - дальня зона : , тобто .

В цьому випадку всіма членами, що змінюються по закону і , можна знехтувати.

І залишаються тільки ті поля, що змінюються по закону .

В цьому випадку :

і ми не пишемо.

Перепишемо ці поля по іншому :

[Ом]

Можна ще більше спростити ці формули підставивши

(1)

Таким чином, поле в дальній зоні має тільки дві складові : і . Будемо їх розглядати:

Маємо диполь :

У нас E і H змінюються синфазно : E  H

Середнє за період значення вектора Пойнтінга показує потужність переходу цього процесу через поверхню S, тобто потужність випромінювання:

Тепер дослідимо формули (1) : не залежать від , а залежать від . Побудуємо графік залежності поля від кута  :

при  = 0 випромінювання нема ;

при  = 90 максимальне випромінювання.

Таким чином в полярній системі координат це коло :

В ид збоку :

В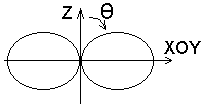 ид зверху (в площині XOY):

В просторі (в аксонометрії ) це буде тороїд :

- це діаграма спрямованості антени.

Вона характеризує інтенсивність випромінювання - по напрямках. Вздовж провіднику випромінювання не буде, а максимальне випромінювання буде поперек провідника :

З найдемо вектор Пойнтінга :

Потужність випромінювання на одиницю площини змінюється по закону .

Таким чином діаграма антени по потужності :

В здовж координати Z вектор Пойнтінга = 0 .

Знайдемо потужність, що випромінюється антеною :

Порівнявши ці формули знайдемо вираз для R_В :

- це опір випромінювання (це не опір провідника), він залежить від хвильового опору середовища Z і від .

При =1 , =1 : Z=120 , тоді :

Ц е формули для розрахунку R_В і P_В у вільному просторі, їх можна застосовувати тільки при l <<  (тобто можемо користуватися ними для електричних диполів).

Опір випромінювання R_В ми поміряти в антені не можемо, але ми можемо в антені поміряти R опір, тоді :

- потужність, яка поглинається в антені.

Антена буде характеризуватися коефіцієнтом корисної дії (ККД) :

д е :

Для  ККД, треба  і  R.

Ще один параметр антени : у нас є така діаграма спрямованості антени, у цієї антени є потужність випромінювання P_В, вздовж осі Z випромінювання = 0. Далі, випромінювання у гіпотетичної антени однакове в усі сторони : у цієї ізотропної антени є потужність випромінювання Р_{вип.із.ан.}

Т ому вводять коефіцієнт спрямованої дії (КСД):

при умові, що максимум напруженості в дальній зоні обох антен однаковий:

Для елементарного диполя Д  1.5, але може бути 10000 для релейних станцій.

Задача2: Випромінювання елементарного магнітного випромінювача.

Постановка задачі: маємо магнітний провідник довжиною , по якому тече магнітний струм (маємо магнітний диполь).

Необхідно знайти напруженість поля в дальній зоні .

Розв'язувати задачу будемо таким же чином як і раніше.

З гідно з принципом переставної подвійності рівнянь цей розв'язок можна записати відразу.

- направлений на нас.

- для дальнього розв'язку (для дальньої зони)

Робимо такі заміни :

Замість буде:

- без змін

Замість буде:

Тепер подивимось, що буде зі знаками:

Це і є розв'язок.

Знайдемо опір випромінювання і потужність випромінювання.

Раніше у нас було :

Провідність випромінювання магнітної антени:

Потужність:

- вимірюється в Вольтах (видно з формули Р_В).

Де протікає магнітний струм:

1. є рамка з і магнітний струм буде  рамці прямо в повітрі (це магнітний диполь):

Перехід від до :

;

2. є площина, в якій прорізана

щілина і по поверхні щілини

тече магнітний струм: 3)