Вектор Пойнтінга в комплексній формі.
Для миттєвих
значень:
Через комплексні амплітуди:
Нас цікавить середнє за період значення вектора Пойнтінга, розглянемо вирази з експонентою:
(це
коливальна енергія) = 0 - за період.
Тепер розглянемо те що залишилося:
- середнє за період
значення вектора Пойнтінга.
Або:
Для комплексних амплітуд:
- середнє за період
значення вектора Пойнтінга (вважаючи,
що E
і H
комплексні амплітуди).
Основні електродинамічні задачі.
Більшість практичних задач електродинаміки зводиться до декількох абстрактних.
Класифікація задач:
Задача аналізу: задана конфігурація, геометричні розміри і параметри матеріалу електродинамічної системи. Знайти розподіл електромагнітного поля в кожній точці системи.
Задача синтезу: задано розподіл електромагнітного поля. Знайти конфігурацію, геометричні розміри і параметри матеріалу електродинамічної системи (це обернена задача аналізу).
Аналіз - це однозначна задача. Задача синтезу не однозначна.
В свою чергу задачі аналізу поділяються на внутрішні і зовнішні:
Внутрішня задача: задано розподіл електричних і магнітних струмів. Знайти розв'язок рівняння Максвела в об'ємі V обмеженому замкненою поверхнею S. Цей розв'язок повинно задовольняти крайовим умовам на поверхні S (аналоги коливальних систем, резонатори).
Зовнішня задача:
задано розподіл електричних і магнітних
струмів в деякому обмеженому об'ємі.
Знайти розподіл електромагнітного поля
в нескінченому просторі, яке повинно
задовольняти умовам випромінювання на
нескінченності (це умова Зомерфельда,
яка зводиться до слідуючого: поля на
нескінченності повинні зменшуватися
по амплітуді по закону не менше ніж
(можна
)).
(Приклади: задачі дифракції, задачі випромінювання).
Методи розв'язку задач електродинаміки:
Аналітичні методи: розв'язок отримаємо у вигляді формули. Переваги: наглядність (бо є аналітична формула), легкість, простота розрахунку.
Недоліки: дуже вузьке коло задач, які можна розв'язати цим методом. Здебільшого це задачі, в яких проста конфігурація електродинамічних систем.
Чисельні методи розрахунку (для всіх інших задач).
При цьому диференційні рівняння зводяться до системи алгебраїчних лінійних рівнянь.
Переваги: широке коло задач, які можна розв'язати цим методом.
Недоліки: результатам, що одержані на електронному обчислювальному пристрої не можна довіряти (бо може виникнути велика похибка), тому цей розв'язок треба завжди перевіряти різними методами.
Області:
Є квазістаціонарна область:
L<<
Т
оді
вводиться додатковий параметр:
- хвильове число.
Далі ми розкладаємо в ряд по цьому параметру,
при
цьому електродинамічна задача зводиться
до квазістаціонарної задачі.
Приклад: котушка, випромінюванням можна знехтувати і буде тільки коливальний процес.
Резонансна область:
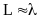
В цьому випадку треба з великою ступінню точності розв'язувати рівняння Максвела з крайовими умовами.
Методи, які використовуються: метод інтегральних перетворень, метод власних функцій.
Для спрощення розв'язку необхідно підібрати координати поверхні, які б співпадали з координатами системи.
Квазіоптична область:
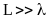
Тут може бути асимптотичне дослідження рівняння з резонансної області (коли 0).