Рівняння Максвела для комплексних амплітуд

Оскільки в рівняннях Максвела присутні похідні по часу, то будемо вважати, що всі електромагнітні процеси в електродинаміці змінюються в часі від - до +, тому E(t) і H(t) будуть змінюватися по закону sin або cos.

Т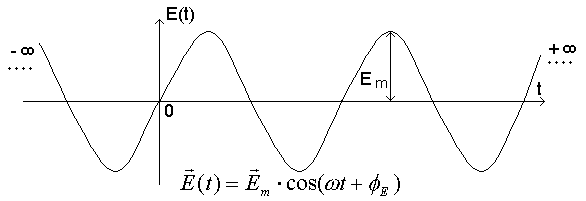 аким чином ми можемо розкласти і в ряд Фурь’є.

Переходимо від миттєвих значень і до їх комплексних амплітуд:

Тоді для переходу до миттєвих значень від комплексних амплітуд потрібно:

Аналогічно:

Тобто все змінюється по гармонійному закону:

Перше рівняння Максвела для комплексних амплітуд

- це для миттєвих значень.

Тепер підставимо сюди комплексні значення, і отримаємо:

- це похідні по координатам, не залежить від координат і експоненту можна винести за знак .

- const, від часу не залежить і її можна винести за знак і взяти похідну по t тільки від .

Тому маємо:

Остаточно рівняння Максвела для комплексних амплітуд:

Основна перевага методу комплексних амплітуд - нема похідної, а тільки множення на j.

Друге рівняння Максвела:

Третє рівняння:

Четверте рівняння:

Для матеріальних рівнянь:

- це число зв'язку

- комплексна провідність (є дійсна і уявна частини)

Звільнимося від зайвих індексів і будемо вважати:

це для комплексних амплітуд

І тепер рівняння Максвела мають вигляд:

(1)

(2)

Для однорідного ізотропного середовища у нас будуть не тензори, а скаляри. Підставимо у (1) і (2) всі інші рівняння. Спочатку у перше рівняння Максвела:

(3)

де: - сторонній струм

 - комплексні числа.

Якщо  - комплексне число, то пишемо "-" при умові, що пишемо ; а якщо пишемо , то пишемо "+" (це необхідна умова, якщо незробити заміну, то це буде порушенням принципу причинності).

Аналогічно для провідності:

(для або )

Формалізація завела нас до чотирьох параметрів речовини (в рівнянні (3)): ,

але ми будемо вважати, що в нас є ідеальний діелектрик в якому є електрони провідності. Вводимо еквівалентну діелектричну проникність:

- відповідає за поляризацію в діелектрику

- відповідає за втрати в діелектрику

В входять (так як і в і ):

Перепишемо рівняння (3):

- це вже деяка комплексна величина

- сюди теж входить дійсна та уявна частини

Друге рівняння Максвела:

 - без хвильки, тому що нема магнітних зарядів і струмів.

При наявності магнітних зарядів та струмів цю систему можна записати в такому вигляді:

(  )

- комплексна речовина

(  )

Тепер ці рівняння стають симетричними. Щоб отримати (  ) з (  ) треба зробити заміну:

(4)

Ми отримали принцип переставної подвійності рівнянь Максвела. Що цей принцип дає? Розв'язавши рівняння для електричних струмів ми можемо відразу записати розв'язок рівнянь для магнітних струмів, не розв'язуючи спочатку, а скориставшись принципом переставної подвійності (тобто заміною (4)).

Тепер розглянемо комплексне  :

На комплексній площині це має вигляд:

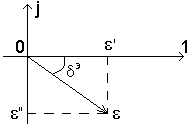- тангенс кута діелектричних втрат (залежить від частоти).

Діелектрик без втрат ( ):

Д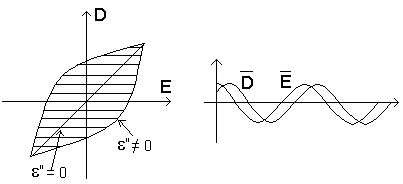 іелектрик з втратами ( ) - це еліпс. І ми маємо тут гістерезіс.

- характеризує втрати при поляризації діелектрика (площа еліпса).

Для магнітних матеріалів:

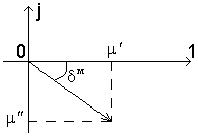- характеризує втрати на перемагнічування магнітного матеріалу.

Для води (t = 20C)

Д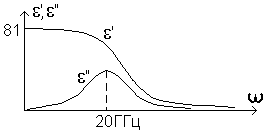 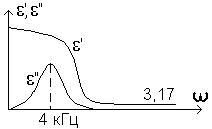ля льоду (t = -10C)

Для феритів, які застосовують в феритових антенах приймача.

Ц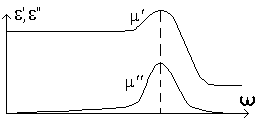 і характеристики наводяться в довідниках.