Енергія електромагнітного поля Вектор Пойтинга (теорема)

Ці формули не виводяться, вони є постулатами. Енергія, що запасається в електричному та в магнітне полі:

Розглянемо енергію, що зосереджується в конденсаторі; ця енергія знаходиться в електричному полі:

V – це весь об’єм, де існує електричне поле (тобто це ).

Тепер розглянемо магнітну енергію, що запасається в індуктивності:

(1)

Закон повного поля говорить, що:

l – довжина контуру;

L – індуктивність;

n – кількість витків;

(2)

;

Щоб знайти L треба розрахувати стаціонарне магнітне поле.

Теорема Пойнтінга: витікає з рівняння Максвела.

(1)

(2)

Помножимо (1) скалярно на , а (2) – на і віднімемо їх:

- це теорема Пойтінга у диф. формі.

Проінтегруємо по об’єму, тобто там, де існують ці поля:

Згідно з теоремою Остроградського-Гауса:

- це теорема Пойнтінга в інтегральній формі.

Щоб дати фізичний зміст, розглянемо кожний з цих інтегралів:

- вектор Пойнтінга – густина потоку електромагнітної енергії через площу поверхні S.

Потік електромагнітної хвилі через елемент поверхні :

- потужність випромінювання (може мати будь-який знак).

Розглянемо другий інтеграл:

(3)

- густина струму провідності.

З рівняння Максвела:

(4)

- напруженість електричного поля сторонніх джерел.

З рівняння (4): (5)

(5)(3):

- потужність переходу електромагнітної енергії в теплову.

- потужність сторонніх джерел.

Розглянемо третій інтеграл:

- зміна електромагнітної енергії.

Тепер, коли в теоремі Пойнтинга замінити кожний інтеграл, отримаємо:

- закон збереження електромагнітної енергії в інтегральній формі.

Розглянемо випадки, коли:

1. 

Ц е говорить про те, що в об’ємі V, обмеженому поверхнею S, відбувається зменшення енергії на: збудження сторонніх сил, випромінювання електромагнітної енергії, перетворення в теплову.

2. Нехай , тоді:

Тобто йде на випромінювання, нагрівання і зміну електромагнітної енергії. Таких випадків можна розглянути багато.

3)

Це площина, в якій є якась електромагнітна енергія.

Розглянемо, що з нею відбувається:

- провідність стінок;

- провідність в середині;

Р=0, Р_В=0, Р_СТ=0 і виходить, що

Тобто в середині відбувається перетворення (ідеальний коливальний контур (резонатор)) магнітної енергії в електричну і навпаки:

; .

Крайові умови електродинаміки

В они потрібні для розв’язку дифф. рівнянь.

Якщо розглядати будь-яке дифф. рівняння, в якому параметри речовини ( ) залежить від координати Z, то і поля будуть мінятися по такому закону. І похідні, які входять в дифф. рівняння, мають кінцеве значення.

Інший випадок, коли параметри речовини змінюються скачками. Тобто поля теж міняються скачками (E, H, Д, В). А значить і похідна має в цих точках (*) значення нескінченності.

Т ому, щоб зв’язати рівняння для (І) і (ІІ) потрібно мати крайові умови на межі поділу.

Крайові умови виведемо з рівнянь Максвела. Будемо вважати, що межа поділу (*) буде навколо координат Z₀(Z), тобто зміюється монотонно, але дуже швидко:

В цьому випадку вже нема розриву похідної, і рівняння Максвела можна розглядати для областей (І) і (ІІ) і Z.

Коли отримаємо результат, то візьмемо від нього границю: .

Задача 1: Наше середовище складається з двох середовищ.

Параметри І-го :

ІІ-го :

В кожному середовищі існують свої поля.

В першому електричне поле , в другому . Величина і напрямок поля задані, знайти .

Для цього розглянемо на нормальну і тангенціальну (породільну) складові: .

Розглянемо спочатку крайові умови для дотичних складових (розглянемо два ідеальних діелектрика: ).

В ибираємо на межі поділу якийсь контур інтегрування, щоб половина його проходила в 1-ому середовищі, а друга в другому. Х – вибираємо також малою, щоб в його межах поле суттєво не змінювалось. Відстань (1-2)= Z – ширина межі поділу.

Скористуємось другим рівнянням Максвела в інтегральній формі:

Розглянемо ці два інтеграла при умові, що:

Z0

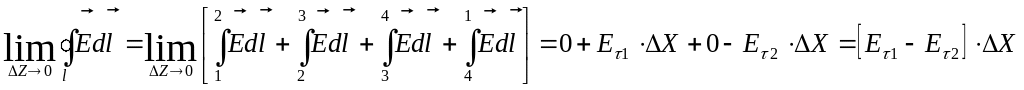
Тобто маємо:

Х – не нуль, ми його вибирали скінченим. Тоді нуль це те, що в дужках:

Отже, перша крайова умова для будь-яких середовищ:

- дотична складова вектора не змінюється при переході через межу поділу двох середовищ.

Тепер розглянемо нормальні складові:

Виберемо не контур, а поверхню інтегрування (площину), у якої половина в першому середовищі, а половина – в другому.

Спочатку розглянемо нормальні складові вектора : D_n1 i D_n2.

Вектори dS скрізь будуть  до площини. Зайдемо потік через замкнену поверхню:

Тобто в нашому випадку може бути об’ємний і поверхневий заряди:

Розглянемо перший інтеграл:

Розглянемо другий інтеграл:

Маємо:

- друга крайова умова:

Скачок нормальної складової вектора електричної індукції на межі поділу двох середовищ дорівнює густині поверхневого заряду.

Ц е можна зрозуміти наступним чином: маємо поверхню, на якій є додатній заряд (+), і прикладаємо поле :

Тоді в області (І) силові векторні лінії будуть додаватися (будуть густіші), а в області (ІІ) відніматись (будуть рідкіші):

Я кщо поверхня не заряджена (ідеальний діелектрик), то :

- якщо нема заряду на межі.

Р озглянемо крайові умови для дотичних складових вектора :

Беремо перше рівняння Максвела в інтегральній формі:

тут можуть протікати такі струми

- це нормаль (спрямований  до контуру вздовж межі поділу) – одиночний вектор по S

Перший інтеграл:

Другий інтеграл:

Тут при Z0, S0 і залишаємо тільки поверхневий струм, який тече на нас  до поверхні: (об’ємного струму нема).

- скачок дотичної складової вектора напруженості магнітного поля на межі поділу двох середовищ дорівнює густині поверхневого струму ( об’ємний струм на цей скачок не впливає).

А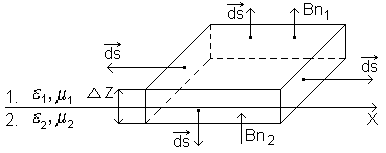 налогічно вектору розглянемо крайові умови для нормальних складових вектора магнітного поля :

Розглянемо такий інтеграл:

, бо магнітне поле зарядів ще не знайдено, а магнітні лінії замкнені.

Звідси знаходимо (бо S0):

- нормальна складова вектора магнітної індукції не змінюється при переході через межу поділу двох середовищ.

Якщо з матеріального рівняння підставити замість , то:

Випишемо в таблицю ці крайові умови:

В скалярній формі	В векторній формі

Розглянемо деякі випадки: нехай у нас є магнітні і електричні заряди, тоді є магнітний струм і рівняння Максвела можна записати таким чином:

- електричні заряди;

- магнітні заряди;

Рух дає електричний струм .Рух дає магнітний струм .

1)

2)

3)

4)

Рівняння стають симетричними, тоді крайові умови теж стають симетричними:

В електродинаміці застосовують таке поняття, як магнітний струм, і використовуються рівняння в симетричній формі.

Тобто, знайшовши розв’язок для електричного струму можемо не розв’язуючи задачі, а тільки враховуючи формулу симетрії, записати розв’язок для магнітного струму.

1. Якщо є провідник з електричним струмом:

Т о можемо еквівалентно ввести такий диполь з магнітним струмом, який буде еквівалентний рамці з електричним струмом:

2. В соленоїді:

Розглянемо окремі випадки крайових умов:

Перше середовище – ідеальний діелектрик, друге – ідеальний провідник.

1. 

2. 

При наявності малої різниці потенціалів між двома точками в ідеальному провіднику струм буде =. Але цього бути не може (між двома сусідніми точками не може бути потенціал, відмінний від нуля).

Тобто електричне поле не може існувати в середовищі ідеального провідника:

Тоді для цього випадку крайові умови:

- тобто вони тільки  до поверхні.

- тобто магнітні лінії підходять тільки готично до межі поділу.

- крайова умова в векторній формі.