Електродинаміка

Електродинаміка вивчає змінні електромагнітні поля.

До цього часу рівняння електродинаміки ми не виводили.

Почнемо з першого рівняння стаціонарного магнітне поля:

(10)

Знайдемо div обох частин:

Т обто: - тобто лінії струму завжди замкнені.

Це придатне для постійного струму:

В середині провідника:

Зовні:

Розглянемо чи придатні ці рівняння для змінного струму:

У цьому випадку:

Таким чином, рівняння (10) не годиться для змінних електромагнітних полів, так як ми отримали протиріччя (з математичного аналізу), що .

Спробуємо виправити це рівняння, тобто знайдемо div в колі змінного струму.

Струм який тече: (+)

Якщо візьмемо нижню обкладинку конденсатора і обмежимо її поверхнею S, то ми будемо мати об’єм V:

(*)

Струм по поверхні S:

(**)

Підставляємо (*) і (**) в (+):

Згідно з теоремою Остроградського-Гауса:

- закон збереження заряду або рівняння безперервності.

Підставимо в це рівняння значення з електростатики:

Звідси маємо:

- перше рівняння електродинаміки. (І)

Вихрове магнітне поле створюється струмом провідності і змінним за часом електричним полем.

Назвемо струмом зміщення.

В вакуумі, де існує , ніяких зарядів немає і тому в вакуумі це змінне за часом електро- магнітне поле.

Виникнення каже про існування вихрового поля (між обкладинками конденсатора):

У вакуумі:

В інтегральний формі:

Друге рівняння електродинаміки має вигляд:

його лишимо без змін.

Трете рівняння:

теж придатне, але треба розуміти чи буде статичне чи динамічне.

Розглянемо перше рівняння електростатики: (11)

В інтегральній формі:

Розглянемо замкнений провідниковий контур:

н ехай цей провідник знаходиться в змінному за часом магнітному полі. В цьому контурі виникає електрорушійна сила.

Якщо провідник розрізати, то на його кінцях виникає напруга:

; Ф – магнітний потік.

Тепер запишемо в диф. формі: потенціал це інтеграл по замкненому контуру:

Магнітне потік дорівнює інтегралу по поверхні S, що обмежена контуром:

Підставивши:

Тобто рівняння (11) не годиться для змінних полів.

По теоремі Стокса перейдемо до поверхневого інтегралу:

І отримаємо диф. форму:

- друге рівняння електродинаміки. (ІІ)

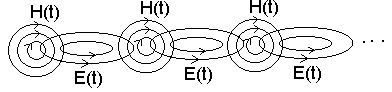
Вийшло так, що змінне електричне поле стало вихровим.

Причиною вихрового електричного змінного поля є змінне за часом магнітне поле (і навпаки).

Це справедливо для будь-якого контуру. Отже маємо І і ІІ закони Максвела.

Таким чином змінне електромагнітне поле поширюється в просторі з часом у вигляді змінних електромагнітних хвиль. Тобто має такий ланцюг:

Повна система рівнянь Максвела (рівнянь електродинаміки)

В диференційній формі	В інтегральній формі
1.	1.
2.	2.
Електричні векторні лінії починаються і закінчуються на заряді.	3. Потік вектора через замкнену поверхню дорівнює повному заряду, обмеженому цією поверхнею.
Магнітні лінії замкнені.	4.

Це неповна система, тому доповнимо її:

Матеріальні рівняння (які встановлюють зв’язок):

; - тензор провідності; - стороння сила.