Електростатичне поле в діелектрику
Діелектрик – це речовина, що не має вільних зарядів.
Під дією зовнішнього електричного поля діелектрик поляризується (додатній заряд зміщується в напрямку поля, а від’ємний навпаки).
Види поляризації:
Електронна (це не полярна поляризація).
2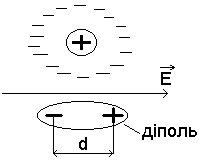
)
Іонна
(це не полярна поляризація).
3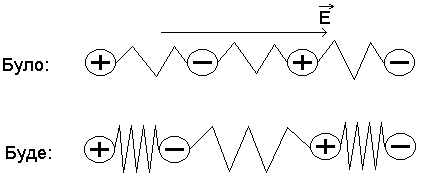
)
Поляризація
полярних діелектриків:
Орієнтаційна поляризація:
П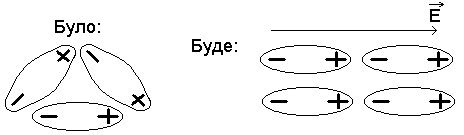
роцес
поляризації з часом відбувається по
експоненті:
N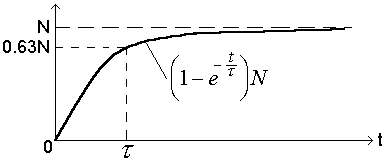
– кількість поляризованих молекул
-
час релаксації діелектрика (до 0.63N)
4) Спонтанна поляризація (в сегнетоелектриках) – ми маємо одиницю поляризованого об’єму, навіть при відсутності зовнішнього поля .
(Це теж полярний діелектрик)
Розглянемо полярну молекулу:
-
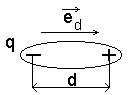
одиничний вектор по напрямку d.
Кожна
з таких молекул має дипольний
момент
:
- вона характеризує будь-який вид
полярізації.
Вектор поляризації речовини:
Розглянемо, як діє електростатичне поле в діелектрику:
Вносимо в середину об’єму V, обмеженого сферичною поверхнею S, заряд q. Під дією зовнішнього поля діелектрик поляризується:
З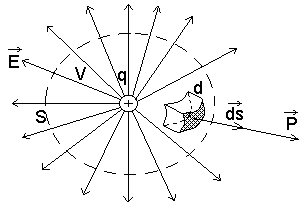
находимо
заряд, що перейшов через поверхню S:
Q’ – це заряд, розміщений в шарі товщиною d.
dQ’ – це заряд в об’ємі dV.
Щоб знайти весь заряд, треба проінтегрувати вектор поляризації речовини по замкненій поверхні S:
Позитивний заряд, який перейшов через поверхню S дорівнює Q’. В середині залишився заряд (-Q’). Тепер застосуємо теорему Гауса:
-
вектор
електричного зміщення (електростатичної
індукції).
Тоді теорема Гауса для заряду в діелектрику буде мати вигляд:
По теоремі Остроградського-Гауса:
-
теорема Гауса в диф. формі.
-густиа
вільних зарядів.
Вектор
полярізації діелектрика
- це є фукція електричного поля
:
Ця функція невизначена (тобто її потрібно дослідити до якогось певного часу t).
Можемо ввести класифікацію діелектриків:
Однорідна і неоднорідна залежність
Середовище називається однорідним, якщо його параметри не залежать від координат (тобто в кожній точці в середині ми маємо одну і ту ж функціональну залежність).
Середовище називається неоднорідним, якщо його параметри (функціональна залежність) залежать від координат.
2) Лінійна залежність – це лінійне середовище, параметри якого не залежать від величини поля.
Нелінійна залежність – це нелінійне середовище, параметри якого залежать від величини поля.
3
)
Середовище називають ізотропним,
коли його параметри не залежать від
напрямку електричного поля
.
Середовище називають анізотропним, коли його параметри залежать від напрямку електричного поля .
Приклад ізотропного середовища.
Приклад анізотропного середовища.
Математично це має вигляд:
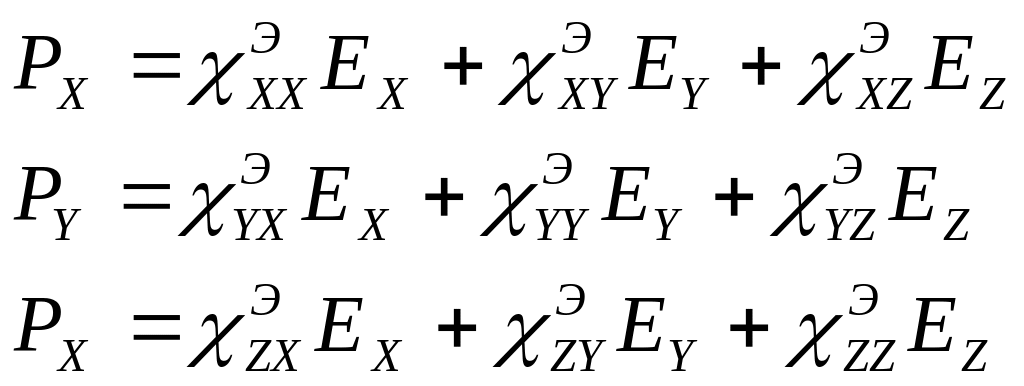
де індекс “Э” означає, що це стосується електричного поля. Тут записано, що вектори і не співпадають у просторі.
Для спрощення форми запису векторів і можна записати:
-
тензор електричного сприйняття середовища
(тензор другого рангу).
Якщо параметри середовища залежать від часу, то воно називається параметричним.
(4)
Вданому випадку, це тензор другого
рангу. Скаляр
– це тензор нульового рангу. Вектор
– це тензор першого рангу.
Кількість компонент в тензорі рахується по формулі (r-ранг): 3r.
Для скаляра: 30=1;
вектор: 31=3;
тензор 2-го рангу: 32=9.
Тензор 2-го рангу – це оператор, який ставить у відповідність одному вектору інший вектор (тобто це кількість комбінацій, за допомогою яких ми з одного вектора отримуємо інший).
Підставимо (4) в (3):
-
це оператор, який переводить вектор
сам в себе:
-
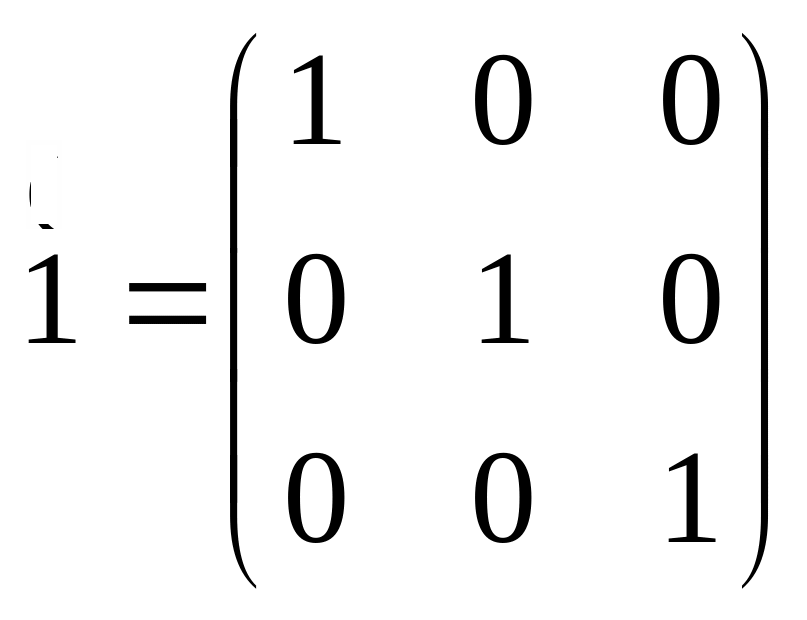
тензор електричної проникності.
Тобто
в загальному випадку вектори
і
не співпадають і записуються за
допомогою
:
Якщо
три координати:
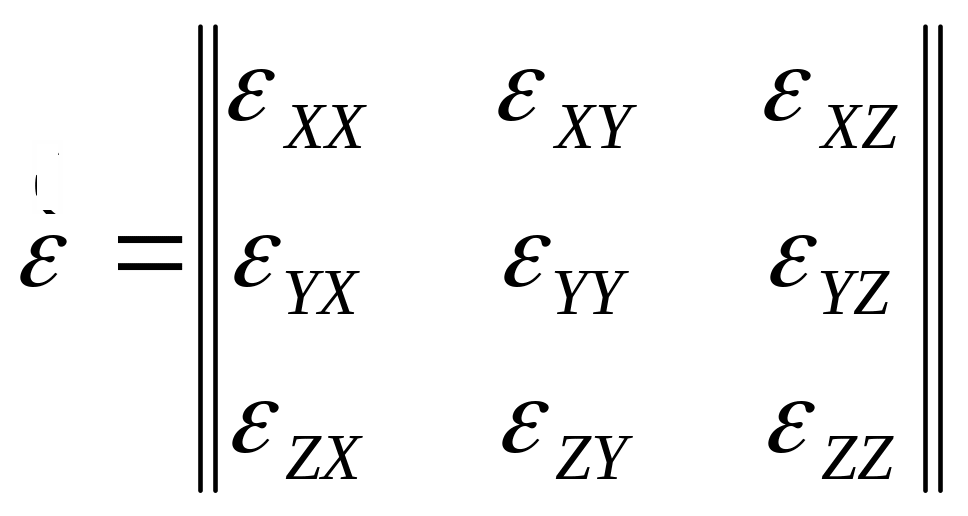
Випадки:
Для ізотропного діелектрика:
В довідниках можуть давати два значення
:
і
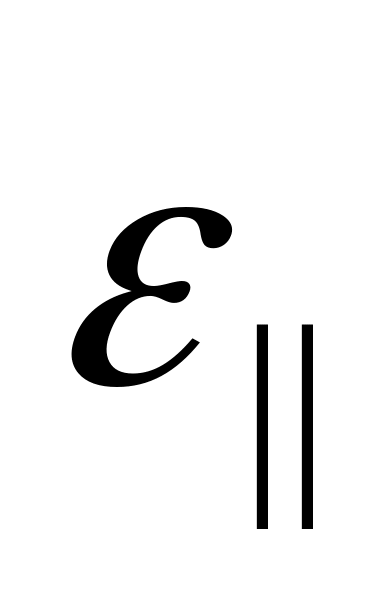.Вибором систем координат можна звести цей тензор до діагонального, але в діагоналі всі значення будуть різними.
Це анізотропні монокристали:
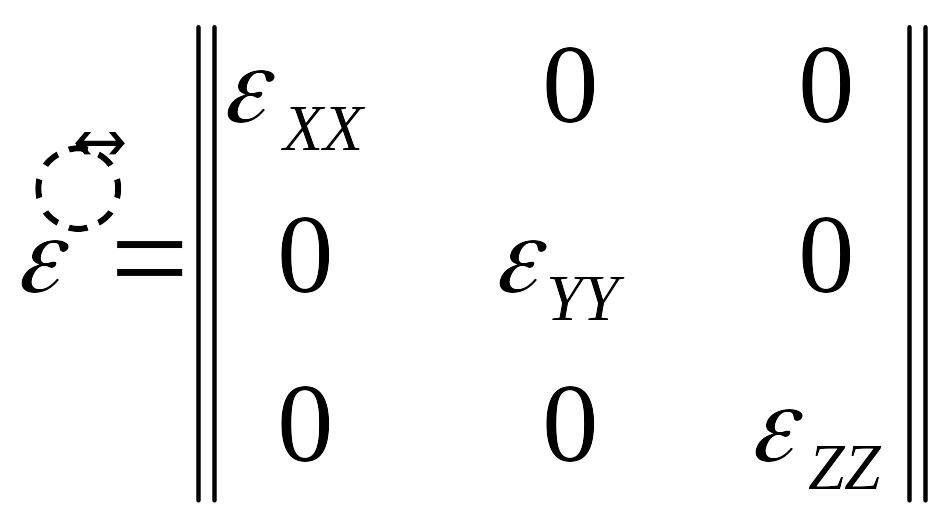
Для змінних електромагнітних полів тензор має вигляд:
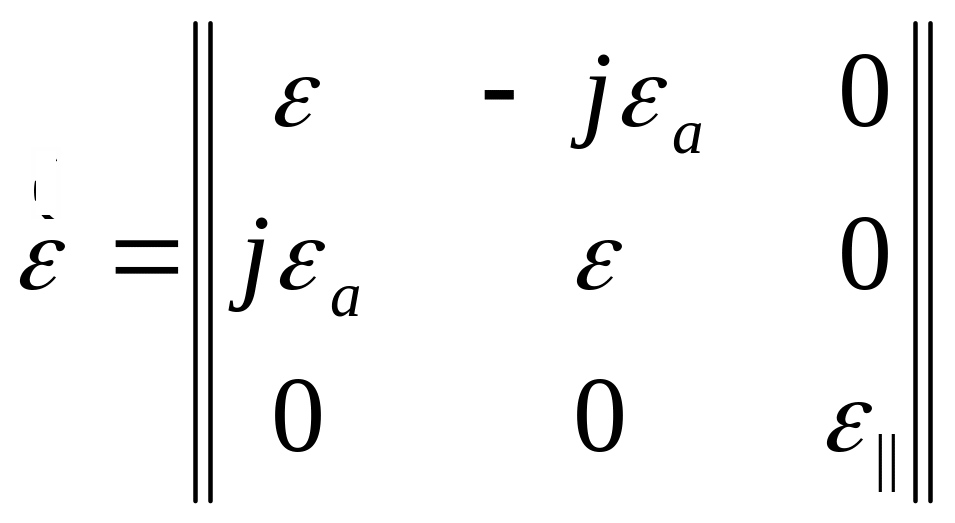
Ніяким вибором системи координат ми не можемо звести цей тензор до діагонального.
Такою матрицею описуються гіратропні середовища - це середовища, в яких можливий ефект Фарадея (в даному випадку це гіротропне середовище).
Приклад такого середовища – плазма навколо землі в присутності магнітного поля землі.